高中数学人教A版(2019)必修(第二册) 8.3.1棱柱棱锥棱台的表面积和体积课件(共28张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)必修(第二册) 8.3.1棱柱棱锥棱台的表面积和体积课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 00:00:00 | ||
图片预览





文档简介
课件28张PPT。8.3.1棱柱棱锥棱台的表面积和体积(1)矩形面积公式: __________。
(2)三角形面积公式:_________。
正三角形面积公式:_______。
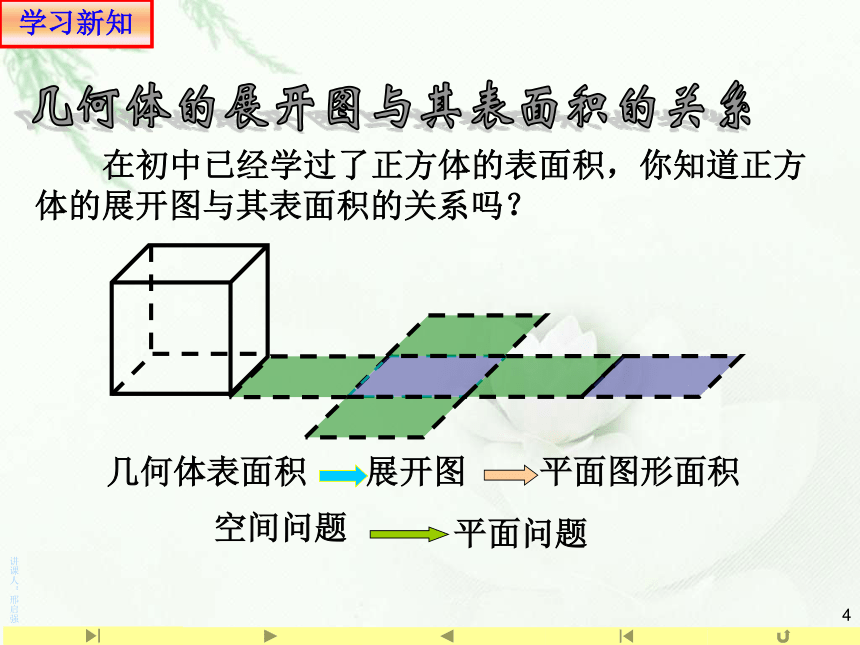
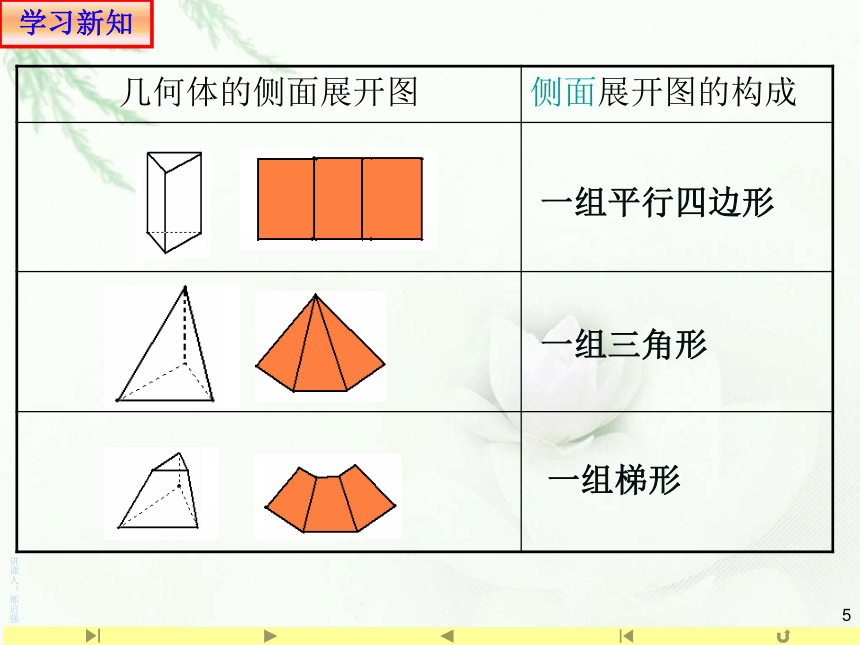
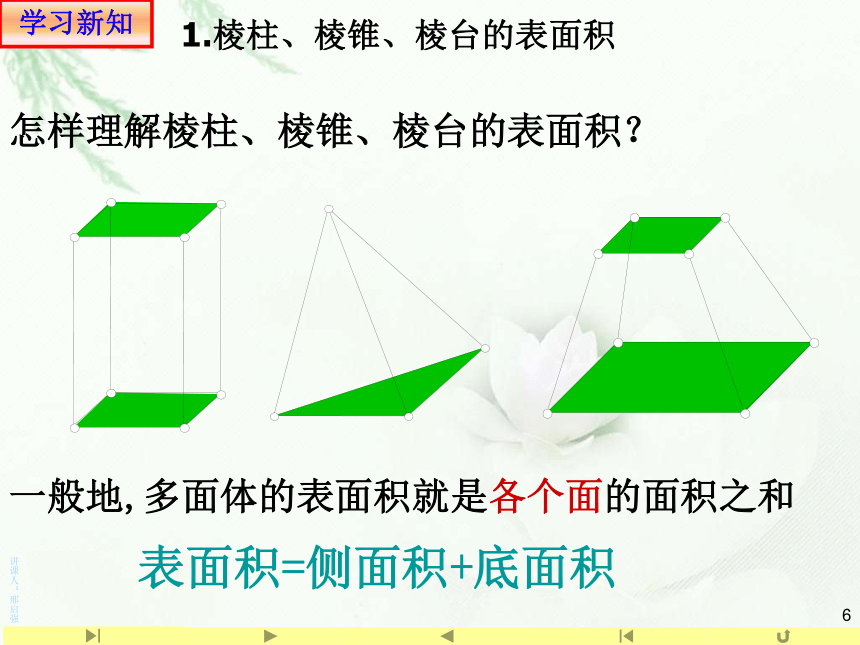
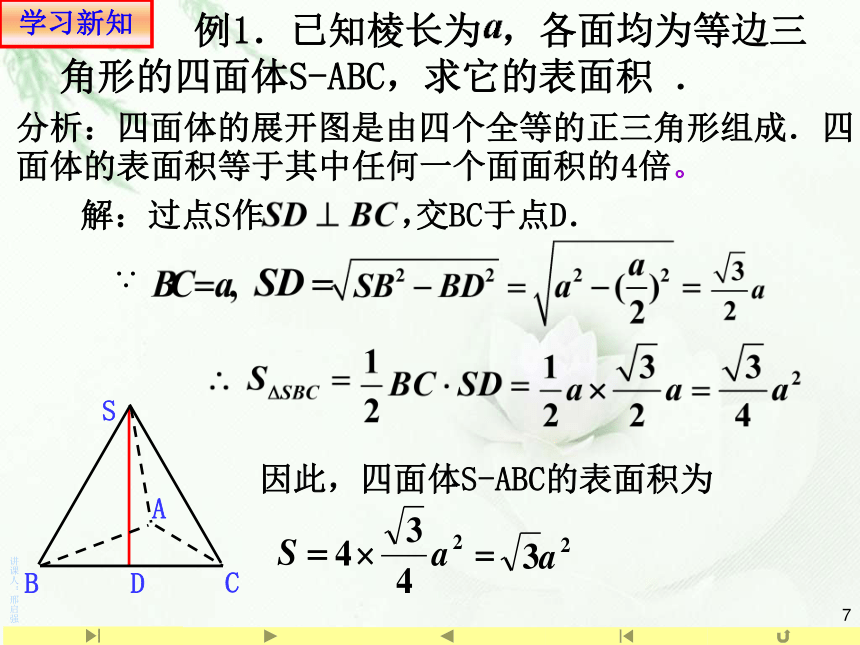
(6)梯形面积公式: __________复习引入(一)柱体、锥体、台体的表面积 思考:面积是相对于平面图形而言的,体积是相对于空间几何体而言的.面积:平面图形所占平面的大小 体积:几何体所占空间的大小 表面积:几何体表面面积的大小复习引入几何体的展开图与其表面积的关系 在初中已经学过了正方体的表面积,你知道正方体的展开图与其表面积的关系吗?几何体表面积学习新知一组平行四边形一组梯形一组三角形学习新知怎样理解棱柱、棱锥、棱台的表面积?一般地,多面体的表面积就是各个面的面积之和表面积=侧面积+底面积1.棱柱、棱锥、棱台的表面积学习新知分析:四面体的展开图是由四个全等的正三角形组成.四面体的表面积等于其中任何一个面面积的4倍。
因此,四面体S-ABC的表面积为学习新知【习练·破】
已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,则该四棱台的表面积为________.?长方体体积:正方体体积:体积:几何体所占空间的大小 学习新知(a,b,c分别是长方体的长、宽、高)一般地,如果棱柱的底面积是S,高是h,那么这个棱柱的体积V棱柱=Sh.棱柱的高是指两底面之间的距离,即从一底面上任意一点向另一个底面作垂线,这点与垂足(垂线与底面的交点)之间的距离关于体积有如下几个原理:
(1)相同的几何体的体积相等;
(2)一个几何体的体积等于它的各部分体积之和; (3)等底面积等高的两个同类几何体的体积相等; (4)体积相等的两个几何体叫做等积体.
学习新知学习新知 将一个三棱柱按如图所示分解成三个三棱锥,那么这三个三棱锥的体积有什么关系?它们与三棱柱的体积有什么关系? 推广到一般的棱锥,你猜想锥体的体积公式是什么? 如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍. 因此,一般地,如果棱锥的底面面积为S,高为h,那么该棱锥的体积学习新知棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.根据棱台定义,如何计算台体的体积?设棱台的上、下底面面积分别为S′和S,高为h,那么台体的体积公式是什么?学习新知棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足(垂线与底面的交点)之间的距离学习新知学习新知在棱台体体积公式中,若S′=S,S′=0,则公式分别变形为什么?学习新知典型例题例2一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少(精确到0.01m3)?分析:漏斗由两个多面体组成,其容积就是两个多面体的体积和.解:由题意知
V长方体ABCD-A'B'C'D'=1×1×0.5=0.5(m3),练习:已知有一正四棱台的上底边长为4cm,下底边长为8cm,高为3cm,
求其体积。巩固练习【例3】如图所示,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比. 【思维·引】先求出棱锥的体积,再求得剩余部分的体积,最后求得体积之比.1∶5【内化·悟】
怎样求几何体的体积?
提示:求几何体的体积,关键是弄清该几何体是柱体,锥体还是台体,再分别选择公式求解.【类题·通】
常见的求几何体体积的方法(1)公式法:直接代入公式求解.(2)等积法:如四面体的任何一个面都可以作为
底面,只需选用底面积和高都易求的形式即可.(3)分割法:将几何体分割成易求解的几部分,分别求体积.【习练·破】
如图所示,正方体ABCD-A1B1C1D1的棱长为a,过顶点B,D,A1截下一个三棱锥,则剩余部分的体积为________.?故剩余部分的体积V=角度1 等积变换法求体积
【例4】如图所示,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A-DED1的体积为________.?【思维·引】把三棱锥A-DED1转换为三棱锥E-DD1A,底面为直角三角形DAD1,高为正方体的棱长.【素养·探】
等积转换法是求锥体体积的常用方法,特别是当题目中某些点是不固定的点时,常用等积转换固定一个面,再进行求值.在解题过程中主要考查直观想象和数学运算的核心素养.变式:如图所示,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,求三棱锥D1-EDF的体积.角度2 等体积法求点到面的距离
【例5】如图,在棱长为a的正方体ABCD-A1B1C1D1中,求点A到平面A1BD的距离d. 【思维·引】先求出三棱锥A-BDA1的体积,再求出三角形BDA1的面积,再根据等体积法求点到平面的距离.各面面积之和小结:棱柱、棱锥、棱台棱柱、棱锥、棱台的表面积棱柱体积棱锥体积棱台体积常见的求几何体体积的方法(1)公式法:直接代入公式求解.(2)等积法:如四面体的任何一个面都可以作为
底面,只需选用底面积和高都易求的形式即可.(3)分割法:将几何体分割成易求解的几部分,分别求体积.2、选做题:课时跟踪检测二十二1、必做题:
完成学案导学P65——P67
8.3.1棱柱、棱锥、棱台的表面积和体积
作业
(2)三角形面积公式:_________。
正三角形面积公式:_______。
(6)梯形面积公式: __________复习引入(一)柱体、锥体、台体的表面积 思考:面积是相对于平面图形而言的,体积是相对于空间几何体而言的.面积:平面图形所占平面的大小 体积:几何体所占空间的大小 表面积:几何体表面面积的大小复习引入几何体的展开图与其表面积的关系 在初中已经学过了正方体的表面积,你知道正方体的展开图与其表面积的关系吗?几何体表面积学习新知一组平行四边形一组梯形一组三角形学习新知怎样理解棱柱、棱锥、棱台的表面积?一般地,多面体的表面积就是各个面的面积之和表面积=侧面积+底面积1.棱柱、棱锥、棱台的表面积学习新知分析:四面体的展开图是由四个全等的正三角形组成.四面体的表面积等于其中任何一个面面积的4倍。
因此,四面体S-ABC的表面积为学习新知【习练·破】
已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,则该四棱台的表面积为________.?长方体体积:正方体体积:体积:几何体所占空间的大小 学习新知(a,b,c分别是长方体的长、宽、高)一般地,如果棱柱的底面积是S,高是h,那么这个棱柱的体积V棱柱=Sh.棱柱的高是指两底面之间的距离,即从一底面上任意一点向另一个底面作垂线,这点与垂足(垂线与底面的交点)之间的距离关于体积有如下几个原理:
(1)相同的几何体的体积相等;
(2)一个几何体的体积等于它的各部分体积之和; (3)等底面积等高的两个同类几何体的体积相等; (4)体积相等的两个几何体叫做等积体.
学习新知学习新知 将一个三棱柱按如图所示分解成三个三棱锥,那么这三个三棱锥的体积有什么关系?它们与三棱柱的体积有什么关系? 推广到一般的棱锥,你猜想锥体的体积公式是什么? 如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍. 因此,一般地,如果棱锥的底面面积为S,高为h,那么该棱锥的体积学习新知棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.根据棱台定义,如何计算台体的体积?设棱台的上、下底面面积分别为S′和S,高为h,那么台体的体积公式是什么?学习新知棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足(垂线与底面的交点)之间的距离学习新知学习新知在棱台体体积公式中,若S′=S,S′=0,则公式分别变形为什么?学习新知典型例题例2一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少(精确到0.01m3)?分析:漏斗由两个多面体组成,其容积就是两个多面体的体积和.解:由题意知
V长方体ABCD-A'B'C'D'=1×1×0.5=0.5(m3),练习:已知有一正四棱台的上底边长为4cm,下底边长为8cm,高为3cm,
求其体积。巩固练习【例3】如图所示,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比. 【思维·引】先求出棱锥的体积,再求得剩余部分的体积,最后求得体积之比.1∶5【内化·悟】
怎样求几何体的体积?
提示:求几何体的体积,关键是弄清该几何体是柱体,锥体还是台体,再分别选择公式求解.【类题·通】
常见的求几何体体积的方法(1)公式法:直接代入公式求解.(2)等积法:如四面体的任何一个面都可以作为
底面,只需选用底面积和高都易求的形式即可.(3)分割法:将几何体分割成易求解的几部分,分别求体积.【习练·破】
如图所示,正方体ABCD-A1B1C1D1的棱长为a,过顶点B,D,A1截下一个三棱锥,则剩余部分的体积为________.?故剩余部分的体积V=角度1 等积变换法求体积
【例4】如图所示,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A-DED1的体积为________.?【思维·引】把三棱锥A-DED1转换为三棱锥E-DD1A,底面为直角三角形DAD1,高为正方体的棱长.【素养·探】
等积转换法是求锥体体积的常用方法,特别是当题目中某些点是不固定的点时,常用等积转换固定一个面,再进行求值.在解题过程中主要考查直观想象和数学运算的核心素养.变式:如图所示,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,求三棱锥D1-EDF的体积.角度2 等体积法求点到面的距离
【例5】如图,在棱长为a的正方体ABCD-A1B1C1D1中,求点A到平面A1BD的距离d. 【思维·引】先求出三棱锥A-BDA1的体积,再求出三角形BDA1的面积,再根据等体积法求点到平面的距离.各面面积之和小结:棱柱、棱锥、棱台棱柱、棱锥、棱台的表面积棱柱体积棱锥体积棱台体积常见的求几何体体积的方法(1)公式法:直接代入公式求解.(2)等积法:如四面体的任何一个面都可以作为
底面,只需选用底面积和高都易求的形式即可.(3)分割法:将几何体分割成易求解的几部分,分别求体积.2、选做题:课时跟踪检测二十二1、必做题:
完成学案导学P65——P67
8.3.1棱柱、棱锥、棱台的表面积和体积
作业
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
