七年级数学下册单元试卷-第二章《相交线与平行线》-北师大版(含答案)
文档属性
| 名称 | 七年级数学下册单元试卷-第二章《相交线与平行线》-北师大版(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 130.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-15 00:00:00 | ||
图片预览


文档简介
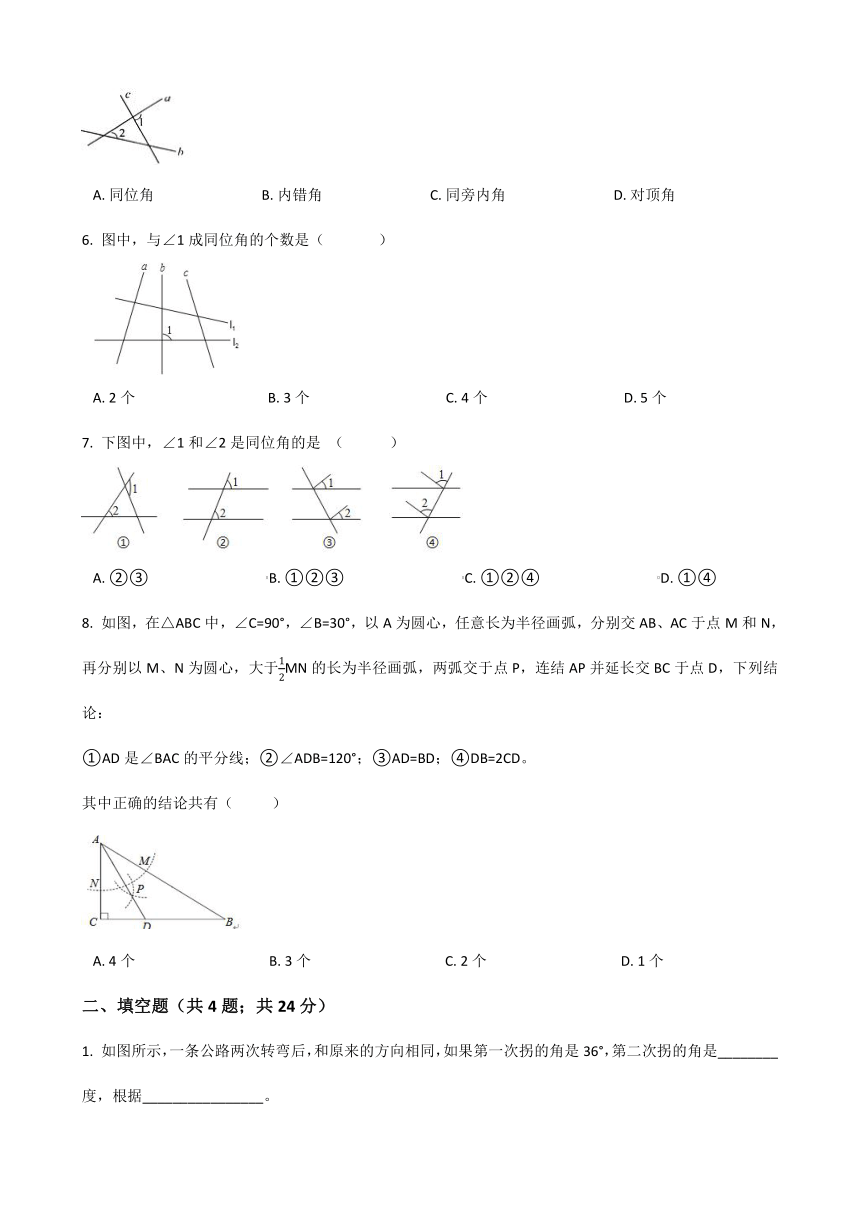
北师大版七年级数学下册单元试卷-第二章《相交线与平行线》
姓名: 班级: 座号:
一、单选题(共8题;共32分)
1. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度是(? ?? )
A.?第一次右拐50°,第二次左拐130°??????????????????????????B.?第一次左拐50°,第二次右拐50°
C.?第一次左拐50°,第二次左拐130°???????????????????????D.?第一次右拐50°,第二次右拐50°
2. 如图,要得到AB∥CD,下列结论正确的是(??? )
A.?∠A=∠EBC????????????????????B.?∠ABC=∠DCF????????????????????C.?∠B=∠D????????????????????D.?∠A+∠ABC=180°
3. 如图,EF∥BC,AC平分∠BAF,∠B=50°,则∠C的度数是( )
?
A.?50°???????????????????????????????????????B.?55°???????????????????????????????????????C.?60°???????????????????????????????????????D.?65°
4. 如图,若AB∥DC,那么(?? )
A.?∠1=∠2????????????????????????B.?∠3=∠4????????????????????????C.?∠B=∠D????????????????????????D.?∠B=∠3
5. 如图,直线c、b被直线a所截,则∠1与∠2是(????? )
A.?同位角???????????????????????????????B.?内错角???????????????????????????????C.?同旁内角???????????????????????????????D.?对顶角
6. 图中,与∠1成同位角的个数是( )
A.?2个??????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
7. 下图中,∠1和∠2是同位角的是 ( )
A.?②③??????????????????????????????????B.?①②③??????????????????????????????????C.?①②④??????????????????????????????????D.?①④
8. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,下列结论:
①AD是∠BAC的平分线;②∠ADB=120°;③AD=BD;④DB=2CD。
其中正确的结论共有( )
?
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
二、填空题(共4题;共24分)
1. 如图所示,一条公路两次转弯后,和原来的方向相同,如果第一次拐的角是36°,第二次拐的角是________度,根据________________。
2. 如图,写出一个能使a∥b的条件:________________。
3. 如图所示,想在河堤两岸塔建一座桥,搭建方式最短的是________________,理由_________________。
4. 填空并完成推理过程. 如图,E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
解:∵∠1=∠2,(已知)
∠1=∠3(________)
∴∠2=∠3,(等量代换)
∴________∥________,(________)
∴∠C=∠ABD,(________)
又∵∠C=∠D,(已知)
∴∠D=∠ABD,(________)
∴AC∥DF.(________)
三、解答题(共2题;共10分)
1. 如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数。
2. 如图,一个“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由。
四、综合题(共3题;共34分)
1. 两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角。
(1)画出示意图,标出∠1,∠2,∠3。
(2)若∠1=2∠2,∠2=2∠3,求∠3的度数。
2. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F。
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=110°,求∠ACB的度数。
3. 阅读解题过程,回答问题. 如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数。
解:过O点作射线OM,使点M,O,A在同一直线上。
因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,
所以∠BOC=∠MOD,
所以∠AOD=180°﹣∠BOC=180°﹣30°=150°
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数。
答案
一、1. B 2. B 3. D 4.B 5. A 6. B 7. C 8.A
二、
1. 36;两直线平行,内错角相等
2. ∠4=∠5或∠1=∠2或∠3+∠5=180°
3. PN;垂线段最短
4. 对顶角相等;DB;EC;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行
三、
1.解:∵∠2=65°
∴∠1=∠2=65°(对顶角相等)
又∠1=2∠3
∴∠3= ∠1=32.5°
∴∠4=∠3=32.5°(对顶角相等)
2.解:OA∥BC,OB∥AC.理由如下:
因为∠1=50°,∠2=50°,
所以∠1=∠2.
所以OB∥AC.
因为∠2=50°,∠3=130°,
所以∠2+∠3=180°.
所以OA∥BC.
四、1. (1)解:如图所示:
(2)解:∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
故x+4x=180°,
解得:x=36°,
故∠3的度数为36°.
2. (1)解:CD∥EF,
理由:∵ CD⊥AB,EF⊥AB?,
∴CD∥EF;
(2)解:∵CD∥EF,∴∠BCD=∠2,
∵∠1=∠2?,∴∠BCD=∠1,
∴DG∥BC,
∴∠ACB=∠3=110°.
3.(1)解:如果∠BOC=60°,那么∠AOD=180°﹣60°=120° 如果∠BOC=n°,那么∠AOD=180°﹣n°
(2)解:因为∠AOB=∠DOC=x°,∠AOD=y°, 且∠AOD=∠AOB+∠DOC﹣∠BOC
所以∠BOC=∠AOB+∠DOC﹣∠AOD
=2x°﹣y°
姓名: 班级: 座号:
一、单选题(共8题;共32分)
1. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度是(? ?? )
A.?第一次右拐50°,第二次左拐130°??????????????????????????B.?第一次左拐50°,第二次右拐50°
C.?第一次左拐50°,第二次左拐130°???????????????????????D.?第一次右拐50°,第二次右拐50°
2. 如图,要得到AB∥CD,下列结论正确的是(??? )
A.?∠A=∠EBC????????????????????B.?∠ABC=∠DCF????????????????????C.?∠B=∠D????????????????????D.?∠A+∠ABC=180°
3. 如图,EF∥BC,AC平分∠BAF,∠B=50°,则∠C的度数是( )
?
A.?50°???????????????????????????????????????B.?55°???????????????????????????????????????C.?60°???????????????????????????????????????D.?65°
4. 如图,若AB∥DC,那么(?? )
A.?∠1=∠2????????????????????????B.?∠3=∠4????????????????????????C.?∠B=∠D????????????????????????D.?∠B=∠3
5. 如图,直线c、b被直线a所截,则∠1与∠2是(????? )
A.?同位角???????????????????????????????B.?内错角???????????????????????????????C.?同旁内角???????????????????????????????D.?对顶角
6. 图中,与∠1成同位角的个数是( )
A.?2个??????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
7. 下图中,∠1和∠2是同位角的是 ( )
A.?②③??????????????????????????????????B.?①②③??????????????????????????????????C.?①②④??????????????????????????????????D.?①④
8. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,下列结论:
①AD是∠BAC的平分线;②∠ADB=120°;③AD=BD;④DB=2CD。
其中正确的结论共有( )
?
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
二、填空题(共4题;共24分)
1. 如图所示,一条公路两次转弯后,和原来的方向相同,如果第一次拐的角是36°,第二次拐的角是________度,根据________________。
2. 如图,写出一个能使a∥b的条件:________________。
3. 如图所示,想在河堤两岸塔建一座桥,搭建方式最短的是________________,理由_________________。
4. 填空并完成推理过程. 如图,E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
解:∵∠1=∠2,(已知)
∠1=∠3(________)
∴∠2=∠3,(等量代换)
∴________∥________,(________)
∴∠C=∠ABD,(________)
又∵∠C=∠D,(已知)
∴∠D=∠ABD,(________)
∴AC∥DF.(________)
三、解答题(共2题;共10分)
1. 如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数。
2. 如图,一个“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由。
四、综合题(共3题;共34分)
1. 两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角。
(1)画出示意图,标出∠1,∠2,∠3。
(2)若∠1=2∠2,∠2=2∠3,求∠3的度数。
2. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F。
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=110°,求∠ACB的度数。
3. 阅读解题过程,回答问题. 如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数。
解:过O点作射线OM,使点M,O,A在同一直线上。
因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,
所以∠BOC=∠MOD,
所以∠AOD=180°﹣∠BOC=180°﹣30°=150°
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数。
答案
一、1. B 2. B 3. D 4.B 5. A 6. B 7. C 8.A
二、
1. 36;两直线平行,内错角相等
2. ∠4=∠5或∠1=∠2或∠3+∠5=180°
3. PN;垂线段最短
4. 对顶角相等;DB;EC;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行
三、
1.解:∵∠2=65°
∴∠1=∠2=65°(对顶角相等)
又∠1=2∠3
∴∠3= ∠1=32.5°
∴∠4=∠3=32.5°(对顶角相等)
2.解:OA∥BC,OB∥AC.理由如下:
因为∠1=50°,∠2=50°,
所以∠1=∠2.
所以OB∥AC.
因为∠2=50°,∠3=130°,
所以∠2+∠3=180°.
所以OA∥BC.
四、1. (1)解:如图所示:
(2)解:∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
故x+4x=180°,
解得:x=36°,
故∠3的度数为36°.
2. (1)解:CD∥EF,
理由:∵ CD⊥AB,EF⊥AB?,
∴CD∥EF;
(2)解:∵CD∥EF,∴∠BCD=∠2,
∵∠1=∠2?,∴∠BCD=∠1,
∴DG∥BC,
∴∠ACB=∠3=110°.
3.(1)解:如果∠BOC=60°,那么∠AOD=180°﹣60°=120° 如果∠BOC=n°,那么∠AOD=180°﹣n°
(2)解:因为∠AOB=∠DOC=x°,∠AOD=y°, 且∠AOD=∠AOB+∠DOC﹣∠BOC
所以∠BOC=∠AOB+∠DOC﹣∠AOD
=2x°﹣y°
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
