北师大版七年级数学下册同步测试4.3探索三角形全等的条件(含答案)
文档属性
| 名称 | 北师大版七年级数学下册同步测试4.3探索三角形全等的条件(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 110.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-15 00:00:00 | ||
图片预览


文档简介
北师大版七年级数学下册同步测试-4.3《探索三角形全等的条件》
姓名: 班级: 座号:
一、单选题(共8题;共32分)
1. 如图,已知 ,添加条件后,可得 ,则在下列条件中,不能添加的是(???? )。
A.????????????????????B.????????????????????C.????????????????????D.?
2. 如图,AB=AC,BD=CD,则△ABD≌△ACD的依据是(?? )。
A.?SSS??????????????????????????????????????B.?SAS??????????????????????????????????????C.?AAS??????????????????????????????????????D.?HL
3. 全等三角形是(??? )。
A.?三个角对应相等的三角形????????????????????????????????????B.?周长相等的两个三角形
C.?面积相等的两个三角形???????????????????????????????????????D.?三边对应相等的两个三角形
4. 图中两个三角形的关系是(?? ?)。
A.?它们的面积相等??????????????????????B.?它们的周长相等??????????????????????C.?它们全等??????????????????????D.?不确定
5. 如图,已知AC与BD相交于点O,OA=OC,OB=OD,则图中有多少对三角形全等(?? )。
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
6. 如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是(?? )。
A.?AD=AE??????????????????????????????B.?AB=AC??????????????????????????????C.?BD=AE??????????????????????????????D.?AD=CE
7. 如图所示,AB∥EF∥CD , ∠ABC=90°,AB=DC , 那么图中的全等三角形有(? ? )。
A.?1对???????????????????????????????????????B.?2对???????????????????????????????????????C.?3对???????????????????????????????????????D.?4对
8. 如图: ,要使 ,则只要(???? ? )。
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
二、填空题(共6题;共32分)
1. 如图所示,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件________,使△ABC≌△DBE(只需添加一个即可,不添加辅助线).
2. 如图,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样做的数学道理是________.
3. 用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是________?(写出全等的简写)
4. 如图,已知∠3=∠4,要说明△ABC≌△DCB,
(1)若以“SAS”为依据,则需添加一个条件是________?
(2)若以“AAS”为依据,则需添加一个条件是________?
(3)若以“ASA”为依据,则需添加一个条件是________?
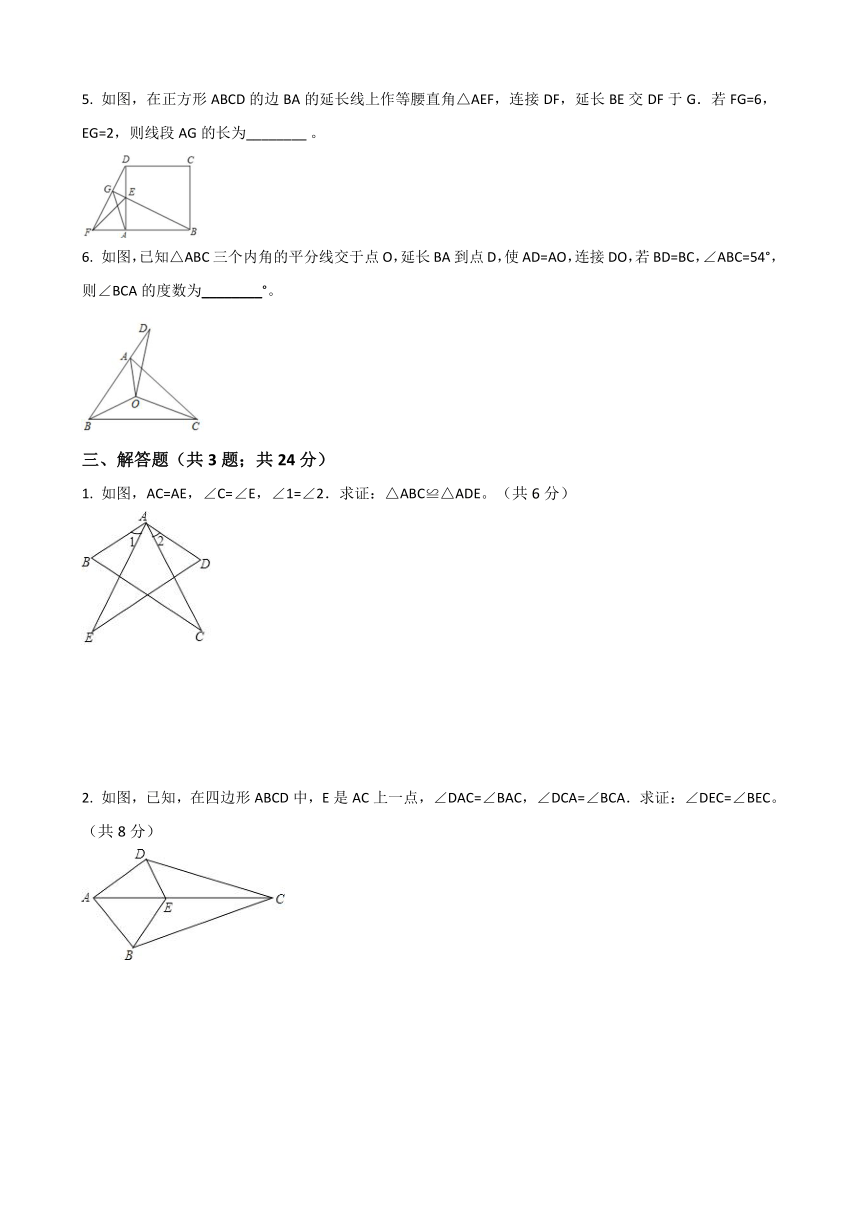
5. 如图,在正方形ABCD的边BA的延长线上作等腰直角△AEF,连接DF,延长BE交DF于G.若FG=6,EG=2,则线段AG的长为________?。
6. 如图,已知△ABC三个内角的平分线交于点O,延长BA到点D,使AD=AO,连接DO,若BD=BC,∠ABC=54°,则∠BCA的度数为________°。
三、解答题(共3题;共24分)
1. 如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE。(共6分)
2. 如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC=∠BEC。(共8分)
3. 如图,在△ABC中,AD⊥BC,BE⊥AC,AD=BD,求证:BF=AC。(共10分)
四、综合题(共12分)
如图,已知,BD与CE相交于点O,AD=AE,∠B=∠C,请解答下列问题:
(1)△ABD与△ACE全等吗?为什么?
(2)BO与CO相等吗?为什么?
答案
一、1. D 2.A 3. D 4. C 5. D 6. A 7. C 8. A
二、
1. ∠BDE=∠BAC或BE=BC或∠ACB=∠DEB.(写出一个即可).
2. 三角形的稳定性
3. SSS
4. AC=DB;∠5=∠6;∠1=∠2
5. 4
6. 42
三、
1.证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,
∴∠BAC=∠DAE,
在△ABC和△ADE中
∴△ABC≌△ADE(SAS)
2.证明:在△ACD和△ACB中,
∴△ACD≌△ACB,(ASA)
∴BC=CD,
在△DCE和△BCE中,
∴△DCE≌△BCE(ASA),
∴∠DEC=∠BEC.
3.证明:∵AD⊥BC,BE⊥AC,∴∠BDF=∠ADC=∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
在△BDF和△ADC中,
∴△BDF≌△ADC(ASA),
∴BF=AC
四、
(1)解:△ABD与△ACE全等,理由:
在△ABD与△ACE中
∵∠A=∠A,∠B=∠C,AD=AE,
∴△ABD≌△ACE(AAS)
(2)解:BO与CO相等,理由:
∵△ABD≌△ACE,
∴AB=AC,
∵AE=AD,
∴AB﹣AE=AC﹣AD,
即BE=CD,
在△BOE与△COD中,
∵∠EOB=∠DOC,∠B=∠C,BE=CD,
∴△BOE≌△COD(AAS).
∴BO=CO
姓名: 班级: 座号:
一、单选题(共8题;共32分)
1. 如图,已知 ,添加条件后,可得 ,则在下列条件中,不能添加的是(???? )。
A.????????????????????B.????????????????????C.????????????????????D.?
2. 如图,AB=AC,BD=CD,则△ABD≌△ACD的依据是(?? )。
A.?SSS??????????????????????????????????????B.?SAS??????????????????????????????????????C.?AAS??????????????????????????????????????D.?HL
3. 全等三角形是(??? )。
A.?三个角对应相等的三角形????????????????????????????????????B.?周长相等的两个三角形
C.?面积相等的两个三角形???????????????????????????????????????D.?三边对应相等的两个三角形
4. 图中两个三角形的关系是(?? ?)。
A.?它们的面积相等??????????????????????B.?它们的周长相等??????????????????????C.?它们全等??????????????????????D.?不确定
5. 如图,已知AC与BD相交于点O,OA=OC,OB=OD,则图中有多少对三角形全等(?? )。
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
6. 如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是(?? )。
A.?AD=AE??????????????????????????????B.?AB=AC??????????????????????????????C.?BD=AE??????????????????????????????D.?AD=CE
7. 如图所示,AB∥EF∥CD , ∠ABC=90°,AB=DC , 那么图中的全等三角形有(? ? )。
A.?1对???????????????????????????????????????B.?2对???????????????????????????????????????C.?3对???????????????????????????????????????D.?4对
8. 如图: ,要使 ,则只要(???? ? )。
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
二、填空题(共6题;共32分)
1. 如图所示,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件________,使△ABC≌△DBE(只需添加一个即可,不添加辅助线).
2. 如图,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样做的数学道理是________.
3. 用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是________?(写出全等的简写)
4. 如图,已知∠3=∠4,要说明△ABC≌△DCB,
(1)若以“SAS”为依据,则需添加一个条件是________?
(2)若以“AAS”为依据,则需添加一个条件是________?
(3)若以“ASA”为依据,则需添加一个条件是________?
5. 如图,在正方形ABCD的边BA的延长线上作等腰直角△AEF,连接DF,延长BE交DF于G.若FG=6,EG=2,则线段AG的长为________?。
6. 如图,已知△ABC三个内角的平分线交于点O,延长BA到点D,使AD=AO,连接DO,若BD=BC,∠ABC=54°,则∠BCA的度数为________°。
三、解答题(共3题;共24分)
1. 如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE。(共6分)
2. 如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC=∠BEC。(共8分)
3. 如图,在△ABC中,AD⊥BC,BE⊥AC,AD=BD,求证:BF=AC。(共10分)
四、综合题(共12分)
如图,已知,BD与CE相交于点O,AD=AE,∠B=∠C,请解答下列问题:
(1)△ABD与△ACE全等吗?为什么?
(2)BO与CO相等吗?为什么?
答案
一、1. D 2.A 3. D 4. C 5. D 6. A 7. C 8. A
二、
1. ∠BDE=∠BAC或BE=BC或∠ACB=∠DEB.(写出一个即可).
2. 三角形的稳定性
3. SSS
4. AC=DB;∠5=∠6;∠1=∠2
5. 4
6. 42
三、
1.证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,
∴∠BAC=∠DAE,
在△ABC和△ADE中
∴△ABC≌△ADE(SAS)
2.证明:在△ACD和△ACB中,
∴△ACD≌△ACB,(ASA)
∴BC=CD,
在△DCE和△BCE中,
∴△DCE≌△BCE(ASA),
∴∠DEC=∠BEC.
3.证明:∵AD⊥BC,BE⊥AC,∴∠BDF=∠ADC=∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
在△BDF和△ADC中,
∴△BDF≌△ADC(ASA),
∴BF=AC
四、
(1)解:△ABD与△ACE全等,理由:
在△ABD与△ACE中
∵∠A=∠A,∠B=∠C,AD=AE,
∴△ABD≌△ACE(AAS)
(2)解:BO与CO相等,理由:
∵△ABD≌△ACE,
∴AB=AC,
∵AE=AD,
∴AB﹣AE=AC﹣AD,
即BE=CD,
在△BOE与△COD中,
∵∠EOB=∠DOC,∠B=∠C,BE=CD,
∴△BOE≌△COD(AAS).
∴BO=CO
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
