北师大版七年级数学下册同步测试4.5利用三角形全等测距离(含答案)
文档属性
| 名称 | 北师大版七年级数学下册同步测试4.5利用三角形全等测距离(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 201.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-15 14:45:27 | ||
图片预览


文档简介
北师大版七年级数学下册4.5《利用三角形全等测距离》同步测试
姓名: 班级: 座号:
一、单选题(共8题;共32分)
1. 如图,某同学把一块三角形的玻璃打破成了三块,现在他要到玻璃店去配一块完全一样形状的玻璃,那么最省事的办法是带( )去配。
A.?①???????????????????????????????????????B.?②???????????????????????????????????????C.?③???????????????????????????????????????D.?①和②
2. 如图,两棵大树间相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为lm/s,小华走的时间是(? ? )。
A.?13???????????????????????????????????????????B.?8???????????????????????????????????????????C.?6???????????????????????????????????????????D.?5
3. 如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是(? ? ) 。
A.?AAS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?SSS
4. 小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是(?? ) 。
A.?∠BOA=∠DOC???????????????B.?AB∥CD???????????????C.?∠ABD=90°???????????????D.?与∠AOE相等的角共有2个
5. 要测量河岸相对两点A、B的距离,已知AB垂直于河岸BF,先在BF上取两点C、D,使CD=CB,再过点D作BF的垂线段DE,使点A、C、E在一条直线上,如图,测出BD=10,ED=5,则AB的长是(?? ) 。
A.?2.5?????????????????????????????????????B.?10?????????????????????????????????????C.?5?????????????????????????????????????D.?以上都不对
6. 下列选项中,不是依据三角形全等知识解决问题的是( )。
A.?利用尺规作图,作一个角等于已知角??????????????????B.?工人师傅用角尺平分任意角
C.?利用卡钳测量内槽的宽???????????????????????????????????????D.?用放大镜观察蚂蚁的触角
7. 如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )。
A.?△ABD和△CDB的面积相等???????????????????????????????????B.?△ABD和△CDB的周长相等
C.?∠A+∠ABD=∠C+∠CBD?????????????????????????????????????D.?AD∥BC,且AD=BC
8. 如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图所示),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是(?? ) 。
A.?边角边????????????????????????????????B.?角边角????????????????????????????????C.?边边边????????????????????????????????D.?边边角
二、填空题(共7题;共36分)
1. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带_____________依据______________。
2.把两根钢条AA′、BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),如图,若测得AB=5厘米,则槽宽为________米.
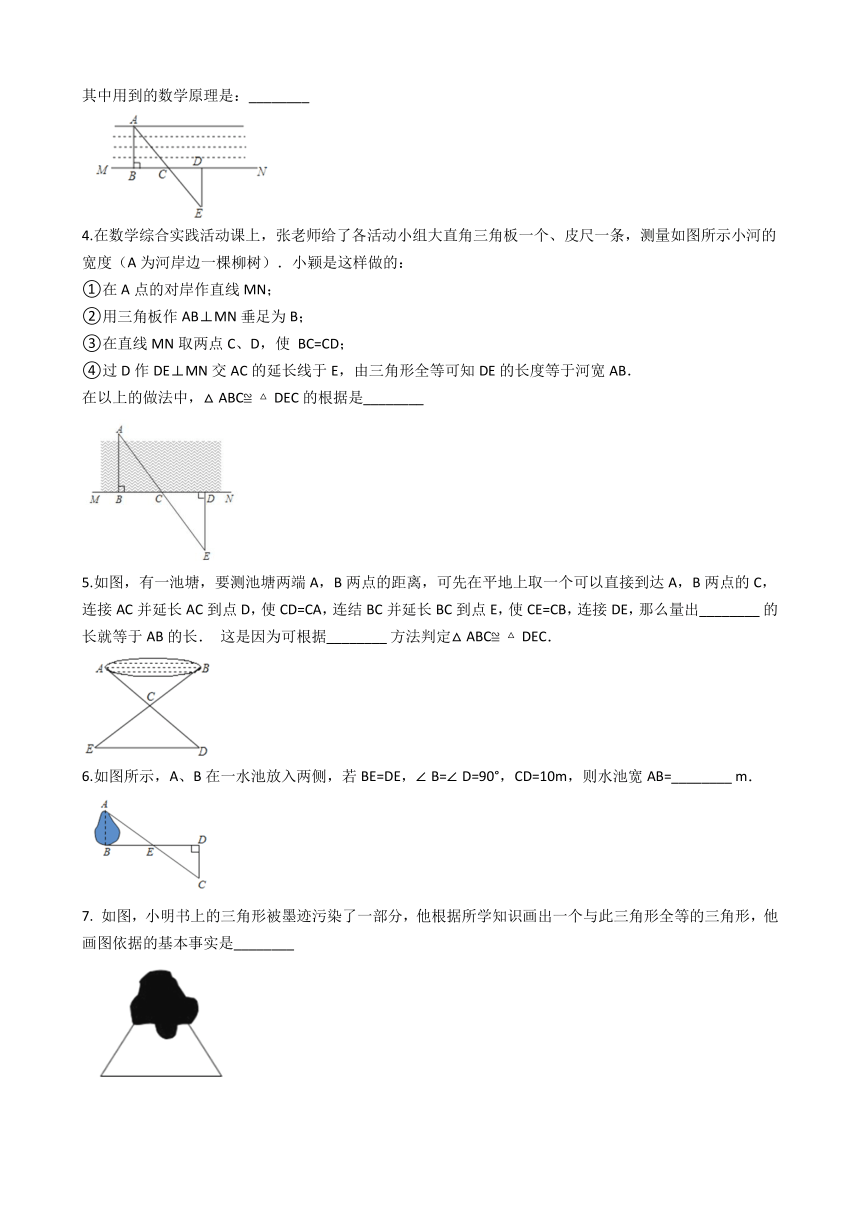
3. 如图,要测量一条小河的宽度AB的长,可以在小河的岸边作AB的垂线 MN,然后在MN上取两点C,D,使BC=CD,再画出MN的垂线DE,并使点E 与点A,C在一条直线上,这时测得DE的长就是AB的长,其中用到的数学原理是:________?
4.在数学综合实践活动课上,张老师给了各活动小组大直角三角板一个、皮尺一条,测量如图所示小河的宽度(A为河岸边一棵柳树).小颖是这样做的:
①在A点的对岸作直线MN;
②用三角板作AB⊥MN垂足为B;
③在直线MN取两点C、D,使 BC=CD;
④过D作DE⊥MN交AC的延长线于E,由三角形全等可知DE的长度等于河宽AB.
在以上的做法中,△ABC≌△DEC的根据是________?
5.如图,有一池塘,要测池塘两端A,B两点的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连结BC并延长BC到点E,使CE=CB,连接DE,那么量出________?的长就等于AB的长. 这是因为可根据________?方法判定△ABC≌△DEC.
6.如图所示,A、B在一水池放入两侧,若BE=DE,∠B=∠D=90°,CD=10m,则水池宽AB=________?m.
7. 如图,小明书上的三角形被墨迹污染了一部分,他根据所学知识画出一个与此三角形全等的三角形,他画图依据的基本事实是________?
三、解答题(共4题;共20分)
1.课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图,求证:△ADC≌△CEB。
2.如图:A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长.他叔叔帮他出了一个这样的主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到E,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出DE=8m;
问题:DE=AB吗?AB的长度是多少?请说明理由。
3.小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
4. 如图,AD是一段斜坡,AB是水平线,现为了测斜坡上一点D的铅直高度(即垂线段DB的长度),小亮在D处立上一竹竿CD,并保证CD=AB,CD⊥AD,然后在竿顶C处垂下一根细绳.(细绳末端挂一重锤,以使细绳与水平线垂直).细绳与斜坡AD交于点E,此时他测得DE=2米,求DB的长度。
四、综合题(共12分)
如图,点B,F,C,E在直线l上(点F,点C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
答案
一、1. A 2. B 3. B 4. D 5.C 6. D 7. C 8. B
二、
1. 2;角边角
2. 0.05
3. ASA,全等三角形对应边相等
4. ASA
5. DE;SAS
6. 10
7. 两角及其夹边分别相等的两个三角形全等
三、
1. 证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
∵,
∴△ADC≌△CEB(AAS).
2.解:由题意知AC=DC,BC=EC,且∠ACB=∠DCE,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(SAS),
∴DE=AB.
故量出DE的长,就是A,B两点间的距离
3.解:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°,
在△CPD和△PAB中
∵,
∴△CPD≌△PAB(ASA),
∴DP=AB,
∵DB=36,PB=10,
∴AB=36﹣10=26(m),
答:楼高AB是26米.
4.解:如图,延长CE交AB于F,
则∠A+∠1=90°,∠C+∠2=90°,
∵∠1=∠2(对顶角相等),
∴∠A=∠C,
在△ABD和△CDE中,
,
∴△ABD≌△CDE(AAS),
∴DB=DE,
∵DE=2米,
∴DB的长度是2米.
四、
(1)证明:∵BF=CE, ∴BF+FC=FC+CE,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS)
(2)解:结论:AB∥DE,AC∥DF. 理由:∵△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE,
∴AB∥DE,AC∥DF
姓名: 班级: 座号:
一、单选题(共8题;共32分)
1. 如图,某同学把一块三角形的玻璃打破成了三块,现在他要到玻璃店去配一块完全一样形状的玻璃,那么最省事的办法是带( )去配。
A.?①???????????????????????????????????????B.?②???????????????????????????????????????C.?③???????????????????????????????????????D.?①和②
2. 如图,两棵大树间相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为lm/s,小华走的时间是(? ? )。
A.?13???????????????????????????????????????????B.?8???????????????????????????????????????????C.?6???????????????????????????????????????????D.?5
3. 如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是(? ? ) 。
A.?AAS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?SSS
4. 小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是(?? ) 。
A.?∠BOA=∠DOC???????????????B.?AB∥CD???????????????C.?∠ABD=90°???????????????D.?与∠AOE相等的角共有2个
5. 要测量河岸相对两点A、B的距离,已知AB垂直于河岸BF,先在BF上取两点C、D,使CD=CB,再过点D作BF的垂线段DE,使点A、C、E在一条直线上,如图,测出BD=10,ED=5,则AB的长是(?? ) 。
A.?2.5?????????????????????????????????????B.?10?????????????????????????????????????C.?5?????????????????????????????????????D.?以上都不对
6. 下列选项中,不是依据三角形全等知识解决问题的是( )。
A.?利用尺规作图,作一个角等于已知角??????????????????B.?工人师傅用角尺平分任意角
C.?利用卡钳测量内槽的宽???????????????????????????????????????D.?用放大镜观察蚂蚁的触角
7. 如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )。
A.?△ABD和△CDB的面积相等???????????????????????????????????B.?△ABD和△CDB的周长相等
C.?∠A+∠ABD=∠C+∠CBD?????????????????????????????????????D.?AD∥BC,且AD=BC
8. 如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图所示),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是(?? ) 。
A.?边角边????????????????????????????????B.?角边角????????????????????????????????C.?边边边????????????????????????????????D.?边边角
二、填空题(共7题;共36分)
1. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带_____________依据______________。
2.把两根钢条AA′、BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),如图,若测得AB=5厘米,则槽宽为________米.
3. 如图,要测量一条小河的宽度AB的长,可以在小河的岸边作AB的垂线 MN,然后在MN上取两点C,D,使BC=CD,再画出MN的垂线DE,并使点E 与点A,C在一条直线上,这时测得DE的长就是AB的长,其中用到的数学原理是:________?
4.在数学综合实践活动课上,张老师给了各活动小组大直角三角板一个、皮尺一条,测量如图所示小河的宽度(A为河岸边一棵柳树).小颖是这样做的:
①在A点的对岸作直线MN;
②用三角板作AB⊥MN垂足为B;
③在直线MN取两点C、D,使 BC=CD;
④过D作DE⊥MN交AC的延长线于E,由三角形全等可知DE的长度等于河宽AB.
在以上的做法中,△ABC≌△DEC的根据是________?
5.如图,有一池塘,要测池塘两端A,B两点的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连结BC并延长BC到点E,使CE=CB,连接DE,那么量出________?的长就等于AB的长. 这是因为可根据________?方法判定△ABC≌△DEC.
6.如图所示,A、B在一水池放入两侧,若BE=DE,∠B=∠D=90°,CD=10m,则水池宽AB=________?m.
7. 如图,小明书上的三角形被墨迹污染了一部分,他根据所学知识画出一个与此三角形全等的三角形,他画图依据的基本事实是________?
三、解答题(共4题;共20分)
1.课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图,求证:△ADC≌△CEB。
2.如图:A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长.他叔叔帮他出了一个这样的主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到E,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出DE=8m;
问题:DE=AB吗?AB的长度是多少?请说明理由。
3.小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
4. 如图,AD是一段斜坡,AB是水平线,现为了测斜坡上一点D的铅直高度(即垂线段DB的长度),小亮在D处立上一竹竿CD,并保证CD=AB,CD⊥AD,然后在竿顶C处垂下一根细绳.(细绳末端挂一重锤,以使细绳与水平线垂直).细绳与斜坡AD交于点E,此时他测得DE=2米,求DB的长度。
四、综合题(共12分)
如图,点B,F,C,E在直线l上(点F,点C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
答案
一、1. A 2. B 3. B 4. D 5.C 6. D 7. C 8. B
二、
1. 2;角边角
2. 0.05
3. ASA,全等三角形对应边相等
4. ASA
5. DE;SAS
6. 10
7. 两角及其夹边分别相等的两个三角形全等
三、
1. 证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
∵,
∴△ADC≌△CEB(AAS).
2.解:由题意知AC=DC,BC=EC,且∠ACB=∠DCE,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(SAS),
∴DE=AB.
故量出DE的长,就是A,B两点间的距离
3.解:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°,
在△CPD和△PAB中
∵,
∴△CPD≌△PAB(ASA),
∴DP=AB,
∵DB=36,PB=10,
∴AB=36﹣10=26(m),
答:楼高AB是26米.
4.解:如图,延长CE交AB于F,
则∠A+∠1=90°,∠C+∠2=90°,
∵∠1=∠2(对顶角相等),
∴∠A=∠C,
在△ABD和△CDE中,
,
∴△ABD≌△CDE(AAS),
∴DB=DE,
∵DE=2米,
∴DB的长度是2米.
四、
(1)证明:∵BF=CE, ∴BF+FC=FC+CE,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS)
(2)解:结论:AB∥DE,AC∥DF. 理由:∵△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE,
∴AB∥DE,AC∥DF
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
