2020鲁教版五四制七上数学2.3简单的轴对称图形第1课时课件(30张PPT)
文档属性
| 名称 | 2020鲁教版五四制七上数学2.3简单的轴对称图形第1课时课件(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-15 00:00:00 | ||
图片预览








文档简介
课件30张PPT。3 简单的轴对称图形
第1课时1.了解线段垂直平分线及角的平分线的性质和判定.
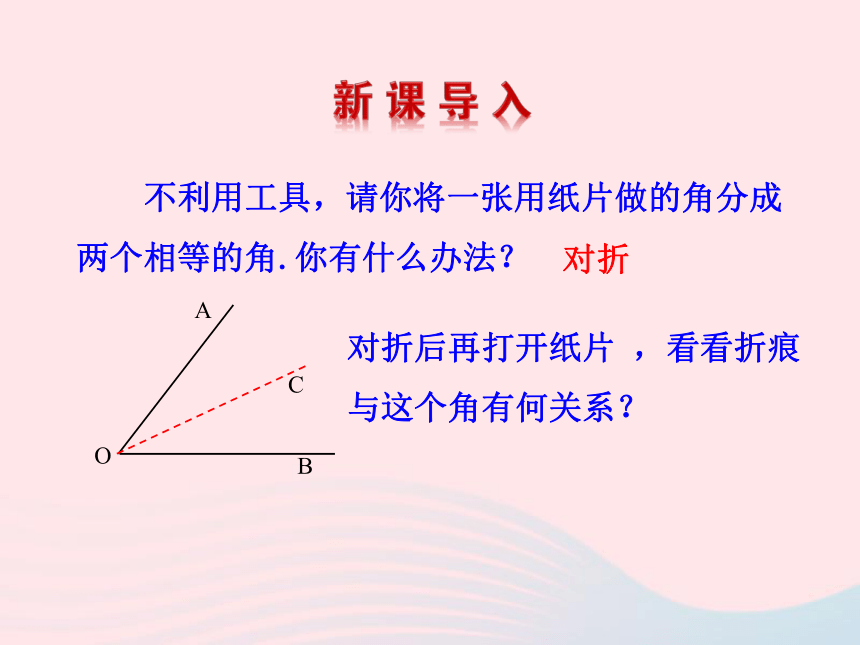
2.会应用线段垂直平分线及角的平分线的性质和判定解决问题. 不利用工具,请你将一张用纸片做的角分成两个相等的角.你有什么办法?对折后再打开纸片 ,看看折痕与这个角有何关系? 对折【探究】画线段AB的垂直平分线l,在l上取任意点P,量一量点P到A与B的距离,你有什么发现?再取几个点试试.你能说明理由吗?结论:线段垂直平分线上的点到这条线段两个端点的距离相等.反过来,若AP=BP,则P在线段AB的垂直平分线上.结论:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.线段的垂直平分线可以看成是到线段两端点距离相等的所有点的集合. 1.如图,MN是线段AB的垂直平分线,下列说法正确的有: .
①AB⊥MN,②AD=DB,③MD=DN,
④ AB是MN的垂直平分线.①②【练一练】2.下列说法:①若直线PE是线段AB的垂直平分线,则
EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分
线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上
的点;④若EA=EB,则过点E的直线垂直平分线段AB.其
中正确的有( )
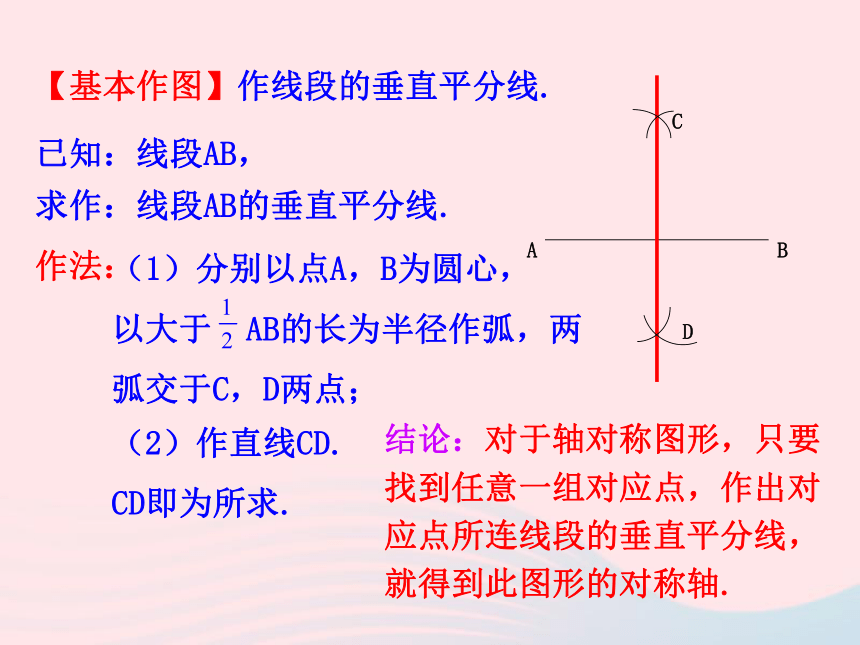
A.1个 B.2个 C.3个 D.4个C 问题思考:既然轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线,那么轴对称图形的对称轴如何来作呢?【思考】如何作出线段的垂直平分线? 由两点确定一条直线和线段垂直平分线的性质可知,只要作出到线段两端点距离相等的两点并连接即可. 【基本作图】作线段的垂直平分线.已知:线段AB,
求作:线段AB的垂直平分线.CD作法:(2)作直线CD.
CD即为所求.结论:对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.(1)分别以点A,B为圆心,
以大于 AB的长为半径作弧,两弧交于C,D两点;1.下图中的五角星有几条对称轴?作出这些对称轴. AB作法:(1)找出五角星的一对
对应点A和B,连接AB.
(2)作出线段AB的垂直平分线n.
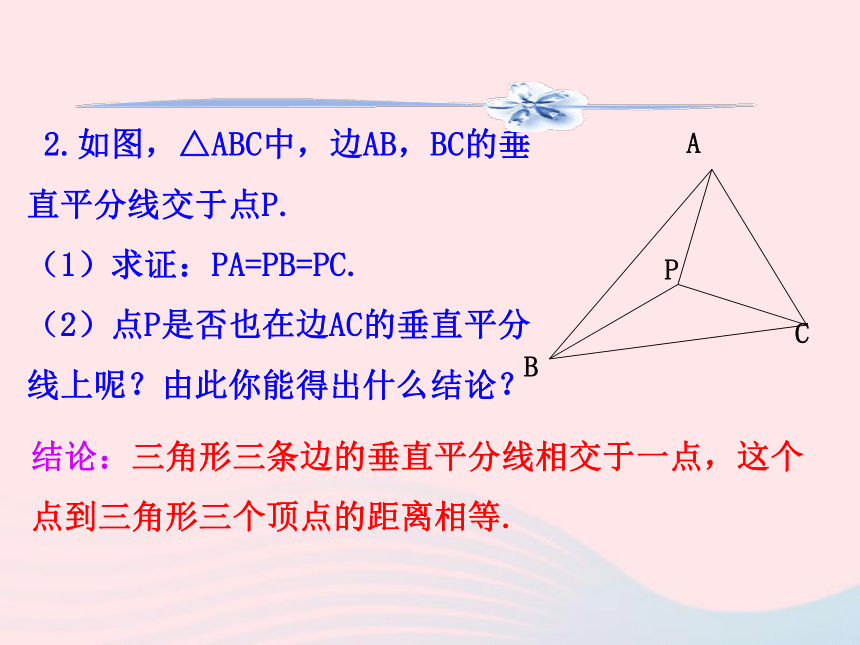
则n就是这个五角星的一条对称轴. n用同样的方法,可以找出五条对称轴,所以五角星有五条对称轴. 【跟踪训练】 2.如图,△ABC中,边AB,BC的垂直平分线交于点P.
(1)求证:PA=PB=PC.
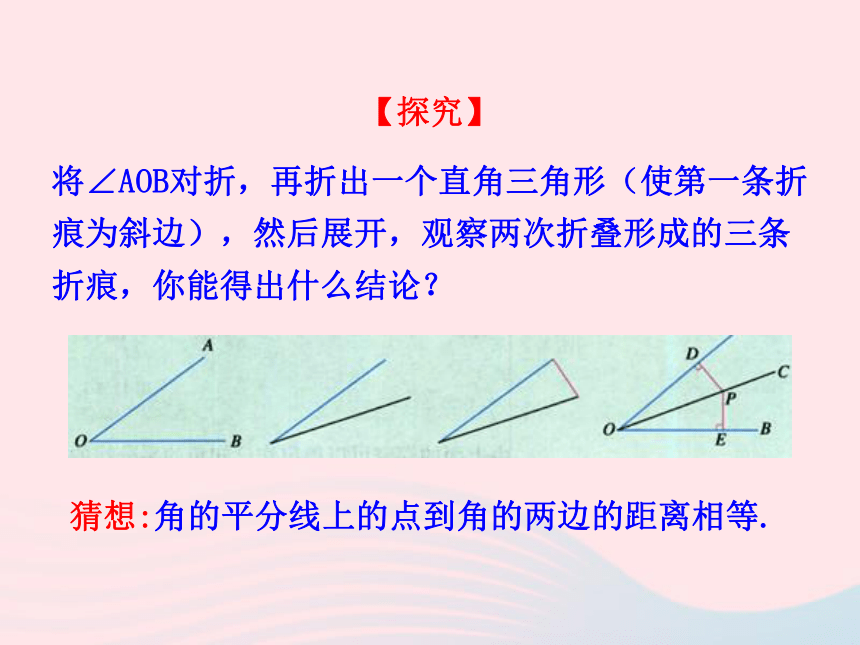
(2)点P是否也在边AC的垂直平分线上呢?由此你能得出什么结论?APCB结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等.猜想:角的平分线上的点到角的两边的距离相等.将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?【探究】【验证】已知:OC平分∠AOB,点P在OC上,PD⊥OA于D,PE⊥OB于E,求证: PD=PE.PED证明:因为 OC平分∠AOB, P是OC上一点(已知)
所以∠DOP=∠BOP(角平分线定义)
因为PD⊥OA,PE⊥OB (已知)
所以∠ODP=∠OEP=90°(垂直的定义)
在△OPD和△OPE中
∠DOP=∠BOP (已证)
∠ODP=∠OEP (已证)
OP=OP (已知)
所以 △OPD≌△OPE(AAS)
所以PD=PE(全等三角形对应边相等)定理:角平分线上的点到这个角的两边的距离相等.用符号语言表示为:因为∠1= ∠2
PD ⊥OA ,PE ⊥OB
所以PD=PE.角的平分线的性质 如图,要在s区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500 m,这个贸易市场应建在何处?(比例尺为1︰20000)【跟踪训练】DCs【解析】 作夹角的角平分线OC,截取OD=2.5cm ,D即为所求.O 反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢? 角的内部到角的两边的距离相等的点在角的平分线上.【结论】(1)因为∠1= ∠2,DC⊥AC, DE⊥AB,
所以________.
(_______________________________________).
(2)因为DC⊥AC ,DE⊥AB ,DC=DE,
所以__________
(_______________________________________________).∠1= ∠2DC=DE角的内部到角的两边的距离相等的点在角的平分线上角的平分线上的点到角的两边的距离相等【跟踪训练】1.(临沂·中考)正方形ABCD边长为a,
点E,F分别是对角线BD上的两点,过点E,
F分别作AD,AB的平行线,如图所示,
则图中阴影部分的面积之和等于 .
【解析】运用轴对称、转化的思想,阴
影部分面积等于正方形面积的一半,为 .
答案:2.直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( ) A.一处 B.两处 C.三处 D.四处【解析】选D.由于没有限制在何处选址,故要求的
地址共有四处,在各自夹角的平分线上,即:A,B,C,D
各一处.3.(宁德·中考)如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:_______________,并给予证明. 【解析】解法一:添加条件:AE=AF.
在△AED与△AFD中,
因为AE=AF,∠EAD=∠FAD,AD=AD,
所以△AED≌△AFD(SAS).
解法二:添加条件:∠EDA=∠FDA.
在△AED与△AFD中,
因为∠EAD=∠FAD,AD=AD,∠EDA=∠FDA,
所以△AED≌△AFD(ASA).
(答案不唯一)4. 有A,B,C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置.ABC【提示】学校在连接任意两点的两条线段的垂直平分线的交点处.5.如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?【提示】连接AB,作AB的垂直平分线,则与公路的交点即是要建的公共汽车站.6.如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长.DCBEA【解析】因为ED是线段AB的垂直平分线,
所以
因为 △BCD的周长=BD+DC+BC,
所以△BCD的周长=
=
=BD=AD,AD+DC+BCAC+BC12+7=19. 7.如图,如果△ACD的周长为18cm,△ABC的周长为28cm, DE是BC的垂直平分线,根据这些条件,你可以求出哪条线段的长? (1)△ACD的周长=AD +CD+AC=18cm;
(2)△ABC的周长=AB+AC+BC=28cm;(3)由DE是BC的垂直平分线得:BD=CD;所以AD+CD
=AD+BD=AB.(4)由(2)-(1)得BC=10cm.【解析】通过本课时的学习,需要我们掌握:3.角的平分线的性质:角的平分线上的点到角的两边的距离相等.4.角平分线的判定:角的内部到角的两边的距离相等的点在角的平分线上.1.线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等.2.线段垂直平分线的判定:到线段两端点的距离相等的点在线段垂直平分线上. 在数学的领域中,提出问题的艺术比解答问题的艺术更为重要.
——康托尔
第1课时1.了解线段垂直平分线及角的平分线的性质和判定.
2.会应用线段垂直平分线及角的平分线的性质和判定解决问题. 不利用工具,请你将一张用纸片做的角分成两个相等的角.你有什么办法?对折后再打开纸片 ,看看折痕与这个角有何关系? 对折【探究】画线段AB的垂直平分线l,在l上取任意点P,量一量点P到A与B的距离,你有什么发现?再取几个点试试.你能说明理由吗?结论:线段垂直平分线上的点到这条线段两个端点的距离相等.反过来,若AP=BP,则P在线段AB的垂直平分线上.结论:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.线段的垂直平分线可以看成是到线段两端点距离相等的所有点的集合. 1.如图,MN是线段AB的垂直平分线,下列说法正确的有: .
①AB⊥MN,②AD=DB,③MD=DN,
④ AB是MN的垂直平分线.①②【练一练】2.下列说法:①若直线PE是线段AB的垂直平分线,则
EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分
线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上
的点;④若EA=EB,则过点E的直线垂直平分线段AB.其
中正确的有( )
A.1个 B.2个 C.3个 D.4个C 问题思考:既然轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线,那么轴对称图形的对称轴如何来作呢?【思考】如何作出线段的垂直平分线? 由两点确定一条直线和线段垂直平分线的性质可知,只要作出到线段两端点距离相等的两点并连接即可. 【基本作图】作线段的垂直平分线.已知:线段AB,
求作:线段AB的垂直平分线.CD作法:(2)作直线CD.
CD即为所求.结论:对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.(1)分别以点A,B为圆心,
以大于 AB的长为半径作弧,两弧交于C,D两点;1.下图中的五角星有几条对称轴?作出这些对称轴. AB作法:(1)找出五角星的一对
对应点A和B,连接AB.
(2)作出线段AB的垂直平分线n.
则n就是这个五角星的一条对称轴. n用同样的方法,可以找出五条对称轴,所以五角星有五条对称轴. 【跟踪训练】 2.如图,△ABC中,边AB,BC的垂直平分线交于点P.
(1)求证:PA=PB=PC.
(2)点P是否也在边AC的垂直平分线上呢?由此你能得出什么结论?APCB结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等.猜想:角的平分线上的点到角的两边的距离相等.将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?【探究】【验证】已知:OC平分∠AOB,点P在OC上,PD⊥OA于D,PE⊥OB于E,求证: PD=PE.PED证明:因为 OC平分∠AOB, P是OC上一点(已知)
所以∠DOP=∠BOP(角平分线定义)
因为PD⊥OA,PE⊥OB (已知)
所以∠ODP=∠OEP=90°(垂直的定义)
在△OPD和△OPE中
∠DOP=∠BOP (已证)
∠ODP=∠OEP (已证)
OP=OP (已知)
所以 △OPD≌△OPE(AAS)
所以PD=PE(全等三角形对应边相等)定理:角平分线上的点到这个角的两边的距离相等.用符号语言表示为:因为∠1= ∠2
PD ⊥OA ,PE ⊥OB
所以PD=PE.角的平分线的性质 如图,要在s区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500 m,这个贸易市场应建在何处?(比例尺为1︰20000)【跟踪训练】DCs【解析】 作夹角的角平分线OC,截取OD=2.5cm ,D即为所求.O 反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢? 角的内部到角的两边的距离相等的点在角的平分线上.【结论】(1)因为∠1= ∠2,DC⊥AC, DE⊥AB,
所以________.
(_______________________________________).
(2)因为DC⊥AC ,DE⊥AB ,DC=DE,
所以__________
(_______________________________________________).∠1= ∠2DC=DE角的内部到角的两边的距离相等的点在角的平分线上角的平分线上的点到角的两边的距离相等【跟踪训练】1.(临沂·中考)正方形ABCD边长为a,
点E,F分别是对角线BD上的两点,过点E,
F分别作AD,AB的平行线,如图所示,
则图中阴影部分的面积之和等于 .
【解析】运用轴对称、转化的思想,阴
影部分面积等于正方形面积的一半,为 .
答案:2.直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( ) A.一处 B.两处 C.三处 D.四处【解析】选D.由于没有限制在何处选址,故要求的
地址共有四处,在各自夹角的平分线上,即:A,B,C,D
各一处.3.(宁德·中考)如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:_______________,并给予证明. 【解析】解法一:添加条件:AE=AF.
在△AED与△AFD中,
因为AE=AF,∠EAD=∠FAD,AD=AD,
所以△AED≌△AFD(SAS).
解法二:添加条件:∠EDA=∠FDA.
在△AED与△AFD中,
因为∠EAD=∠FAD,AD=AD,∠EDA=∠FDA,
所以△AED≌△AFD(ASA).
(答案不唯一)4. 有A,B,C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置.ABC【提示】学校在连接任意两点的两条线段的垂直平分线的交点处.5.如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?【提示】连接AB,作AB的垂直平分线,则与公路的交点即是要建的公共汽车站.6.如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长.DCBEA【解析】因为ED是线段AB的垂直平分线,
所以
因为 △BCD的周长=BD+DC+BC,
所以△BCD的周长=
=
=BD=AD,AD+DC+BCAC+BC12+7=19. 7.如图,如果△ACD的周长为18cm,△ABC的周长为28cm, DE是BC的垂直平分线,根据这些条件,你可以求出哪条线段的长? (1)△ACD的周长=AD +CD+AC=18cm;
(2)△ABC的周长=AB+AC+BC=28cm;(3)由DE是BC的垂直平分线得:BD=CD;所以AD+CD
=AD+BD=AB.(4)由(2)-(1)得BC=10cm.【解析】通过本课时的学习,需要我们掌握:3.角的平分线的性质:角的平分线上的点到角的两边的距离相等.4.角平分线的判定:角的内部到角的两边的距离相等的点在角的平分线上.1.线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等.2.线段垂直平分线的判定:到线段两端点的距离相等的点在线段垂直平分线上. 在数学的领域中,提出问题的艺术比解答问题的艺术更为重要.
——康托尔
