五年级下册数学一课一练-3.2长方体、正方体的表面积 西师大版 (含答案)
文档属性
| 名称 | 五年级下册数学一课一练-3.2长方体、正方体的表面积 西师大版 (含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 72.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-15 14:07:07 | ||
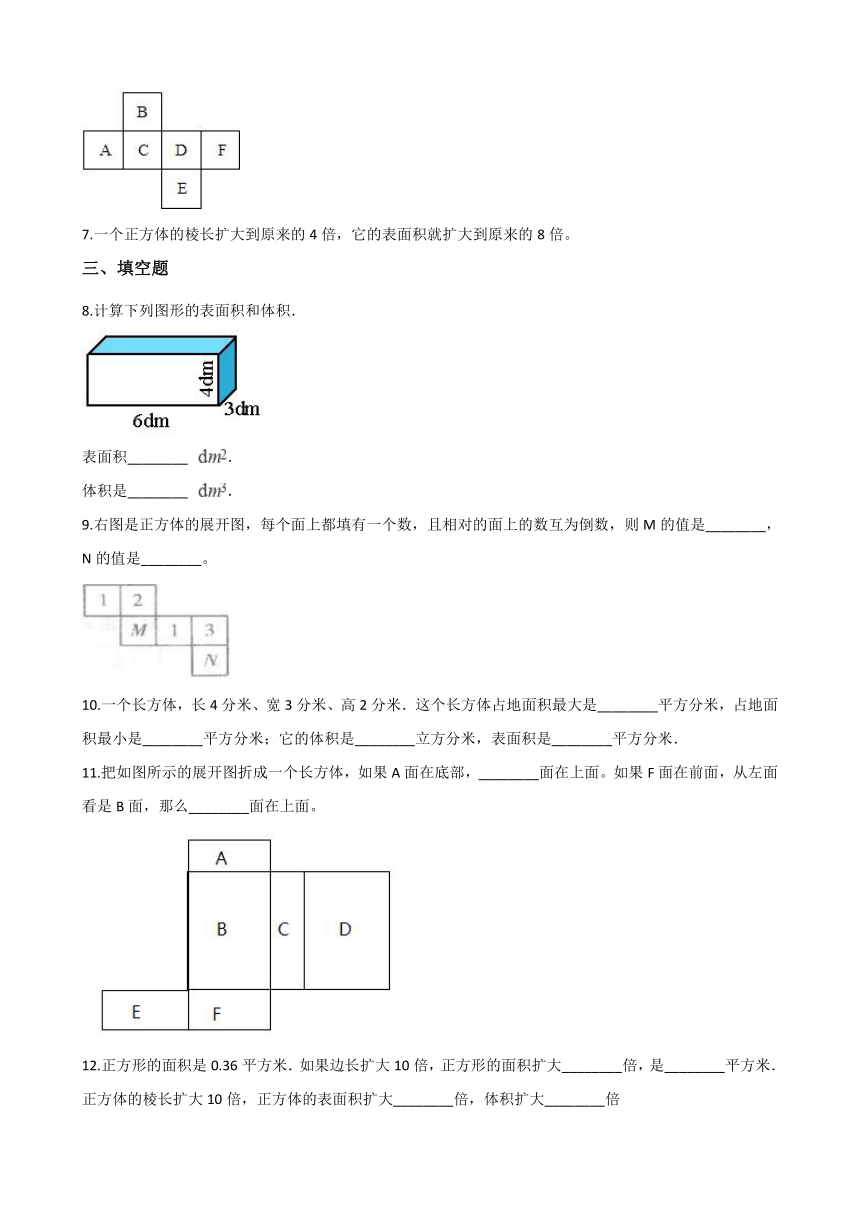
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级下册数学一课一练-3.2长方体、正方体的表面积
一、单选题
1.一个长方体水池,长20米,宽10米,深2米,占地(??? )平方米。
A.?400???????????????????????????????????????B.?200???????????????????????????????????????C.?520???????????????????????????????????????D.?40
2.将一块正方体橡皮泥捏成长方体,正方体和长方体( ??)。
A.?体积相等,表面积不一定相等??????????B.?体积和表面积都不相等??????????C.?表面积相等,体积不相等
3.在一个大正方形上挖去一个棱长是1cm的小正方体,大正方体的表面积发生怎样的变化?
(1)表面积不变的是( ??)
A.??????????????????????????????B.??????????????????????????????C.?
(2)表面积增加2 的是( ??)
A.????????????????????????????????B.????????????????????????????????C.?
(3)表面积增加4 的是(? )
A.?????????????????????????B.?????????????????????????C.?
4.下列图形沿虚线折叠后能围成长方体的有(??? )。
A.?①和②???????????????????????????????B.?①和③???????????????????????????????C.?①③④???????????????????????????????D.?①②③④
二、判断题
5.棱长是6分米的正方体,它的表面积和体积相等。( ??)
6.如图围成正方体后,A面面对的是D面.
7.一个正方体的棱长扩大到原来的4倍,它的表面积就扩大到原来的8倍。
三、填空题
8.计算下列图形的表面积和体积.
表面积________? .
体积是________? .
9.右图是正方体的展开图,每个面上都填有一个数,且相对的面上的数互为倒数,则M的值是________,N的值是________。
10.一个长方体,长4分米、宽3分米、高2分米.这个长方体占地面积最大是________平方分米,占地面积最小是________平方分米;它的体积是________立方分米,表面积是________平方分米.
11.把如图所示的展开图折成一个长方体,如果A面在底部,________面在上面。如果F面在前面,从左面看是B面,那么________面在上面。
12.正方形的面积是0.36平方米.如果边长扩大10倍,正方形的面积扩大________倍,是________平方米.
正方体的棱长扩大10倍,正方体的表面积扩大________倍,体积扩大________倍
四、解答题
13.一个无盖的长方体铁盒,长是2分米,宽是1.5分米,高是1 .8分米,做20个这样的铁盒需要铁皮多少平方米?
14.黄师傅要制作一个无盖玻璃鱼缸。现在有一块长方形钢化玻璃(如下图)用作鱼缸的一个面,需要再补另外4块玻璃。
(1)要做一个底面是正方形的长方体无盖鱼缸,需要补另外4块什么尺寸的玻璃?
(2)制作第(1)题中的长方体无盖鱼缸,一共需要多少平方分米的玻璃?
(3)请你再设计两种不同的长方体鱼缸,要求鱼缸容积大于48L,小于240L。画出草图,并标出长方体鱼缸的长、宽、高。
五、综合题
15.某游泳馆有一个长60米,宽20米,深4米的游泳池。
(1)游泳池的蓄水高度为池深的 ,这个游泳池蓄水多少立方米?
(2)游泳池的底部和四壁都贴有瓷砖,贴瓷砖的面积是多少平方米?
六、应用题
16.底面是正方形的长方体包装盒高20cm,侧面展开后是一个正方形,这个长方体的体积是多少立方厘米?
参考答案
一、单选题
1.【答案】 B
【解析】【解答】解:20×10=200(平方米)
故答案为:B。
【分析】占地面积就是底面积,也就是长20米,宽10米的长方形面积。
2.【答案】 A
【解析】【解答】将一块正方体橡皮泥捏成长方体,正方体和长方体的体积相等,表面积不一定相等.
故答案为:A.
【分析】根据题意可知,因为将一块正方体橡皮泥捏成长方体,橡皮泥所占的空间大小不变,所以正方体和长方体的体积相等,但是形状发生了变化,所以表面积不一定相等.
3.【答案】 (1)B
(2)C
(3)A
【解析】【解答】(1)根据分析可知,表面积不变的是 ;
(2)根据分析可知, 表面积增加2 的是;
(3)根据分析可知,表面积增加4 的是.
故答案为:(1)B;(2)C;(3)A.
【分析】(1)根据表面积的定义可知,立体图形外面的面积之和叫做它的表面积,如果在顶点处挖去一个小正方体,会有3个新的面出现,与原来的3个面相等,所以表面积不变,据此判断;
(2)要求表面积增加2cm2 , 就是要比原来的表面积增加2个面,应该从某一个面的一条棱的中间部分挖,据此解答;
(3)要求表面积增加4cm2,就是要比原来的表面积增加4个面,应该从某一个面的中间部分挖,会增加4个侧面,据此解答.
4.【答案】 B
【解析】【解答】①、③都符合长方体的展开图的特点,所以都可以折叠成长方体;②的宽都在同一侧了,所以不能折成长方体;
故答案为:A。
【分析】本题考点:长方体的展开图.
此题主要考查了展开图折叠成几何体,考查同学们的空间想象能力.
由平面图形的折叠及立体图形的表面展开图的特点解题.
二、判断题
5.【答案】 错误
【解析】【解答】表面积和体积无法比较大小,原题说法错误。
故答案为:错误。
【分析】所有立体图形外面的面积之和叫做它的表面积;物件占有多少空间的量用体积表示,表面积和体积是不同的两种量,不能比较大小。
6.【答案】 正确
【解析】【解答】解:如图,
围成正方体后,A面的对面是D面,B面的对面是E面,C面的对面是F面;
因此,原题说法正确;
故答案为:正确
【分析】如图,是正方体的展开图,属于“1 4 1”结构,围成正方体后,A面的对面是D面,B面的对面是E面,C面的对面是F面.本题是考查正方体的展开图,培养学生的观察能力和空间想象能力.
7.【答案】错误
【解析】【解答】解:4×4=16,它的表面积就扩大到原来的16倍。原题说法错误。
故答案为:错误。
【分析】正方体的表面积=棱长×棱长×6,正方体表面积扩大的倍数是棱长扩大的倍数的平方倍。
三、填空题
8.【答案】 108;72
【解析】【解答】长方体的表面积:
(6×3+6×4+4×3)×2
=(18+24+12)×2
=54×2
=108(dm2)
长方体的体积:
6×4×3
=24×3
=72(dm3)
故答案为:108;72.
【分析】已知长方体的长、宽、高,求长方体的表面积,用公式:长方体的表面积=(长×宽+长×高+宽×高)×2,要求长方体的体积,用公式:长方体的体积=长×宽×高,据此列式解答.
9.【答案】 ;
【解析】【解答】根据分析可知,M与3是相对的面,M=, N与2是相对的面,N=.
故答案为:;.
【分析】根据正方体展开图的特点可知,相对的面之间一定相隔一个正方形,据此可以得到:M与3是相对的面,N与2是相对的面,根据条件“ 相对的面上的数互为倒数 ”可以求出M和N的值,据此解答.
10.【答案】 12;6;24;52
【解析】【解答】解:占地面积最大:4×3=12(平方分米),占地面积最小:3×2=6(平方分米),体积:4×3×2=24(立方分米),表面积:
(4×3+4×2+3×2)×2
=(12+8+6)×2
=26×2
=52(平方分米)
故答案为:12;6;24;52
【分析】占地面积就是底面积,根据长方体的长宽高的大小计算底面积;长方体体积=长×宽×高,长方体表面积=(长×宽+长×高+宽×高)×2。
11.【答案】 F;E
【解析】【解答】解:根据相对的面完全相同可知,A面在底部,F面在上面;F面在前面,从左面看是B面,C面是底面,那么E面是上面.
故答案为:F;E
【分析】长方体相对的面是相同的,因此从展开图中找出完全相同的面就是相对的面.
12.【答案】 100;36;100;1000
【解析】【解答】10×10=100,0.36×100=36(平方米);10×10=100,10×10×10=1000 。
故答案为:100;36;100;1000 。
【分析】从正方形面积=边长×边长可以看出,边长扩大10倍,面积扩大10×10倍;从正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长可以看出, 棱长扩大10倍,正方体的表面积扩大10×10倍,体积扩大10×10×10倍。
四、解答题
13.【答案】 解:(2×1.5+2×1.8×2+1.5×1.8×2)×20=312(平方分米)=3.12平方米
答:做20个这样的铁盒需要铁皮3.12平方米。
【解析】【分析】由题可知,将长方体的4个侧面积与一个底面积相加即可求出做一个无盖铁盒所需铁皮的面积。一个无盖铁盒所需铁皮的面积为:长×宽+长×高×2+宽×高×2,20个无盖铁盒所需铁皮的面积为:一个无盖铁盒所需铁皮的面积×20,将数值代入公式即可求出答案。注意单位的转换:1平方米=100平方分米。
14.【答案】 (1)需要3块这样的长方形和一块边长6dm的正方形。
(2)6×4×4+6×6
=96+36
=132(平方分米)
答:一共需要132平方分米的玻璃。
(3)如图:
【解析】【分析】(1)底面是正方形,那么另外四个面都得是相同的长方形,底面的边长可以是6dm,也可以是4dm;
(2)根据长方形面积的计算方法计算出这5个面的面积之和,就是一共需要玻璃的面积;
(3)设计出两个长方体,用dm作单位,长宽高的乘积在48到240之间即可。
五、综合题
15.【答案】 (1)解:60×20×(4×"")
=1200×3
=3600(立方米)
答:这个游泳池蓄水3600立方米.
(2)解:60×20+60×4×2+20×4×2
=1200+480+160
=1840(平方米)
答:贴瓷砖的面积是1840平方米.
【解析】【分析】(1)先计算出蓄水的高度,然后用底面积乘蓄水高度即可求出蓄水的体积;(2)用一个底面积加上四个侧面的面积就是需要贴瓷砖的面积.
六、应用题
16.【答案】解:20÷4=5(厘米),
5×5×20
=25×20
=500(立方厘米),
答:这个长方体的体积是500立方厘米.
【解析】【分析】根据题意可知:这个长方体的底面周长和高相等,首先用底面周长除以4求出底面边长,再根据长方体的体积公式解答即可.此题主要考查长方体的体积公式的灵活运用.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级下册数学一课一练-3.2长方体、正方体的表面积
一、单选题
1.一个长方体水池,长20米,宽10米,深2米,占地(??? )平方米。
A.?400???????????????????????????????????????B.?200???????????????????????????????????????C.?520???????????????????????????????????????D.?40
2.将一块正方体橡皮泥捏成长方体,正方体和长方体( ??)。
A.?体积相等,表面积不一定相等??????????B.?体积和表面积都不相等??????????C.?表面积相等,体积不相等
3.在一个大正方形上挖去一个棱长是1cm的小正方体,大正方体的表面积发生怎样的变化?
(1)表面积不变的是( ??)
A.??????????????????????????????B.??????????????????????????????C.?
(2)表面积增加2 的是( ??)
A.????????????????????????????????B.????????????????????????????????C.?
(3)表面积增加4 的是(? )
A.?????????????????????????B.?????????????????????????C.?
4.下列图形沿虚线折叠后能围成长方体的有(??? )。
A.?①和②???????????????????????????????B.?①和③???????????????????????????????C.?①③④???????????????????????????????D.?①②③④
二、判断题
5.棱长是6分米的正方体,它的表面积和体积相等。( ??)
6.如图围成正方体后,A面面对的是D面.
7.一个正方体的棱长扩大到原来的4倍,它的表面积就扩大到原来的8倍。
三、填空题
8.计算下列图形的表面积和体积.
表面积________? .
体积是________? .
9.右图是正方体的展开图,每个面上都填有一个数,且相对的面上的数互为倒数,则M的值是________,N的值是________。
10.一个长方体,长4分米、宽3分米、高2分米.这个长方体占地面积最大是________平方分米,占地面积最小是________平方分米;它的体积是________立方分米,表面积是________平方分米.
11.把如图所示的展开图折成一个长方体,如果A面在底部,________面在上面。如果F面在前面,从左面看是B面,那么________面在上面。
12.正方形的面积是0.36平方米.如果边长扩大10倍,正方形的面积扩大________倍,是________平方米.
正方体的棱长扩大10倍,正方体的表面积扩大________倍,体积扩大________倍
四、解答题
13.一个无盖的长方体铁盒,长是2分米,宽是1.5分米,高是1 .8分米,做20个这样的铁盒需要铁皮多少平方米?
14.黄师傅要制作一个无盖玻璃鱼缸。现在有一块长方形钢化玻璃(如下图)用作鱼缸的一个面,需要再补另外4块玻璃。
(1)要做一个底面是正方形的长方体无盖鱼缸,需要补另外4块什么尺寸的玻璃?
(2)制作第(1)题中的长方体无盖鱼缸,一共需要多少平方分米的玻璃?
(3)请你再设计两种不同的长方体鱼缸,要求鱼缸容积大于48L,小于240L。画出草图,并标出长方体鱼缸的长、宽、高。
五、综合题
15.某游泳馆有一个长60米,宽20米,深4米的游泳池。
(1)游泳池的蓄水高度为池深的 ,这个游泳池蓄水多少立方米?
(2)游泳池的底部和四壁都贴有瓷砖,贴瓷砖的面积是多少平方米?
六、应用题
16.底面是正方形的长方体包装盒高20cm,侧面展开后是一个正方形,这个长方体的体积是多少立方厘米?
参考答案
一、单选题
1.【答案】 B
【解析】【解答】解:20×10=200(平方米)
故答案为:B。
【分析】占地面积就是底面积,也就是长20米,宽10米的长方形面积。
2.【答案】 A
【解析】【解答】将一块正方体橡皮泥捏成长方体,正方体和长方体的体积相等,表面积不一定相等.
故答案为:A.
【分析】根据题意可知,因为将一块正方体橡皮泥捏成长方体,橡皮泥所占的空间大小不变,所以正方体和长方体的体积相等,但是形状发生了变化,所以表面积不一定相等.
3.【答案】 (1)B
(2)C
(3)A
【解析】【解答】(1)根据分析可知,表面积不变的是 ;
(2)根据分析可知, 表面积增加2 的是;
(3)根据分析可知,表面积增加4 的是.
故答案为:(1)B;(2)C;(3)A.
【分析】(1)根据表面积的定义可知,立体图形外面的面积之和叫做它的表面积,如果在顶点处挖去一个小正方体,会有3个新的面出现,与原来的3个面相等,所以表面积不变,据此判断;
(2)要求表面积增加2cm2 , 就是要比原来的表面积增加2个面,应该从某一个面的一条棱的中间部分挖,据此解答;
(3)要求表面积增加4cm2,就是要比原来的表面积增加4个面,应该从某一个面的中间部分挖,会增加4个侧面,据此解答.
4.【答案】 B
【解析】【解答】①、③都符合长方体的展开图的特点,所以都可以折叠成长方体;②的宽都在同一侧了,所以不能折成长方体;
故答案为:A。
【分析】本题考点:长方体的展开图.
此题主要考查了展开图折叠成几何体,考查同学们的空间想象能力.
由平面图形的折叠及立体图形的表面展开图的特点解题.
二、判断题
5.【答案】 错误
【解析】【解答】表面积和体积无法比较大小,原题说法错误。
故答案为:错误。
【分析】所有立体图形外面的面积之和叫做它的表面积;物件占有多少空间的量用体积表示,表面积和体积是不同的两种量,不能比较大小。
6.【答案】 正确
【解析】【解答】解:如图,
围成正方体后,A面的对面是D面,B面的对面是E面,C面的对面是F面;
因此,原题说法正确;
故答案为:正确
【分析】如图,是正方体的展开图,属于“1 4 1”结构,围成正方体后,A面的对面是D面,B面的对面是E面,C面的对面是F面.本题是考查正方体的展开图,培养学生的观察能力和空间想象能力.
7.【答案】错误
【解析】【解答】解:4×4=16,它的表面积就扩大到原来的16倍。原题说法错误。
故答案为:错误。
【分析】正方体的表面积=棱长×棱长×6,正方体表面积扩大的倍数是棱长扩大的倍数的平方倍。
三、填空题
8.【答案】 108;72
【解析】【解答】长方体的表面积:
(6×3+6×4+4×3)×2
=(18+24+12)×2
=54×2
=108(dm2)
长方体的体积:
6×4×3
=24×3
=72(dm3)
故答案为:108;72.
【分析】已知长方体的长、宽、高,求长方体的表面积,用公式:长方体的表面积=(长×宽+长×高+宽×高)×2,要求长方体的体积,用公式:长方体的体积=长×宽×高,据此列式解答.
9.【答案】 ;
【解析】【解答】根据分析可知,M与3是相对的面,M=, N与2是相对的面,N=.
故答案为:;.
【分析】根据正方体展开图的特点可知,相对的面之间一定相隔一个正方形,据此可以得到:M与3是相对的面,N与2是相对的面,根据条件“ 相对的面上的数互为倒数 ”可以求出M和N的值,据此解答.
10.【答案】 12;6;24;52
【解析】【解答】解:占地面积最大:4×3=12(平方分米),占地面积最小:3×2=6(平方分米),体积:4×3×2=24(立方分米),表面积:
(4×3+4×2+3×2)×2
=(12+8+6)×2
=26×2
=52(平方分米)
故答案为:12;6;24;52
【分析】占地面积就是底面积,根据长方体的长宽高的大小计算底面积;长方体体积=长×宽×高,长方体表面积=(长×宽+长×高+宽×高)×2。
11.【答案】 F;E
【解析】【解答】解:根据相对的面完全相同可知,A面在底部,F面在上面;F面在前面,从左面看是B面,C面是底面,那么E面是上面.
故答案为:F;E
【分析】长方体相对的面是相同的,因此从展开图中找出完全相同的面就是相对的面.
12.【答案】 100;36;100;1000
【解析】【解答】10×10=100,0.36×100=36(平方米);10×10=100,10×10×10=1000 。
故答案为:100;36;100;1000 。
【分析】从正方形面积=边长×边长可以看出,边长扩大10倍,面积扩大10×10倍;从正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长可以看出, 棱长扩大10倍,正方体的表面积扩大10×10倍,体积扩大10×10×10倍。
四、解答题
13.【答案】 解:(2×1.5+2×1.8×2+1.5×1.8×2)×20=312(平方分米)=3.12平方米
答:做20个这样的铁盒需要铁皮3.12平方米。
【解析】【分析】由题可知,将长方体的4个侧面积与一个底面积相加即可求出做一个无盖铁盒所需铁皮的面积。一个无盖铁盒所需铁皮的面积为:长×宽+长×高×2+宽×高×2,20个无盖铁盒所需铁皮的面积为:一个无盖铁盒所需铁皮的面积×20,将数值代入公式即可求出答案。注意单位的转换:1平方米=100平方分米。
14.【答案】 (1)需要3块这样的长方形和一块边长6dm的正方形。
(2)6×4×4+6×6
=96+36
=132(平方分米)
答:一共需要132平方分米的玻璃。
(3)如图:
【解析】【分析】(1)底面是正方形,那么另外四个面都得是相同的长方形,底面的边长可以是6dm,也可以是4dm;
(2)根据长方形面积的计算方法计算出这5个面的面积之和,就是一共需要玻璃的面积;
(3)设计出两个长方体,用dm作单位,长宽高的乘积在48到240之间即可。
五、综合题
15.【答案】 (1)解:60×20×(4×"")
=1200×3
=3600(立方米)
答:这个游泳池蓄水3600立方米.
(2)解:60×20+60×4×2+20×4×2
=1200+480+160
=1840(平方米)
答:贴瓷砖的面积是1840平方米.
【解析】【分析】(1)先计算出蓄水的高度,然后用底面积乘蓄水高度即可求出蓄水的体积;(2)用一个底面积加上四个侧面的面积就是需要贴瓷砖的面积.
六、应用题
16.【答案】解:20÷4=5(厘米),
5×5×20
=25×20
=500(立方厘米),
答:这个长方体的体积是500立方厘米.
【解析】【分析】根据题意可知:这个长方体的底面周长和高相等,首先用底面周长除以4求出底面边长,再根据长方体的体积公式解答即可.此题主要考查长方体的体积公式的灵活运用.
