北师大版七年级数学下5.3简单的轴对称图形课件(共22张ppt)
文档属性
| 名称 | 北师大版七年级数学下5.3简单的轴对称图形课件(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 9.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-15 19:48:23 | ||
图片预览





文档简介
(共22张PPT)
5.3简单的轴对称图形(1)
问题(1):轴对称有哪些性质?
知识回顾
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
请回顾等腰三角形的相关定义.
问题(2):还记得等腰三角形吗?
有两边相等的三角形叫做等腰三角形.
知识回顾
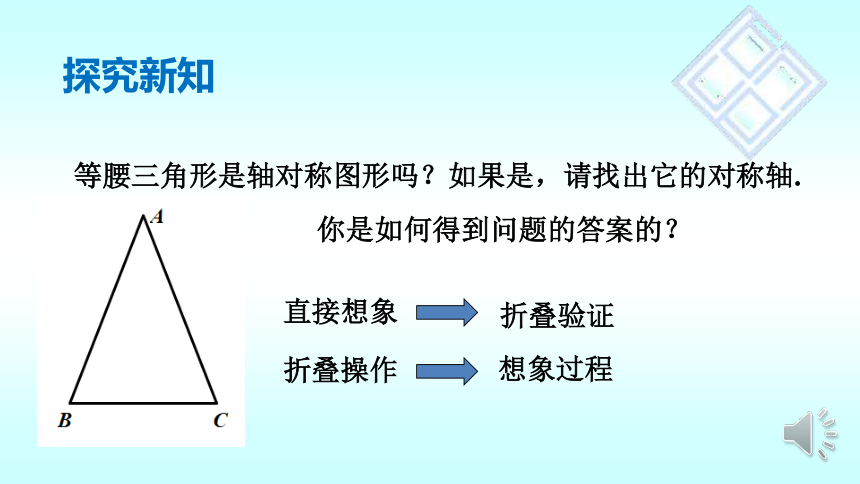
等腰三角形是轴对称图形吗?如果是,请找出它的对称轴.
探究新知
你是如何得到问题的答案的?
直接想象
折叠操作
折叠验证
想象过程
找出等腰△ABC的对称轴.
探究新知
l
等腰三角形顶角平分线所在的直线.
等腰三角形底边的中线所在的直线.
等腰三角形底边的高所在的直线.
你同意他们的观点吗?
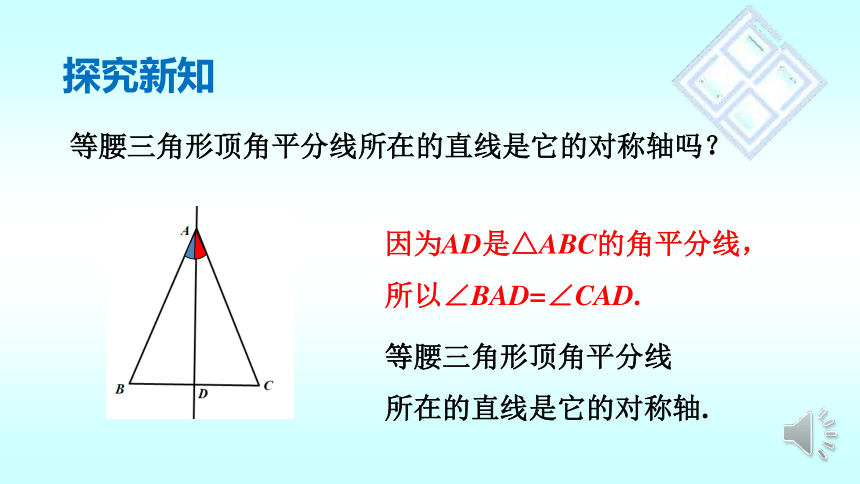
等腰三角形顶角平分线所在的直线是它的对称轴吗?
探究新知
因为AD是△ABC的角平分线,
所以∠BAD=∠CAD.
等腰三角形顶角平分线
所在的直线是它的对称轴.
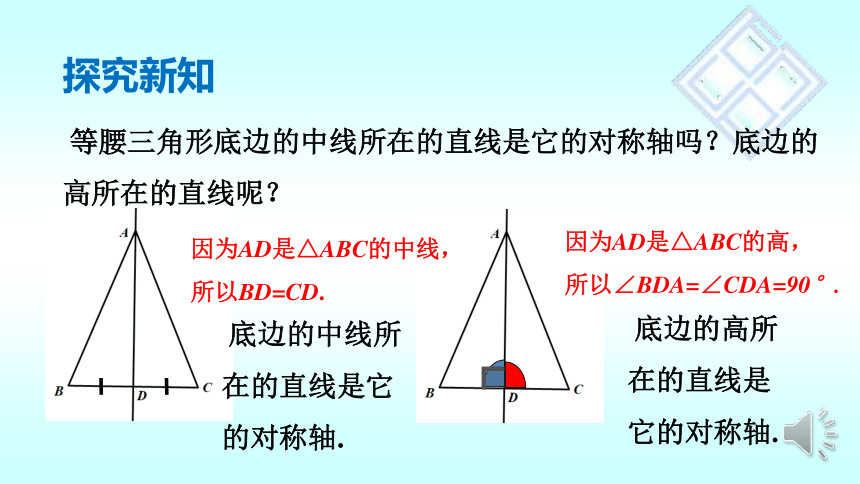
等腰三角形底边的中线所在的直线是它的对称轴吗?底边的高所在的直线呢?
探究新知
因为AD是△ABC的高,
所以∠BDA=∠CDA=90°.
因为AD是△ABC的中线,
所以BD=CD.
底边的高所在的直线是它的对称轴.
底边的中线所
在的直线是它
的对称轴.
探究新知
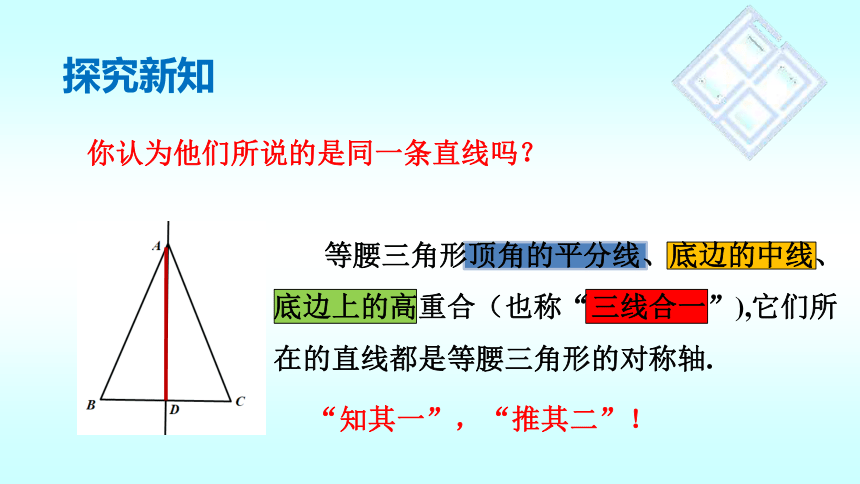
你认为他们所说的是同一条直线吗?
等腰三角形顶角的平分线、底边的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
“知其一”,“推其二”!
沿对称轴对折,你能发现等腰三角形的哪些特征?说说你的理由.
探究新知
等腰三角形的
两个底角相等.
在△ABC中
因为AB=AC,
所以∠B=∠C.
文字语言:
几何语言:
等腰三角形的性质:
阶段小结
等腰三角形的两个底角相等.
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
等腰三角形是轴对称图形.
(1)等边三角形有几条对称轴?
探究新知
直观想象或折叠操作.
等边三角形有三条对称轴.
等边三角形是特殊的等腰三角形.
探究办法:
一般到特殊!
(2)你能发现它的哪些特征?
探究新知
等边三角形每条边上的中线、高线和对角的平分线互相重合.
等边三角形是特殊的等腰三角形.
(2)你能发现它的哪些特征?
探究新知
等边三角形的三个内角都相等,且每个内角都是60°.
因为△ ABC是等边三角形,
所以∠A=∠B= ∠C=60°.
文字语言:
几何语言:
等边三角形的性质:
阶段小结
等边三角形的三个内角都相等,且每个内角都是60°.
等边三角形每条边上的中线、高线和对角的平分线互相重合.
等边三角形有三条对称轴.
你有哪些办法可以得到一个等腰三角形?
探究新知
折纸:
A
C
B
为啥呢?
你有哪些办法可以得到一个等腰三角形?
探究新知
作图:
l
A
B
轴对称
l
A
B
C
l
A
C
B
为啥呢?
1.下面是由大小不同的等边三角形组成的图案,请找出它的
对称轴.
变式练习
2.墙上钉了一根木条,小明想检验这根木条是
否水平.他拿来一个如图所示的测平仪,在这
个测平仪中,AB=AC,BC边的中点D处挂
了一个重锤.小明将BC边与木条重合,观察
此时重锤是否通过点A.如果重锤过A点,那
么这根木条就是水平的.你能说明其中的道理
吗?
变式练习
因为AB=AC,BD=CD,
所以AD⊥BC.
3.如图,在下面的等腰三角形中,∠A是顶角,分别求出它们的底角的度数.
变式练习
(1)∠B=∠C=60°
(2)∠B=∠C=45°
(3)∠B=∠C=30°
知识收获:
课堂小结
方法收获:
等腰三角形和等边三角形的性质.
从一般到特殊.
几何语言与文字语言相辅相成.
布置作业
课本:P122.习题5.3
感谢聆听!
5.3简单的轴对称图形(1)
问题(1):轴对称有哪些性质?
知识回顾
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
请回顾等腰三角形的相关定义.
问题(2):还记得等腰三角形吗?
有两边相等的三角形叫做等腰三角形.
知识回顾
等腰三角形是轴对称图形吗?如果是,请找出它的对称轴.
探究新知
你是如何得到问题的答案的?
直接想象
折叠操作
折叠验证
想象过程
找出等腰△ABC的对称轴.
探究新知
l
等腰三角形顶角平分线所在的直线.
等腰三角形底边的中线所在的直线.
等腰三角形底边的高所在的直线.
你同意他们的观点吗?
等腰三角形顶角平分线所在的直线是它的对称轴吗?
探究新知
因为AD是△ABC的角平分线,
所以∠BAD=∠CAD.
等腰三角形顶角平分线
所在的直线是它的对称轴.
等腰三角形底边的中线所在的直线是它的对称轴吗?底边的高所在的直线呢?
探究新知
因为AD是△ABC的高,
所以∠BDA=∠CDA=90°.
因为AD是△ABC的中线,
所以BD=CD.
底边的高所在的直线是它的对称轴.
底边的中线所
在的直线是它
的对称轴.
探究新知
你认为他们所说的是同一条直线吗?
等腰三角形顶角的平分线、底边的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
“知其一”,“推其二”!
沿对称轴对折,你能发现等腰三角形的哪些特征?说说你的理由.
探究新知
等腰三角形的
两个底角相等.
在△ABC中
因为AB=AC,
所以∠B=∠C.
文字语言:
几何语言:
等腰三角形的性质:
阶段小结
等腰三角形的两个底角相等.
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
等腰三角形是轴对称图形.
(1)等边三角形有几条对称轴?
探究新知
直观想象或折叠操作.
等边三角形有三条对称轴.
等边三角形是特殊的等腰三角形.
探究办法:
一般到特殊!
(2)你能发现它的哪些特征?
探究新知
等边三角形每条边上的中线、高线和对角的平分线互相重合.
等边三角形是特殊的等腰三角形.
(2)你能发现它的哪些特征?
探究新知
等边三角形的三个内角都相等,且每个内角都是60°.
因为△ ABC是等边三角形,
所以∠A=∠B= ∠C=60°.
文字语言:
几何语言:
等边三角形的性质:
阶段小结
等边三角形的三个内角都相等,且每个内角都是60°.
等边三角形每条边上的中线、高线和对角的平分线互相重合.
等边三角形有三条对称轴.
你有哪些办法可以得到一个等腰三角形?
探究新知
折纸:
A
C
B
为啥呢?
你有哪些办法可以得到一个等腰三角形?
探究新知
作图:
l
A
B
轴对称
l
A
B
C
l
A
C
B
为啥呢?
1.下面是由大小不同的等边三角形组成的图案,请找出它的
对称轴.
变式练习
2.墙上钉了一根木条,小明想检验这根木条是
否水平.他拿来一个如图所示的测平仪,在这
个测平仪中,AB=AC,BC边的中点D处挂
了一个重锤.小明将BC边与木条重合,观察
此时重锤是否通过点A.如果重锤过A点,那
么这根木条就是水平的.你能说明其中的道理
吗?
变式练习
因为AB=AC,BD=CD,
所以AD⊥BC.
3.如图,在下面的等腰三角形中,∠A是顶角,分别求出它们的底角的度数.
变式练习
(1)∠B=∠C=60°
(2)∠B=∠C=45°
(3)∠B=∠C=30°
知识收获:
课堂小结
方法收获:
等腰三角形和等边三角形的性质.
从一般到特殊.
几何语言与文字语言相辅相成.
布置作业
课本:P122.习题5.3
感谢聆听!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
