沪科版七上数学第4章4.3线段的长短比较 习题课件(28张PPT)
文档属性
| 名称 | 沪科版七上数学第4章4.3线段的长短比较 习题课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 682.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 12:41:43 | ||
图片预览







文档简介
(共28张PPT)
4.3 线段的长短比较
第4章 直线与角
答案显示
相等;BM;AB;BM;AM
A
C
A
B
核心必知
基础巩固练
长度
答案显示
2
D
能力提升练
变短;两点之间线段最短
B
D
C
答案显示
5 cm或1 cm.图略.
EF的长为12 cm.
(1)MN=8.(2)2.(3)存在点P,使点P到点M,N的距离之和是10.点P的位置可分为以下两种情况:x=-3.x=7.
答案显示
素养核心练
1.在线段上并且把该线段分成________的两条线段的点,叫做线段的中点.若点M是线段AB的中点,则有AM=________=________,或AB=2________=2________.但若AM=BM,点M未必是AB的中点.
2.两点之间线段的________,叫做这两点之间的距离;两点间的距离是一个数,它不是线段.
相等
BM
AB
BM
AM
长度
1.下列图形中能比较长短的是( )
A.两条线段 B.两条直线
C.直线与射线 D.两条射线
A
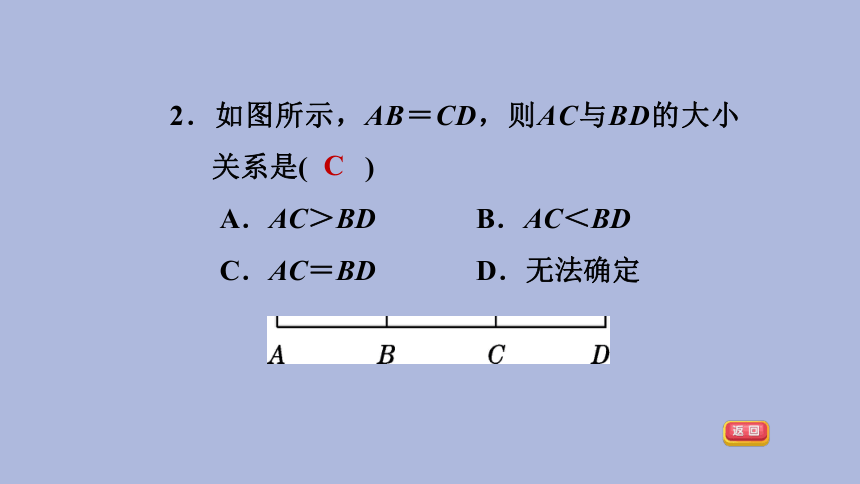
2.如图所示,AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD
C.AC=BD D.无法确定
C
3.[期末·合肥庐阳区]如图,下列等式不一定成立的是( )
A.AC-BC=BD-BC B.AD-CD=AB+BC
C.AC-BC=AD-BD D.AD-AC=BD-BC
A
B
5.[期末·合肥瑶海区]如图,C,D是线段AB延长线上两点,若CD=4 cm,DB=7 cm,且B是AC的中点,则AC的长等于( )
A.3 cm B.6 cm
C.11 cm D.14 cm
B
6.[期末·阜阳太和县]如图,点C是线段AB的中点,AB=6 cm,如果点D是线段AB上一点,且BD=1 cm,那么CD=________cm.
2
7.点B在直线AC上,线段AB=5,BC=3,则A,C两点间的距离是( )
A.8 B.2
C.8或2 D.无法确定
C
8.[中考·徐州]点A,B,C在同一数轴上,其中点A,B表示的数分别为-3,1,若BC=2,则AC等于( )
A.3 B.2 C.3或5 D.2或6
D
9.[期末·芜湖南陵县]如图,我们可以把弯曲的河道改直,改直后A,B两地间的河道长度会________(填“变短”“变长”或“不变”),数学依据是_______________________.
变短
两点之间线段最短
10.[期末·芜湖]从点O引两条射线OA,OB,在OA,OB上分别截取OM=1 cm,ON=1 cm,则M,N两点间的距离一定( )
A.小于1 cm B.大于1 cm
C.等于1 cm D.有最大值2 cm
D
11.[期末·芜湖]如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.AC=3 cm,CP=1 cm,线段PN=________cm.
12.[期末·安庆宿松县]已知点B在直线AC上,AB=4 cm,AC=6 cm,P,Q分别是AB,AC的中点,求线段PQ的长.
①
②
13.[期末·六安舒城县]如图,A,B是线段EF上两点,已知EA : AB : BF=1 : 2 : 3,M,N分别为EA,BF的中点,且MN=8 cm,求EF的长.
14.[2018·阜阳九中期末]如图,已知数轴上M,O,N三点对应的数分别为-2,0,6,点P为数轴上任意一点,其对应的数为x.
(1)求MN的长;
(2)若点P是MN的中点,则x的值是________;
(3)数轴上是否存在一点P,使点P到点M,N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.
解:MN=8.
2
解:存在点P,使点P到点M,N的距离之和是10.
因为MN=8,所以点P的位置可分为以下两种情况:
①当点P在点M的左边时,PN+PM=6-x+(-2-x)=10,解得x=-3.
②当点P在点N的右边时,PN+PM=x-6+x-(-2)=10,解得x=7.
15.如图,若线段AB=20 cm,点C是线段AB上一点,M,N分别是线段AC,BC的中点.
(1)求线段MN的长;
15.如图,若线段AB=20 cm,点C是线段AB上一点,M,N分别是线段AC,BC的中点.
(2)根据(1)中的计算过程和结果,设AB=a,其他条件不变,你能猜出MN的长度吗?请用一句简洁的话表达你发现的规律.
16.[2018·合肥瑶海区期末]如图①,点C在线段AB上,图中共有三条线段AB,AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“2倍点”.
(1)线段的中点________这条线段的“2倍点”(填“是”或“不是”);
是
16.[2018·合肥瑶海区期末]如图①,点C在线段AB上,图中共有三条线段AB,AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“2倍点”.
(2)若AB=15 cm,点C是线段AB的“2倍点”,求AC的长;
(3)如图②,已知AB=20 cm.动点P从点A出发,以2 cm/s的速度沿AB向点B匀速移动.点Q从点B出发,以1 cm/s的速度沿BA向点A匀速移动.点P,Q同时出发,当其中一点到达终点时,移动停止,设移动的时间为t(s),当t=________s时,点Q恰好是线段AP的“2倍点”(请直接写出答案).
4.3 线段的长短比较
第4章 直线与角
答案显示
相等;BM;AB;BM;AM
A
C
A
B
核心必知
基础巩固练
长度
答案显示
2
D
能力提升练
变短;两点之间线段最短
B
D
C
答案显示
5 cm或1 cm.图略.
EF的长为12 cm.
(1)MN=8.(2)2.(3)存在点P,使点P到点M,N的距离之和是10.点P的位置可分为以下两种情况:x=-3.x=7.
答案显示
素养核心练
1.在线段上并且把该线段分成________的两条线段的点,叫做线段的中点.若点M是线段AB的中点,则有AM=________=________,或AB=2________=2________.但若AM=BM,点M未必是AB的中点.
2.两点之间线段的________,叫做这两点之间的距离;两点间的距离是一个数,它不是线段.
相等
BM
AB
BM
AM
长度
1.下列图形中能比较长短的是( )
A.两条线段 B.两条直线
C.直线与射线 D.两条射线
A
2.如图所示,AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD
C.AC=BD D.无法确定
C
3.[期末·合肥庐阳区]如图,下列等式不一定成立的是( )
A.AC-BC=BD-BC B.AD-CD=AB+BC
C.AC-BC=AD-BD D.AD-AC=BD-BC
A
B
5.[期末·合肥瑶海区]如图,C,D是线段AB延长线上两点,若CD=4 cm,DB=7 cm,且B是AC的中点,则AC的长等于( )
A.3 cm B.6 cm
C.11 cm D.14 cm
B
6.[期末·阜阳太和县]如图,点C是线段AB的中点,AB=6 cm,如果点D是线段AB上一点,且BD=1 cm,那么CD=________cm.
2
7.点B在直线AC上,线段AB=5,BC=3,则A,C两点间的距离是( )
A.8 B.2
C.8或2 D.无法确定
C
8.[中考·徐州]点A,B,C在同一数轴上,其中点A,B表示的数分别为-3,1,若BC=2,则AC等于( )
A.3 B.2 C.3或5 D.2或6
D
9.[期末·芜湖南陵县]如图,我们可以把弯曲的河道改直,改直后A,B两地间的河道长度会________(填“变短”“变长”或“不变”),数学依据是_______________________.
变短
两点之间线段最短
10.[期末·芜湖]从点O引两条射线OA,OB,在OA,OB上分别截取OM=1 cm,ON=1 cm,则M,N两点间的距离一定( )
A.小于1 cm B.大于1 cm
C.等于1 cm D.有最大值2 cm
D
11.[期末·芜湖]如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.AC=3 cm,CP=1 cm,线段PN=________cm.
12.[期末·安庆宿松县]已知点B在直线AC上,AB=4 cm,AC=6 cm,P,Q分别是AB,AC的中点,求线段PQ的长.
①
②
13.[期末·六安舒城县]如图,A,B是线段EF上两点,已知EA : AB : BF=1 : 2 : 3,M,N分别为EA,BF的中点,且MN=8 cm,求EF的长.
14.[2018·阜阳九中期末]如图,已知数轴上M,O,N三点对应的数分别为-2,0,6,点P为数轴上任意一点,其对应的数为x.
(1)求MN的长;
(2)若点P是MN的中点,则x的值是________;
(3)数轴上是否存在一点P,使点P到点M,N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.
解:MN=8.
2
解:存在点P,使点P到点M,N的距离之和是10.
因为MN=8,所以点P的位置可分为以下两种情况:
①当点P在点M的左边时,PN+PM=6-x+(-2-x)=10,解得x=-3.
②当点P在点N的右边时,PN+PM=x-6+x-(-2)=10,解得x=7.
15.如图,若线段AB=20 cm,点C是线段AB上一点,M,N分别是线段AC,BC的中点.
(1)求线段MN的长;
15.如图,若线段AB=20 cm,点C是线段AB上一点,M,N分别是线段AC,BC的中点.
(2)根据(1)中的计算过程和结果,设AB=a,其他条件不变,你能猜出MN的长度吗?请用一句简洁的话表达你发现的规律.
16.[2018·合肥瑶海区期末]如图①,点C在线段AB上,图中共有三条线段AB,AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“2倍点”.
(1)线段的中点________这条线段的“2倍点”(填“是”或“不是”);
是
16.[2018·合肥瑶海区期末]如图①,点C在线段AB上,图中共有三条线段AB,AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“2倍点”.
(2)若AB=15 cm,点C是线段AB的“2倍点”,求AC的长;
(3)如图②,已知AB=20 cm.动点P从点A出发,以2 cm/s的速度沿AB向点B匀速移动.点Q从点B出发,以1 cm/s的速度沿BA向点A匀速移动.点P,Q同时出发,当其中一点到达终点时,移动停止,设移动的时间为t(s),当t=________s时,点Q恰好是线段AP的“2倍点”(请直接写出答案).
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
