湘教版八年级数学下册第二章 四边形 单元练习(含答案)
文档属性
| 名称 | 湘教版八年级数学下册第二章 四边形 单元练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 613.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-15 20:35:03 | ||
图片预览




文档简介
第二章 四边形
一、单选题
1.六边形的内角和为( )
A.720° B.360° C.540° D.180°
2.如图,的对角线,交于点,,,,那么的长为( )
A. B. C.3 D.4
3.如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
A.AB=CD B.AD∥BC C.OA=OC D.AD=BC
4.窗棂即窗格(窗里面的横的或竖的格)是中国传统木构建筑的框架结构设计,窗棂上雕刻有线槽和各种花纹,构成种类繁多的优美图案.下列表示我国古代窗棂样式结构图案中,是中心对称图形但不是轴对称图形的是( )
A. B.
C. D.
5.如图,平行四边形ABCD的周长是32cm,△ABC的周长是26cm,E、F分别是边AB、BC的中点,则EF的长为( )
A.8cm B.6cm C.5cm D.4cm
6.矩形的边长是,一条对角线的长是,则矩形的面积是( )
A. B. C.. D.
7.如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点,若,,则FC的长度为
A.1 B.2 C. D.
8.如图,菱形中,是的垂直平分线,,则等于( )
A. B. C. D.
9.下列命题正确的是( )
A.对角线互相垂直且相等的四边形是菱形
B.一组对边平行,一组邻角互补的四边形是平行四边形
C.对角线相等的四边形是矩形
D.等腰梯形的两条对角线相等
10.如图,分别以的直角边和斜边为边向外作正方形和正方形,连结、、.给出下列结论:
①;
②
③
④其中正确的是( )
A.②③④ B.①②③ C.①②④ D.①②③④
二、填空题
11.若一个正多边形的内角是外角的3倍还多20°,则这个多边形的边数是__________.
12.在?ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F,若AD=11,EF=5,则AB=_____.
13.如图,把一张长方形纸条按图中那样折叠后,若得到∠AOB′=70°,则∠OGC=__.
14.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得,接着活动学具成为图2所示正方形,并测得正方形的对角线,则图1中对角线AC的长为_____.
三、解答题
15.一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.
(1)求这个多边形是几边形;
(2)求这个多边形的每一个内角的度数.
16.如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.
(1)求BC的长;
(2)若∠CBE=36°,求∠ADC.
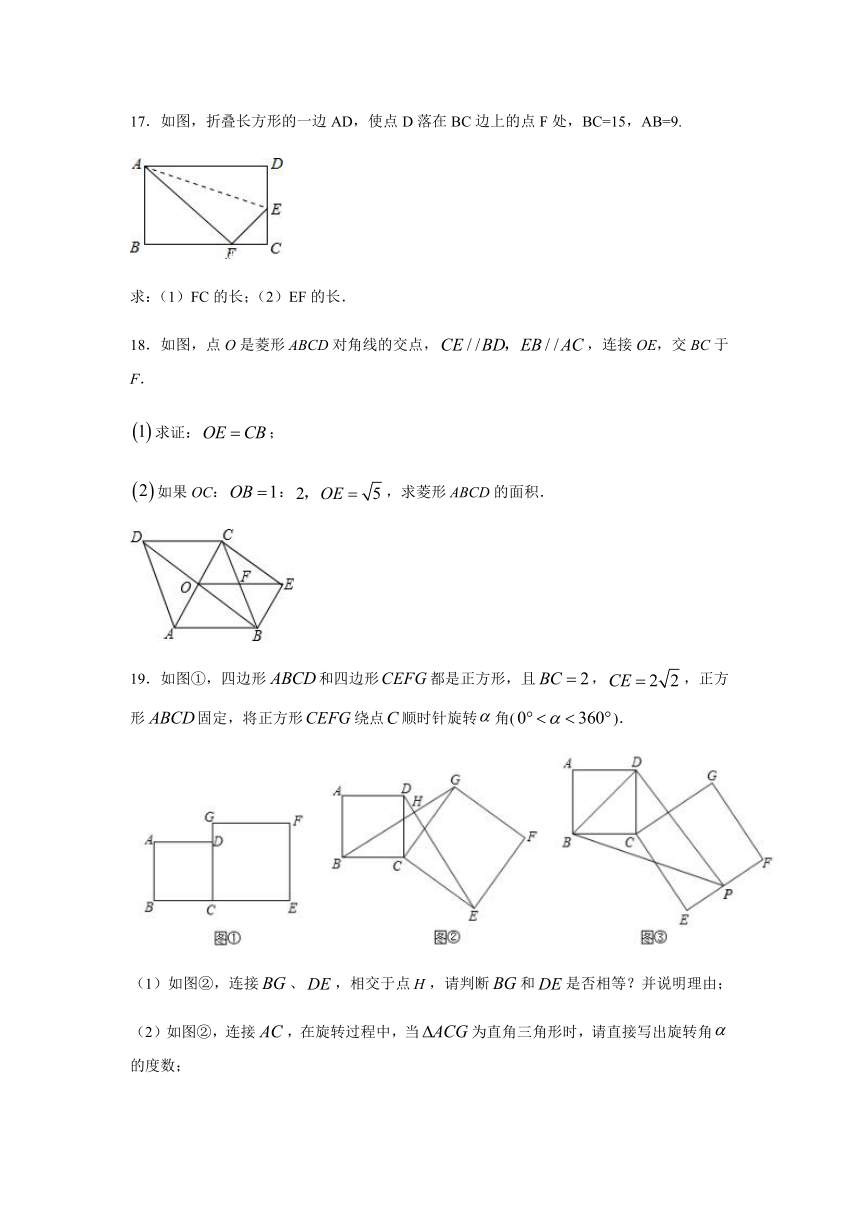
17.如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=15,AB=9.
求:(1)FC的长;(2)EF的长.
18.如图,点O是菱形ABCD对角线的交点,,连接OE,交BC于F.
求证:;
如果OC::,求菱形ABCD的面积.
19.如图①,四边形和四边形都是正方形,且,,正方形固定,将正方形绕点顺时针旋转角().
(1)如图②,连接、,相交于点,请判断和是否相等?并说明理由;
(2)如图②,连接,在旋转过程中,当为直角三角形时,请直接写出旋转角的度数;
(3)如图③,点为边的中点,连接、、,在正方形的旋转过程中,的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由
答案
1.A
2.D
3.D
4. A
5.C
6.C
7.A
8.A
9.D
10.C
11.9
12.8或3
13.125°
14.
15.(1)设内角为x,则外角为,
由题意得,x+ =180°,
解得:x=120°,
=60°,
这个多边形的边数为:=6,
答:这个多边形是六边形,
(2)设内角为x,则外角为,
由题意得: x+ =180°,
解得:x=120°,
答:这个多边形的每一个内角的度数是120度.
内角和=(6﹣2)×180°=720°.
16.解:(1)∵四边形ABCD是平行四边形,
∴AD=BC,DC∥AB,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DAE=∠DEA,
∴AD=DE=10,
∴BC=10;
(2)∵CE=6,BE=8,BC=10,
∴CE2+BE2=62+82=100=BC2,
∴△BCE是直角三角形,且∠BEC=90°,
∴∠C=90°﹣∠CBE=90°﹣36°=54°,
∵AD∥BC,
∴∠D=180°﹣∠C=180°﹣54°=126°.
17.解:(1)∵矩形对边相等,
∴AD=BC=15
∵折叠长方形的一边AD,点D落在BC边上的点F处
∴AF=AD=15,
在Rt△ABF中,由勾股定理得,
∴FC=BC·BF=15-12=3
(2)折叠长方形的一边AD,点D落在BC边上的点F处
∴EF=DE
设DE=x,则EC=9·x,
在Rt△EFC中,由勾股定理得,
即
解得x=5
即EF的长为5。
18.四边形ABCD是菱形,
.
,
四边形OCEB是平行四边形,
四边形OCEB是矩形,
;
由知,::2,
.
在中,由勾股定理得,
.
四边形ABCD是菱形,
,
菱形ABCD的面积是:.
19.(1)证明:相等
∵四边形和四边形都是正方形,
∴,,,
∴,即,
∴;
∴BG=DE
(2)如图1,∠ACG=90°时,旋转角;
如图2,当∠ACG=90°时,旋转角;
综上所述,旋转角的度数为45°或225°;
(3)存在
∵如图3,在正方形中,,
∴,
∴当点到的距离最远时,的面积最大,
作,连接,,则
当三点共线时,最大,此时的面积最大.
∵,点为的中点,
∴
此时,,
∴.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
