2020年中考数学三轮易错复习:专题18 利用函数图象研究函数性质及新题型(解析版)
文档属性
| 名称 | 2020年中考数学三轮易错复习:专题18 利用函数图象研究函数性质及新题型(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 613.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-15 00:00:00 | ||
图片预览




文档简介
2020年中考数学三轮易错复习:专题18 利用函数图象研究函数性质及新题型
【例1】(2019·开封模拟)参照学习函数的过程与方法,探究函数(x≠0)的图象与性质.
因为,即,所以我们对比函数来探究.
列表:
x
…
-4
-3
-2
-1
1
2
3
4
…
…
1
2
4
-4
-2
-1
…
…
2
3
5
-3
-1
0
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来.
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而__________;(填“增大”或“减小”)
②的图象是由的图象向_______平移______个单位而得到;
③图象关于点__________中心对称.(填点的坐标)
(3)函数与直线y=-2x+1交于点A,B,求△AOB的面积.
【变式1-1】(2019·郑州模拟)探究函数的图象与性质
(1)函数的自变量x的取值范围是 ;
(2)下列四个函数图象中可能是函数的图象的是
(3)对于函数,当x>0时,求y的取值范围.
解:∵x>0,
∴==+ ,
∵≥0,
∴y≥ .
拓展运用
(4)若函数,则y的取值范围是 .
【例2】(2018·洛阳三模)在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”. 有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
已知抛物线与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,点A的坐标为 ,点B的标为 ;
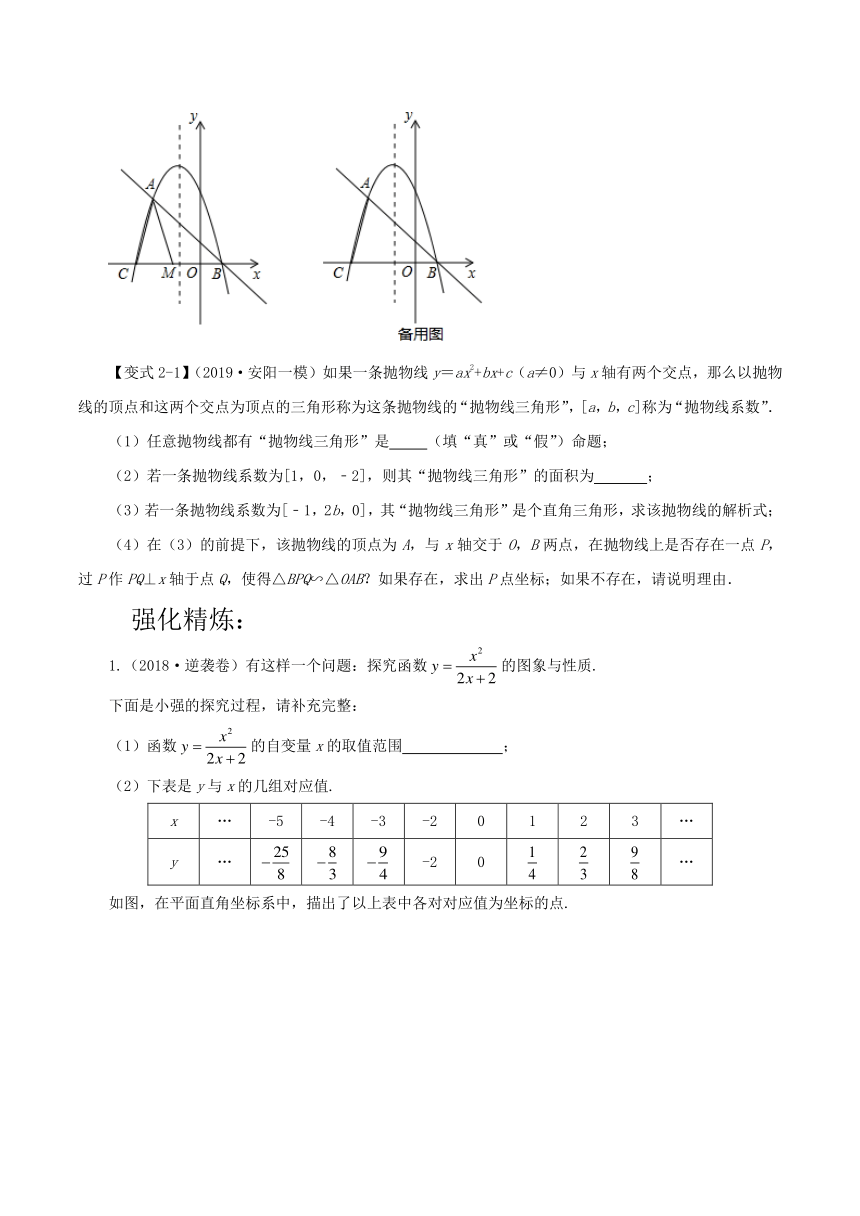
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
【变式2-1】(2019·安阳一模)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线系数”.
(1)任意抛物线都有“抛物线三角形”是 (填“真”或“假”)命题;
(2)若一条抛物线系数为[1,0,﹣2],则其“抛物线三角形”的面积为 ;
(3)若一条抛物线系数为[﹣1,2b,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;
(4)在(3)的前提下,该抛物线的顶点为A,与x轴交于O,B两点,在抛物线上是否存在一点P,过P作PQ⊥x轴于点Q,使得△BPQ∽△OAB?如果存在,求出P点坐标;如果不存在,请说明理由.
强化精炼:
1.(2018·逆袭卷)有这样一个问题:探究函数的图象与性质.
下面是小强的探究过程,请补充完整:
(1)函数的自变量x的取值范围 ;
(2)下表是y与x的几组对应值.
x
…
-5
-4
-3
-2
0
1
2
3
…
y
…
-2
0
…
如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.
①观察图中各点的位置发现:点A1和B1,点A2和B2,A3和B3,A4和B4均关于某点中心对称,则该点的坐标为 ;
②小文分析函数的表达式发现:当x<-1时,函数的最大值为-2,则该函数图象在直线x=-1左侧的最高点的坐标为
(3)画出该函数的图象,并写出该函数的一条性质
2.(2019·偃师一模)如图,抛物线y=ax2+bx+4(a≠0)交x轴于点A(4,0),B(-2,0),交y轴于点C.
(1)求抛物线的解析式.
(2)点 Q 是 x 轴上位于点A,B之间的一个动点,点E为线段BC上一个动点,若始终保持∠EQB=∠CAB,连接CQ,设△CQE 的面积为S,点Q的横坐标为m,求出S关于m的函数关系式,并求出当S取最大值时点Q的坐标.
(3)点 P 为抛物线上位于 AC 上方的一个动点,过点 P 作 PF⊥y 轴,交直线 AC 于点 F,点 D 的坐标为(2,0),若 O,D,F 三点中,当其中一点恰好 位于另外两点的垂直平分线上时,我们把这个点叫做另外两点的“和谐点”,请判断这三点是否有“和谐点”的存在,若存在,请直接写出此时点P的坐标;若不存在,请说明理由.
3.(2019·三门峡二模)定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,﹣3),C(﹣1,﹣5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为( )
A.(1,﹣2) B.(2,﹣1) C.(,﹣1) D.(3,0)
4.(2019·开封模拟)【阅读理解】
截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD,连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是 ;
【拓展延伸】
(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;
【知识应用】
(3)如图3,两块斜边长都为14cm的三角板,把斜边重叠摆放在一起,则两块三角板的直角顶点之间的距离PQ的长分别为 cm.
图1 图2 图3
5.(2019·郑州联考)如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明:
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸:
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
图1 图2
6.(2019·平顶山三模)已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β,
(1)如图1,若点D在线段BC上,点E在线段AC上.∠ABC=60°,∠ADE=70°,则α= °;β= °.
(2)如图2,若点D在线段BC上,点E在线段AC上,则α,β之间有什么关系式?说明理由.
(3)是否存在不同于(2)中的α,β之间的关系式?若存在,请写出这个关系式(写出一种即可),说明理由;若不存在,请说明理由.
图1 图2
7.(2019·郑州外国语模拟)如图,在平面直角坐标系xOy中,直线y=kx+k与双曲线(x>0)交于点A(1,a).
(1)求a,k的值;
(2)已知直线l过点D(2,0)且平行于直线y=kx+k,点P(m,n),(m>3)是直线l上一动点,过点P作坐标轴的平行线,交双曲线于点M、N,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为W. 横、纵坐标都是整数的点叫做整点.
①当m=4时,直接写出区域W内的整点个数;
②若区域W内的整点个数正好是8个,结合图象,求m的取值范围.
8.(2019·郑州外国语模拟)如图,一段抛物线y=-x2+4(-2≤x≤2)为C1,与x轴交于A0、A1两点,顶点为D1;将C1绕点A1选择180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t= x1+x2+x3,则t的取值范围是( )
A. 69.(2019·南阳二模)如图,在 8×8 的网格中,每个小方格都是边长为 1 的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于 y 轴的抛物线与网格对角线 OM 的两个交点为 A,B,其顶点为 C,如果△ABC 是该抛物线的内接格点三角形,且 AB=,点 A,B,C 的横坐标 xA,xB,xC 满足 xA<xC<xB,那么符合上述条件的抛物线的条数是 .
10.(2017?禹州市二模)有这样一个问题:探究函数y=x2+的图象与性质,小东根据学习函数的经验,对函数y=x2+的图象与性质进行了探究,下面是小东的探究过程,请补充完整:
(1)下表是y与x的几组对应值.
x
…
﹣3
﹣2
﹣1
1
2
3
…
y
…
m
…
函数y=x2+的自变量x的取值范围是 ,m的值为 ;
(2)在如图所示的平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并画出该函数的大致图象;
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程x2+=0有 个实数根;
②方程x2+=2有 个实数根;
③结合函数的图象,写出该函数的一条性质 .
2020年中考数学三轮易错复习:专题18 利用函数图象研究函数性质及新题型
【例1】(2019·开封模拟)参照学习函数的过程与方法,探究函数(x≠0)的图象与性质.
因为,即,所以我们对比函数来探究.
列表:
x
…
-4
-3
-2
-1
1
2
3
4
…
…
1
2
4
-4
-2
-1
…
…
2
3
5
-3
-1
0
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来.
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而__________;(填“增大”或“减小”)
②的图象是由的图象向_______平移______个单位而得到;
③图象关于点__________中心对称.(填点的坐标)
(3)函数与直线y=-2x+1交于点A,B,求△AOB的面积.
【答案】(1)见解析;(2)增大;上,1;(0,1);(3)见解析.
【解析】解:(1)如图所示;
(2)①增大;②上,1;③(0,1);
(3)联立:与直线y=-2x+1,
解得:x=1,y=-1或x=-1,y=3,
∴S△AOB=×2×4-×1×4-×2×1=1.
【变式1-1】(2019·郑州模拟)探究函数的图象与性质
(1)函数的自变量x的取值范围是 ;
(2)下列四个函数图象中可能是函数的图象的是
(3)对于函数,当x>0时,求y的取值范围.
解:∵x>0,
∴==+ ,
∵≥0,
∴y≥ .
拓展运用
(4)若函数,则y的取值范围是 .
【答案】(1)x≠0;(2)C;(3)4,4;(4)y≥1或y≤-11.
【解析】解:(1)由分式的意义,知x≠0;
(2)∵x≠0,
∴A错误;
当x>0时,y>0,故B、D错误,
∴选项C正确;
(3)4;4;
(4)当x>0时,==
∵≥0,
∴y≥1;
当x<0时,
=
=,
∵≤0
∴y≤-11;
综上所述,y≥1或y≤-11.
【例2】(2018·洛阳三模)在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”. 有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
已知抛物线与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,点A的坐标为 ,点B的标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
【答案】(1),(-2,),(1,0);(2)(3)见解析.
【解析】解:(1)抛物线,由定义知:
其梦想直线的解析式为:,
联立,,解得:
或,
故答案为:,(-2,),(1,0).
(2)由题意知C(-3,0),过A作AG⊥y轴于G,
①当点N在y轴上时,△AMN是梦想三角形,
AC=AN=,
由抛物线的对称轴x=-1,A(-2,),得:AG=2,G(0,),
在Rt△ANG中,由勾股定理得:
GN=3,
∴N(0,+3)或(0,-3),
当ON=+3时,则MN>OG>CM,与MN=CM矛盾,不合题意,
∴N(0,-3),
②当点M在y轴上时,△AMN为梦想三角形,
即M点在坐标原点,M(0,0),
在Rt△AGM中, AG=2,GM=,tan∠AMG=,
∴∠AMG=30°,
∴∠AMC=∠AMN=∠NMB=60°,
过点N作NP⊥x轴,
在Rt△NMP中,MN=CM=3,
∴NP=,OP=,即N(,),
综上所述,点N的坐标为(0,-3),(,).
(3)设E(-1,m),F(n,),
∵A(-2,),C(-3,0),
①当四边形ACEF是平行四边形时,有:
,
解得:,
即E(-1,),F(0,);
②当四边形AECF是平行四边形时,有:
,
解得:,
即E(-1,),F(-4,);
③当四边形AEFC是平行四边形时,有:
,
解得:,
此时F与A重合,不符题意,舍去;
综上所述,E(-1,),F(-4,)或E(-1,),F(0,).
【变式2-1】(2019·安阳一模)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线系数”.
(1)任意抛物线都有“抛物线三角形”是 (填“真”或“假”)命题;
(2)若一条抛物线系数为[1,0,﹣2],则其“抛物线三角形”的面积为 ;
(3)若一条抛物线系数为[﹣1,2b,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;
(4)在(3)的前提下,该抛物线的顶点为A,与x轴交于O,B两点,在抛物线上是否存在一点P,过P作PQ⊥x轴于点Q,使得△BPQ∽△OAB?如果存在,求出P点坐标;如果不存在,请说明理由.
【答案】(1)假;(2);(3)(4)见解析.
【解析】解:(1)∵抛物线与x轴的交点个数有三种情况:没交点,一个交点,两个交点,
∴任意抛物线都有“抛物线三角形”是假命题,
故答案为:假;
(2)∵一条抛物线系数为[1,0,﹣2],
∴a=1,b=0,c=﹣2,
∴抛物线解析式为y=x2﹣2,
当x=0,y=﹣2,
当y=0,解得,x=,
∴“抛物线三角形”的面积为×(+)×2=2
故答案为:2.
(3)由题意得:抛物线解析式为:y=﹣x2+2bx,
与x轴交点为:(0,0),(2b,0);
若“抛物线三角形”是个直角三角形,则是等腰直角三角形,
∴顶点为(b,b)或(b,﹣b),
①当顶点为(b,b)时,
有:b=﹣b2+2b2,
解得b=0(舍去)或b=1
∴y=﹣x2+2x,
②当顶点为(b,﹣b)时,
有:﹣b=﹣b2+2b2,
解得b=0(舍去)或b=﹣1
∴y=﹣x2﹣2x,
(4)∵△AOB为等腰直角三角形,且△BPQ∽△OAB,
∴△BPQ为等腰直角三角形,
①y=﹣x2+2x,
设P(a,﹣a2+2a),
则Q(a,0)
则|﹣a2+2a|=|2﹣a|,
解得:a=1(舍)或a=2(舍去)或a=-1,
∴P(﹣1,﹣3);
②y=﹣x2﹣2x,
同理得:P(1,3);
综上所述,点P(﹣1,﹣3)或(1,3).
强化精炼:
1.(2018·逆袭卷)有这样一个问题:探究函数的图象与性质.
下面是小强的探究过程,请补充完整:
(1)函数的自变量x的取值范围 ;
(2)下表是y与x的几组对应值.
x
…
-5
-4
-3
-2
0
1
2
3
…
y
…
-2
0
…
如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.
①观察图中各点的位置发现:点A1和B1,点A2和B2,A3和B3,A4和B4均关于某点中心对称,则该点的坐标为 ;
②小文分析函数的表达式发现:当x<-1时,函数的最大值为-2,则该函数图象在直线x=-1左侧的最高点的坐标为
(3)画出该函数的图象,并写出该函数的一条性质
【答案】(1)x≠-1;(2)①(-1,-1);②(-2,-2);(3)见解析.
【解析】解:(1)由2x+2≠0得,x≠-1;
(2)①由图象知,该点坐标为:(-1,-1);
②当x=-2时,y=-2,∴图象在直线x=-1左侧的最高点的坐标为(-2,-2);
③图象见下图.
函数性质:函数图象不经过第四象限;当x<-2时,y随x的增大而增大;当-20时,y随x的增大而增大;当-12.(2019·偃师一模)如图,抛物线y=ax2+bx+4(a≠0)交x轴于点A(4,0),B(-2,0),交y轴于点C.
(1)求抛物线的解析式.
(2)点 Q 是 x 轴上位于点A,B之间的一个动点,点E为线段BC上一个动点,若始终保持∠EQB=∠CAB,连接CQ,设△CQE 的面积为S,点Q的横坐标为m,求出S关于m的函数关系式,并求出当S取最大值时点Q的坐标.
(3)点 P 为抛物线上位于 AC 上方的一个动点,过点 P 作 PF⊥y 轴,交直线 AC 于点 F,点 D 的坐标为(2,0),若 O,D,F 三点中,当其中一点恰好 位于另外两点的垂直平分线上时,我们把这个点叫做另外两点的“和谐点”,请判断这三点是否有“和谐点”的存在,若存在,请直接写出此时点P的坐标;若不存在,请说明理由.
【答案】见解析.
【解析】解:(1)∵y=ax2+bx+4交x轴于点A(4,0),B(-2,0),
∴,
解得:a=,b=1,
∴抛物线的解析式为:y=x2+x+4.
(2)y=x2+x+4与y轴交于点C,
∴C(0,4),
∵A(4,0),B(-2,0),
设直线AC的解析式为:y=kx+n,
∴4k+n=0,n=4,
解得:k=-1,n=4,
即直线AC的解析式:y=-x+4,
同理得:直线BC的解析式为:y=2x+4,
∵∠EQB=∠CAB,
∴EQ∥AC,
∵点Q的坐标为(m,0),
设直线EQ解析式为:y=-x+m,
联立:y=-x+m,y=2x+4解得:
x=,y=,
即E(,),
设直线EQ交y轴于点H,
如下图所示,
∴S=·CH·|xE-xQ|
=,其中:-2∵<0,
∴当m=1时,S取最大值,此时Q点坐标为(1,0).
(3)存在,理由如下,如下图所示,
和谐点为O(0,0),D(2,0),设F(x,-x+4),
①若O是和谐点,
则OF=OD=2,
即:OF2=OD2=4,
x2+(-x+4)2=4,此方程无实数解,即O不是和谐点;
②若D是和谐点,
同理:OD=DF=2,
即:(2-x)2+(-x+4)2=4,
解得:x=2或x=4(舍),
即F(2,2),
令y=x2+x+4=2,解得:x=1+或x=1-(舍),
∴P(1+,2);
③若F为和谐点,
同理有:OF=DF,即F(1,3),
令y=x2+x+4=3,解得:x=1+或x=1-(舍),
即P(1+,3),
综上所述,点P的坐标为(1+,2),(1+,3).
3.(2019·三门峡二模)定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,﹣3),C(﹣1,﹣5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为( )
A.(1,﹣2) B.(2,﹣1) C.(,﹣1) D.(3,0)
【答案】A.
【解析】解:设M(x,y),由“实际距离”的定义可知:
点M(x,y)中,﹣1<x<5,﹣5<y<1,
∵M到A,B,C实际距离相等,
∴|x﹣3|+|y﹣1|=|x﹣5|+|y+3|=|x+1|+|y+5|,
A.(1,﹣2),将x=1,y=-2代入上式,满足要求,∴A符合要求;
验证B、C、D不符合要求,
故答案为:A.
4.(2019·开封模拟)【阅读理解】
截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD,连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是 ;
【拓展延伸】
(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;
【知识应用】
(3)如图3,两块斜边长都为14cm的三角板,把斜边重叠摆放在一起,则两块三角板的直角顶点之间的距离PQ的长分别为 cm.
图1 图2 图3
【答案】(1)DA=DC+DB;(2)见解析;(3).
【解析】解:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵∠BDC=120°,
∴∠ABD+∠ACD=180°,
∵∠ACE+∠ACD=180°,
∴∠ABD=∠ACE,
∴△ABD≌△ACE,
∴AD=AE,∠BAD=∠CAE,
∵∠ABC=60°,即∠BAD+∠DAC=60°,
∴∠DAC+∠CAE=60°,即∠DAE=60°,
∴△ADE是等边三角形,
∴DA=DE=DC+CE=DC+DB,
即DA=DC+DB,
(2)DA=DB+DC,
延长DC到点E,使CE=BD,连接AE,
与(1)中证法知,△ABD≌△ACE,
∴AD=AE,∠BAD=∠CAE,
∴∠DAE=∠BAC=90°,
∴DA2+AE2=DE2,
即2DA2=(DB+DC)2,
∴DA=DB+DC;
(3)连接PQ,
∵MN=14,∠QMN=30°,
∴QN=MN=7,
在Rt△MQN中,由勾股定理得:MQ=7,
由(2)知PQ=QN+QM
∴PQ=7+7,
∴PQ=.
5.(2019·郑州联考)如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明:
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸:
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
图1 图2
【答案】(1)PM=PN,PM⊥PN;(2)(3)见解析.
【解析】解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=BD,
同理:PM∥CE,PM=CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
同理,∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN
=∠DCA+∠ADC
=90°,
即PM⊥PN,
(2)△PMN是等腰直角三角形,理由如下:
由旋转性质得,∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∴∠ABD=∠ACE,BD=CE,
由三角形的中位线得,PM∥CE,PN∥BD,PN=BD,PM=CE,
∴PM=PN,∠DPM=∠DCE,∠PNC=∠DBC,
∴∠MPN=∠DPM+∠DPN
=∠DCE+∠DCB+∠DBC
=∠BCE+∠DBC
=∠ACB+∠ACE+∠DBC
=∠ACB+∠ABD+∠DBC
=∠ACB+∠ABC,
∵∠BAC=90°,
∴∠ACB+∠ABC=90°,
∴∠MPN=90°,
即△PMN是等腰直角三角形;
(3)由(2)知,△PMN是等腰直角三角形,PM=PN=BD,
∴当PM最大时(即BD最大时),△PMN面积最大,
当点D在BA延长线上时,BD最大,最大为:14,
此时,PM=7,
∴△PMN面积的最大值为:PM2=.
6.(2019·平顶山三模)已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β,
(1)如图1,若点D在线段BC上,点E在线段AC上.∠ABC=60°,∠ADE=70°,则α= °;β= °.
(2)如图2,若点D在线段BC上,点E在线段AC上,则α,β之间有什么关系式?说明理由.
(3)是否存在不同于(2)中的α,β之间的关系式?若存在,请写出这个关系式(写出一种即可),说明理由;若不存在,请说明理由.
图1 图2
【答案】(1)20,10;(2)(3)见解析.
【解析】解:(1)∵AB=AC,∠ABC=60°,
∴∠BAC=60°,
∵AD=AE,∠ADE=70°,
∴∠DAE=180°﹣2∠ADE=40°,
∴α=∠BAD=20°,
∴∠ADC=α+∠ABD=80°,
∴β=∠ADC﹣∠ADE=10°,
故答案为:20,10;
(2)∠ADC=α+∠B,
∠ADC=∠ADE+β
=∠AED+β
=β+∠C+β,
∴α+∠B=β+∠C+β,
∵∠B=∠C,
∴α=2β;
(3)存在;
①当点E在CA的延长线上,点D在线段BC上,
可得:α=2β﹣180°;
②当点E在CA的延长线上,点D在CB的延长线上,
可得α=180°﹣2β.
7.(2019·郑州外国语模拟)如图,在平面直角坐标系xOy中,直线y=kx+k与双曲线(x>0)交于点A(1,a).
(1)求a,k的值;
(2)已知直线l过点D(2,0)且平行于直线y=kx+k,点P(m,n),(m>3)是直线l上一动点,过点P作坐标轴的平行线,交双曲线于点M、N,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为W. 横、纵坐标都是整数的点叫做整点.
①当m=4时,直接写出区域W内的整点个数;
②若区域W内的整点个数正好是8个,结合图象,求m的取值范围.
【答案】见解析.
【解析】解:(1)∵点A(1,a)在双曲线上,
∴a=4.
∴点A的坐标为(1,4).
将A(1,4)代入y=kx+k,得k=2;
(2)①区域W内整点个数是3;
∵直线l过点D(2,0)且平行于直线y=2x+2,
∴直线l的解析式为y=2x-4.
当m=4时,n=2m-4=4,点P的坐标为(4,4).
画出图象,观察图形,可知区域W内的整点个数是3.
②
当2x-4=5时,x=4.5,此时区域W内有8个整点;
结合函数图象,若区域W内的整点个数为8个,则m的取值范围为3<m≤4.5.
8.(2019·郑州外国语模拟)如图,一段抛物线y=-x2+4(-2≤x≤2)为C1,与x轴交于A0、A1两点,顶点为D1;将C1绕点A1选择180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t= x1+x2+x3,则t的取值范围是( )
A. 6【答案】D.
【解析】解:旋转后的抛物线的解析式为:y=(x﹣4)2﹣4,
∵设x1,x2,x3均为正数,
∴点P1(x1,y1),P2(x2,y2)在第四象限,
由对称性可知:x1+x2=8,
∵2≤x3≤4,
∴10≤x1+x2+x3≤12,即10≤t≤12,
故答案为:D.
9.(2019·南阳二模)如图,在 8×8 的网格中,每个小方格都是边长为 1 的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于 y 轴的抛物线与网格对角线 OM 的两个交点为 A,B,其顶点为 C,如果△ABC 是该抛物线的内接格点三角形,且 AB=,点 A,B,C 的横坐标 xA,xB,xC 满足 xA<xC<xB,那么符合上述条件的抛物线的条数是 .
【答案】10.
【解析】解:若抛物线开口朝下,当A(0,0)时,由AB=得:B(3,3),此时C(2,4),抛物线的解析式为:y=-x2+4x,
该函数图象每向右平移1个单位,向上平移1个单位可得到一条抛物线,可平移4次,即有5条抛物线;
同理,开口朝上的抛物线有5条,
综上所述,共有10条抛物线符合要求.
10.(2017?禹州市二模)有这样一个问题:探究函数y=x2+的图象与性质,小东根据学习函数的经验,对函数y=x2+的图象与性质进行了探究,下面是小东的探究过程,请补充完整:
(1)下表是y与x的几组对应值.
x
…
﹣3
﹣2
﹣1
1
2
3
…
y
…
m
…
函数y=x2+的自变量x的取值范围是 ,m的值为 ;
(2)在如图所示的平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并画出该函数的大致图象;
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程x2+=0有 个实数根;
②方程x2+=2有 个实数根;
③结合函数的图象,写出该函数的一条性质 .
【答案】(1)x≠0,;(2)见解析.(3)1;1;3;函数没有最大值;这个函数没有最小值;函数图象不经过第四象限;当x<0时,y随x的增大而减小.
【解析】解:(1)由题意:x≠0,m=.
(2)函数图象如图所示.
(3)①由图象可知与x轴有一个交点,方程x2+=0有一个实数根.
故答案为:1,1.
②观察图象可知,方程x2+=2有3个实数根,
故答案为:3.
③函数性质:函数没有最大值;函数没有最小值;函数图象不经过第四象限等,答案不唯一.
【例1】(2019·开封模拟)参照学习函数的过程与方法,探究函数(x≠0)的图象与性质.
因为,即,所以我们对比函数来探究.
列表:
x
…
-4
-3
-2
-1
1
2
3
4
…
…
1
2
4
-4
-2
-1
…
…
2
3
5
-3
-1
0
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来.
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而__________;(填“增大”或“减小”)
②的图象是由的图象向_______平移______个单位而得到;
③图象关于点__________中心对称.(填点的坐标)
(3)函数与直线y=-2x+1交于点A,B,求△AOB的面积.
【变式1-1】(2019·郑州模拟)探究函数的图象与性质
(1)函数的自变量x的取值范围是 ;
(2)下列四个函数图象中可能是函数的图象的是
(3)对于函数,当x>0时,求y的取值范围.
解:∵x>0,
∴==+ ,
∵≥0,
∴y≥ .
拓展运用
(4)若函数,则y的取值范围是 .
【例2】(2018·洛阳三模)在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”. 有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
已知抛物线与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,点A的坐标为 ,点B的标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
【变式2-1】(2019·安阳一模)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线系数”.
(1)任意抛物线都有“抛物线三角形”是 (填“真”或“假”)命题;
(2)若一条抛物线系数为[1,0,﹣2],则其“抛物线三角形”的面积为 ;
(3)若一条抛物线系数为[﹣1,2b,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;
(4)在(3)的前提下,该抛物线的顶点为A,与x轴交于O,B两点,在抛物线上是否存在一点P,过P作PQ⊥x轴于点Q,使得△BPQ∽△OAB?如果存在,求出P点坐标;如果不存在,请说明理由.
强化精炼:
1.(2018·逆袭卷)有这样一个问题:探究函数的图象与性质.
下面是小强的探究过程,请补充完整:
(1)函数的自变量x的取值范围 ;
(2)下表是y与x的几组对应值.
x
…
-5
-4
-3
-2
0
1
2
3
…
y
…
-2
0
…
如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.
①观察图中各点的位置发现:点A1和B1,点A2和B2,A3和B3,A4和B4均关于某点中心对称,则该点的坐标为 ;
②小文分析函数的表达式发现:当x<-1时,函数的最大值为-2,则该函数图象在直线x=-1左侧的最高点的坐标为
(3)画出该函数的图象,并写出该函数的一条性质
2.(2019·偃师一模)如图,抛物线y=ax2+bx+4(a≠0)交x轴于点A(4,0),B(-2,0),交y轴于点C.
(1)求抛物线的解析式.
(2)点 Q 是 x 轴上位于点A,B之间的一个动点,点E为线段BC上一个动点,若始终保持∠EQB=∠CAB,连接CQ,设△CQE 的面积为S,点Q的横坐标为m,求出S关于m的函数关系式,并求出当S取最大值时点Q的坐标.
(3)点 P 为抛物线上位于 AC 上方的一个动点,过点 P 作 PF⊥y 轴,交直线 AC 于点 F,点 D 的坐标为(2,0),若 O,D,F 三点中,当其中一点恰好 位于另外两点的垂直平分线上时,我们把这个点叫做另外两点的“和谐点”,请判断这三点是否有“和谐点”的存在,若存在,请直接写出此时点P的坐标;若不存在,请说明理由.
3.(2019·三门峡二模)定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,﹣3),C(﹣1,﹣5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为( )
A.(1,﹣2) B.(2,﹣1) C.(,﹣1) D.(3,0)
4.(2019·开封模拟)【阅读理解】
截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD,连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是 ;
【拓展延伸】
(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;
【知识应用】
(3)如图3,两块斜边长都为14cm的三角板,把斜边重叠摆放在一起,则两块三角板的直角顶点之间的距离PQ的长分别为 cm.
图1 图2 图3
5.(2019·郑州联考)如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明:
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸:
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
图1 图2
6.(2019·平顶山三模)已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β,
(1)如图1,若点D在线段BC上,点E在线段AC上.∠ABC=60°,∠ADE=70°,则α= °;β= °.
(2)如图2,若点D在线段BC上,点E在线段AC上,则α,β之间有什么关系式?说明理由.
(3)是否存在不同于(2)中的α,β之间的关系式?若存在,请写出这个关系式(写出一种即可),说明理由;若不存在,请说明理由.
图1 图2
7.(2019·郑州外国语模拟)如图,在平面直角坐标系xOy中,直线y=kx+k与双曲线(x>0)交于点A(1,a).
(1)求a,k的值;
(2)已知直线l过点D(2,0)且平行于直线y=kx+k,点P(m,n),(m>3)是直线l上一动点,过点P作坐标轴的平行线,交双曲线于点M、N,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为W. 横、纵坐标都是整数的点叫做整点.
①当m=4时,直接写出区域W内的整点个数;
②若区域W内的整点个数正好是8个,结合图象,求m的取值范围.
8.(2019·郑州外国语模拟)如图,一段抛物线y=-x2+4(-2≤x≤2)为C1,与x轴交于A0、A1两点,顶点为D1;将C1绕点A1选择180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t= x1+x2+x3,则t的取值范围是( )
A. 6
10.(2017?禹州市二模)有这样一个问题:探究函数y=x2+的图象与性质,小东根据学习函数的经验,对函数y=x2+的图象与性质进行了探究,下面是小东的探究过程,请补充完整:
(1)下表是y与x的几组对应值.
x
…
﹣3
﹣2
﹣1
1
2
3
…
y
…
m
…
函数y=x2+的自变量x的取值范围是 ,m的值为 ;
(2)在如图所示的平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并画出该函数的大致图象;
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程x2+=0有 个实数根;
②方程x2+=2有 个实数根;
③结合函数的图象,写出该函数的一条性质 .
2020年中考数学三轮易错复习:专题18 利用函数图象研究函数性质及新题型
【例1】(2019·开封模拟)参照学习函数的过程与方法,探究函数(x≠0)的图象与性质.
因为,即,所以我们对比函数来探究.
列表:
x
…
-4
-3
-2
-1
1
2
3
4
…
…
1
2
4
-4
-2
-1
…
…
2
3
5
-3
-1
0
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来.
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而__________;(填“增大”或“减小”)
②的图象是由的图象向_______平移______个单位而得到;
③图象关于点__________中心对称.(填点的坐标)
(3)函数与直线y=-2x+1交于点A,B,求△AOB的面积.
【答案】(1)见解析;(2)增大;上,1;(0,1);(3)见解析.
【解析】解:(1)如图所示;
(2)①增大;②上,1;③(0,1);
(3)联立:与直线y=-2x+1,
解得:x=1,y=-1或x=-1,y=3,
∴S△AOB=×2×4-×1×4-×2×1=1.
【变式1-1】(2019·郑州模拟)探究函数的图象与性质
(1)函数的自变量x的取值范围是 ;
(2)下列四个函数图象中可能是函数的图象的是
(3)对于函数,当x>0时,求y的取值范围.
解:∵x>0,
∴==+ ,
∵≥0,
∴y≥ .
拓展运用
(4)若函数,则y的取值范围是 .
【答案】(1)x≠0;(2)C;(3)4,4;(4)y≥1或y≤-11.
【解析】解:(1)由分式的意义,知x≠0;
(2)∵x≠0,
∴A错误;
当x>0时,y>0,故B、D错误,
∴选项C正确;
(3)4;4;
(4)当x>0时,==
∵≥0,
∴y≥1;
当x<0时,
=
=,
∵≤0
∴y≤-11;
综上所述,y≥1或y≤-11.
【例2】(2018·洛阳三模)在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”. 有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
已知抛物线与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,点A的坐标为 ,点B的标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
【答案】(1),(-2,),(1,0);(2)(3)见解析.
【解析】解:(1)抛物线,由定义知:
其梦想直线的解析式为:,
联立,,解得:
或,
故答案为:,(-2,),(1,0).
(2)由题意知C(-3,0),过A作AG⊥y轴于G,
①当点N在y轴上时,△AMN是梦想三角形,
AC=AN=,
由抛物线的对称轴x=-1,A(-2,),得:AG=2,G(0,),
在Rt△ANG中,由勾股定理得:
GN=3,
∴N(0,+3)或(0,-3),
当ON=+3时,则MN>OG>CM,与MN=CM矛盾,不合题意,
∴N(0,-3),
②当点M在y轴上时,△AMN为梦想三角形,
即M点在坐标原点,M(0,0),
在Rt△AGM中, AG=2,GM=,tan∠AMG=,
∴∠AMG=30°,
∴∠AMC=∠AMN=∠NMB=60°,
过点N作NP⊥x轴,
在Rt△NMP中,MN=CM=3,
∴NP=,OP=,即N(,),
综上所述,点N的坐标为(0,-3),(,).
(3)设E(-1,m),F(n,),
∵A(-2,),C(-3,0),
①当四边形ACEF是平行四边形时,有:
,
解得:,
即E(-1,),F(0,);
②当四边形AECF是平行四边形时,有:
,
解得:,
即E(-1,),F(-4,);
③当四边形AEFC是平行四边形时,有:
,
解得:,
此时F与A重合,不符题意,舍去;
综上所述,E(-1,),F(-4,)或E(-1,),F(0,).
【变式2-1】(2019·安阳一模)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线系数”.
(1)任意抛物线都有“抛物线三角形”是 (填“真”或“假”)命题;
(2)若一条抛物线系数为[1,0,﹣2],则其“抛物线三角形”的面积为 ;
(3)若一条抛物线系数为[﹣1,2b,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;
(4)在(3)的前提下,该抛物线的顶点为A,与x轴交于O,B两点,在抛物线上是否存在一点P,过P作PQ⊥x轴于点Q,使得△BPQ∽△OAB?如果存在,求出P点坐标;如果不存在,请说明理由.
【答案】(1)假;(2);(3)(4)见解析.
【解析】解:(1)∵抛物线与x轴的交点个数有三种情况:没交点,一个交点,两个交点,
∴任意抛物线都有“抛物线三角形”是假命题,
故答案为:假;
(2)∵一条抛物线系数为[1,0,﹣2],
∴a=1,b=0,c=﹣2,
∴抛物线解析式为y=x2﹣2,
当x=0,y=﹣2,
当y=0,解得,x=,
∴“抛物线三角形”的面积为×(+)×2=2
故答案为:2.
(3)由题意得:抛物线解析式为:y=﹣x2+2bx,
与x轴交点为:(0,0),(2b,0);
若“抛物线三角形”是个直角三角形,则是等腰直角三角形,
∴顶点为(b,b)或(b,﹣b),
①当顶点为(b,b)时,
有:b=﹣b2+2b2,
解得b=0(舍去)或b=1
∴y=﹣x2+2x,
②当顶点为(b,﹣b)时,
有:﹣b=﹣b2+2b2,
解得b=0(舍去)或b=﹣1
∴y=﹣x2﹣2x,
(4)∵△AOB为等腰直角三角形,且△BPQ∽△OAB,
∴△BPQ为等腰直角三角形,
①y=﹣x2+2x,
设P(a,﹣a2+2a),
则Q(a,0)
则|﹣a2+2a|=|2﹣a|,
解得:a=1(舍)或a=2(舍去)或a=-1,
∴P(﹣1,﹣3);
②y=﹣x2﹣2x,
同理得:P(1,3);
综上所述,点P(﹣1,﹣3)或(1,3).
强化精炼:
1.(2018·逆袭卷)有这样一个问题:探究函数的图象与性质.
下面是小强的探究过程,请补充完整:
(1)函数的自变量x的取值范围 ;
(2)下表是y与x的几组对应值.
x
…
-5
-4
-3
-2
0
1
2
3
…
y
…
-2
0
…
如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.
①观察图中各点的位置发现:点A1和B1,点A2和B2,A3和B3,A4和B4均关于某点中心对称,则该点的坐标为 ;
②小文分析函数的表达式发现:当x<-1时,函数的最大值为-2,则该函数图象在直线x=-1左侧的最高点的坐标为
(3)画出该函数的图象,并写出该函数的一条性质
【答案】(1)x≠-1;(2)①(-1,-1);②(-2,-2);(3)见解析.
【解析】解:(1)由2x+2≠0得,x≠-1;
(2)①由图象知,该点坐标为:(-1,-1);
②当x=-2时,y=-2,∴图象在直线x=-1左侧的最高点的坐标为(-2,-2);
③图象见下图.
函数性质:函数图象不经过第四象限;当x<-2时,y随x的增大而增大;当-2
(1)求抛物线的解析式.
(2)点 Q 是 x 轴上位于点A,B之间的一个动点,点E为线段BC上一个动点,若始终保持∠EQB=∠CAB,连接CQ,设△CQE 的面积为S,点Q的横坐标为m,求出S关于m的函数关系式,并求出当S取最大值时点Q的坐标.
(3)点 P 为抛物线上位于 AC 上方的一个动点,过点 P 作 PF⊥y 轴,交直线 AC 于点 F,点 D 的坐标为(2,0),若 O,D,F 三点中,当其中一点恰好 位于另外两点的垂直平分线上时,我们把这个点叫做另外两点的“和谐点”,请判断这三点是否有“和谐点”的存在,若存在,请直接写出此时点P的坐标;若不存在,请说明理由.
【答案】见解析.
【解析】解:(1)∵y=ax2+bx+4交x轴于点A(4,0),B(-2,0),
∴,
解得:a=,b=1,
∴抛物线的解析式为:y=x2+x+4.
(2)y=x2+x+4与y轴交于点C,
∴C(0,4),
∵A(4,0),B(-2,0),
设直线AC的解析式为:y=kx+n,
∴4k+n=0,n=4,
解得:k=-1,n=4,
即直线AC的解析式:y=-x+4,
同理得:直线BC的解析式为:y=2x+4,
∵∠EQB=∠CAB,
∴EQ∥AC,
∵点Q的坐标为(m,0),
设直线EQ解析式为:y=-x+m,
联立:y=-x+m,y=2x+4解得:
x=,y=,
即E(,),
设直线EQ交y轴于点H,
如下图所示,
∴S=·CH·|xE-xQ|
=,其中:-2
∴当m=1时,S取最大值,此时Q点坐标为(1,0).
(3)存在,理由如下,如下图所示,
和谐点为O(0,0),D(2,0),设F(x,-x+4),
①若O是和谐点,
则OF=OD=2,
即:OF2=OD2=4,
x2+(-x+4)2=4,此方程无实数解,即O不是和谐点;
②若D是和谐点,
同理:OD=DF=2,
即:(2-x)2+(-x+4)2=4,
解得:x=2或x=4(舍),
即F(2,2),
令y=x2+x+4=2,解得:x=1+或x=1-(舍),
∴P(1+,2);
③若F为和谐点,
同理有:OF=DF,即F(1,3),
令y=x2+x+4=3,解得:x=1+或x=1-(舍),
即P(1+,3),
综上所述,点P的坐标为(1+,2),(1+,3).
3.(2019·三门峡二模)定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,﹣3),C(﹣1,﹣5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为( )
A.(1,﹣2) B.(2,﹣1) C.(,﹣1) D.(3,0)
【答案】A.
【解析】解:设M(x,y),由“实际距离”的定义可知:
点M(x,y)中,﹣1<x<5,﹣5<y<1,
∵M到A,B,C实际距离相等,
∴|x﹣3|+|y﹣1|=|x﹣5|+|y+3|=|x+1|+|y+5|,
A.(1,﹣2),将x=1,y=-2代入上式,满足要求,∴A符合要求;
验证B、C、D不符合要求,
故答案为:A.
4.(2019·开封模拟)【阅读理解】
截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD,连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是 ;
【拓展延伸】
(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;
【知识应用】
(3)如图3,两块斜边长都为14cm的三角板,把斜边重叠摆放在一起,则两块三角板的直角顶点之间的距离PQ的长分别为 cm.
图1 图2 图3
【答案】(1)DA=DC+DB;(2)见解析;(3).
【解析】解:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵∠BDC=120°,
∴∠ABD+∠ACD=180°,
∵∠ACE+∠ACD=180°,
∴∠ABD=∠ACE,
∴△ABD≌△ACE,
∴AD=AE,∠BAD=∠CAE,
∵∠ABC=60°,即∠BAD+∠DAC=60°,
∴∠DAC+∠CAE=60°,即∠DAE=60°,
∴△ADE是等边三角形,
∴DA=DE=DC+CE=DC+DB,
即DA=DC+DB,
(2)DA=DB+DC,
延长DC到点E,使CE=BD,连接AE,
与(1)中证法知,△ABD≌△ACE,
∴AD=AE,∠BAD=∠CAE,
∴∠DAE=∠BAC=90°,
∴DA2+AE2=DE2,
即2DA2=(DB+DC)2,
∴DA=DB+DC;
(3)连接PQ,
∵MN=14,∠QMN=30°,
∴QN=MN=7,
在Rt△MQN中,由勾股定理得:MQ=7,
由(2)知PQ=QN+QM
∴PQ=7+7,
∴PQ=.
5.(2019·郑州联考)如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明:
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸:
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
图1 图2
【答案】(1)PM=PN,PM⊥PN;(2)(3)见解析.
【解析】解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=BD,
同理:PM∥CE,PM=CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
同理,∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN
=∠DCA+∠ADC
=90°,
即PM⊥PN,
(2)△PMN是等腰直角三角形,理由如下:
由旋转性质得,∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∴∠ABD=∠ACE,BD=CE,
由三角形的中位线得,PM∥CE,PN∥BD,PN=BD,PM=CE,
∴PM=PN,∠DPM=∠DCE,∠PNC=∠DBC,
∴∠MPN=∠DPM+∠DPN
=∠DCE+∠DCB+∠DBC
=∠BCE+∠DBC
=∠ACB+∠ACE+∠DBC
=∠ACB+∠ABD+∠DBC
=∠ACB+∠ABC,
∵∠BAC=90°,
∴∠ACB+∠ABC=90°,
∴∠MPN=90°,
即△PMN是等腰直角三角形;
(3)由(2)知,△PMN是等腰直角三角形,PM=PN=BD,
∴当PM最大时(即BD最大时),△PMN面积最大,
当点D在BA延长线上时,BD最大,最大为:14,
此时,PM=7,
∴△PMN面积的最大值为:PM2=.
6.(2019·平顶山三模)已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β,
(1)如图1,若点D在线段BC上,点E在线段AC上.∠ABC=60°,∠ADE=70°,则α= °;β= °.
(2)如图2,若点D在线段BC上,点E在线段AC上,则α,β之间有什么关系式?说明理由.
(3)是否存在不同于(2)中的α,β之间的关系式?若存在,请写出这个关系式(写出一种即可),说明理由;若不存在,请说明理由.
图1 图2
【答案】(1)20,10;(2)(3)见解析.
【解析】解:(1)∵AB=AC,∠ABC=60°,
∴∠BAC=60°,
∵AD=AE,∠ADE=70°,
∴∠DAE=180°﹣2∠ADE=40°,
∴α=∠BAD=20°,
∴∠ADC=α+∠ABD=80°,
∴β=∠ADC﹣∠ADE=10°,
故答案为:20,10;
(2)∠ADC=α+∠B,
∠ADC=∠ADE+β
=∠AED+β
=β+∠C+β,
∴α+∠B=β+∠C+β,
∵∠B=∠C,
∴α=2β;
(3)存在;
①当点E在CA的延长线上,点D在线段BC上,
可得:α=2β﹣180°;
②当点E在CA的延长线上,点D在CB的延长线上,
可得α=180°﹣2β.
7.(2019·郑州外国语模拟)如图,在平面直角坐标系xOy中,直线y=kx+k与双曲线(x>0)交于点A(1,a).
(1)求a,k的值;
(2)已知直线l过点D(2,0)且平行于直线y=kx+k,点P(m,n),(m>3)是直线l上一动点,过点P作坐标轴的平行线,交双曲线于点M、N,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为W. 横、纵坐标都是整数的点叫做整点.
①当m=4时,直接写出区域W内的整点个数;
②若区域W内的整点个数正好是8个,结合图象,求m的取值范围.
【答案】见解析.
【解析】解:(1)∵点A(1,a)在双曲线上,
∴a=4.
∴点A的坐标为(1,4).
将A(1,4)代入y=kx+k,得k=2;
(2)①区域W内整点个数是3;
∵直线l过点D(2,0)且平行于直线y=2x+2,
∴直线l的解析式为y=2x-4.
当m=4时,n=2m-4=4,点P的坐标为(4,4).
画出图象,观察图形,可知区域W内的整点个数是3.
②
当2x-4=5时,x=4.5,此时区域W内有8个整点;
结合函数图象,若区域W内的整点个数为8个,则m的取值范围为3<m≤4.5.
8.(2019·郑州外国语模拟)如图,一段抛物线y=-x2+4(-2≤x≤2)为C1,与x轴交于A0、A1两点,顶点为D1;将C1绕点A1选择180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t= x1+x2+x3,则t的取值范围是( )
A. 6
【解析】解:旋转后的抛物线的解析式为:y=(x﹣4)2﹣4,
∵设x1,x2,x3均为正数,
∴点P1(x1,y1),P2(x2,y2)在第四象限,
由对称性可知:x1+x2=8,
∵2≤x3≤4,
∴10≤x1+x2+x3≤12,即10≤t≤12,
故答案为:D.
9.(2019·南阳二模)如图,在 8×8 的网格中,每个小方格都是边长为 1 的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于 y 轴的抛物线与网格对角线 OM 的两个交点为 A,B,其顶点为 C,如果△ABC 是该抛物线的内接格点三角形,且 AB=,点 A,B,C 的横坐标 xA,xB,xC 满足 xA<xC<xB,那么符合上述条件的抛物线的条数是 .
【答案】10.
【解析】解:若抛物线开口朝下,当A(0,0)时,由AB=得:B(3,3),此时C(2,4),抛物线的解析式为:y=-x2+4x,
该函数图象每向右平移1个单位,向上平移1个单位可得到一条抛物线,可平移4次,即有5条抛物线;
同理,开口朝上的抛物线有5条,
综上所述,共有10条抛物线符合要求.
10.(2017?禹州市二模)有这样一个问题:探究函数y=x2+的图象与性质,小东根据学习函数的经验,对函数y=x2+的图象与性质进行了探究,下面是小东的探究过程,请补充完整:
(1)下表是y与x的几组对应值.
x
…
﹣3
﹣2
﹣1
1
2
3
…
y
…
m
…
函数y=x2+的自变量x的取值范围是 ,m的值为 ;
(2)在如图所示的平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并画出该函数的大致图象;
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程x2+=0有 个实数根;
②方程x2+=2有 个实数根;
③结合函数的图象,写出该函数的一条性质 .
【答案】(1)x≠0,;(2)见解析.(3)1;1;3;函数没有最大值;这个函数没有最小值;函数图象不经过第四象限;当x<0时,y随x的增大而减小.
【解析】解:(1)由题意:x≠0,m=.
(2)函数图象如图所示.
(3)①由图象可知与x轴有一个交点,方程x2+=0有一个实数根.
故答案为:1,1.
②观察图象可知,方程x2+=2有3个实数根,
故答案为:3.
③函数性质:函数没有最大值;函数没有最小值;函数图象不经过第四象限等,答案不唯一.
同课章节目录
