6.4.5 正弦定理(一)课件 (共32张PPT)
文档属性
| 名称 | 6.4.5 正弦定理(一)课件 (共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 372.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 00:00:00 | ||
图片预览






文档简介
课件32张PPT。高一数学6.4.5 正弦定理(一) 1.问题的引入:
.(1)在我国古代就有嫦娥奔月的神话故事.明月
高悬,我们仰望夜空,会有无限遐想,不禁会问,
月亮离我们地球有多远呢?科学家们是怎样
测出来的呢?(2)设A,B两点在河的两岸, 只给你米尺和量角设备,不过河你可以测出它们之间的距离吗?AB我们这一节所学习的内容就是解决这些问题
的有力工具.知识回顾1.已知三角形的某些边和角,求其他的边 和角的过程叫做解三角形.3.余弦定理解三角形
1、已知两边及其夹角,求第三边和其他两个角
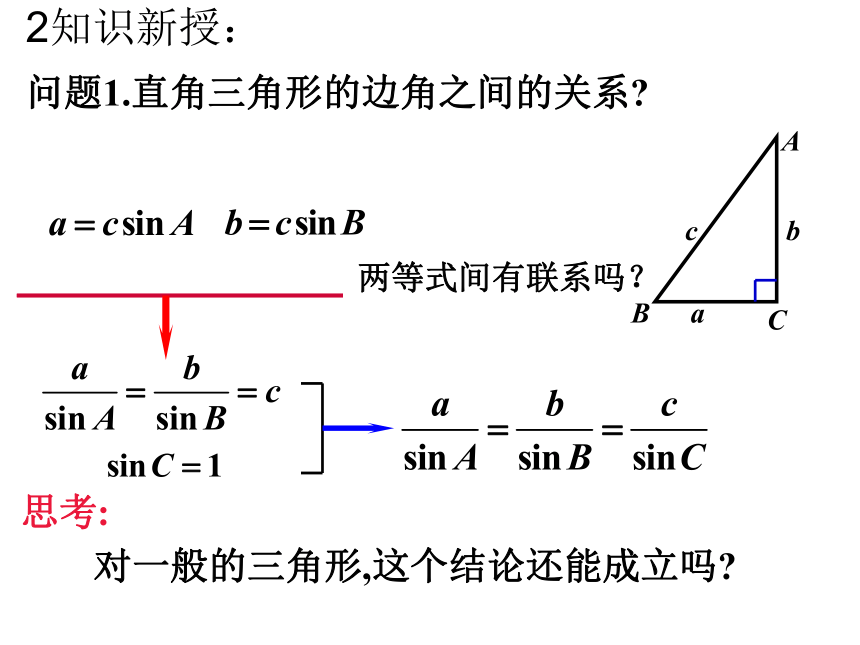
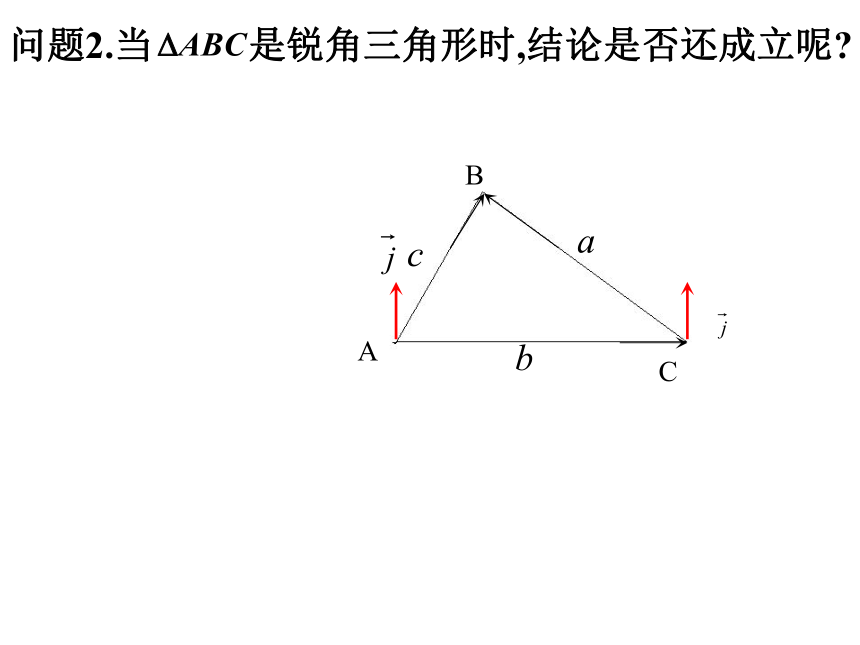
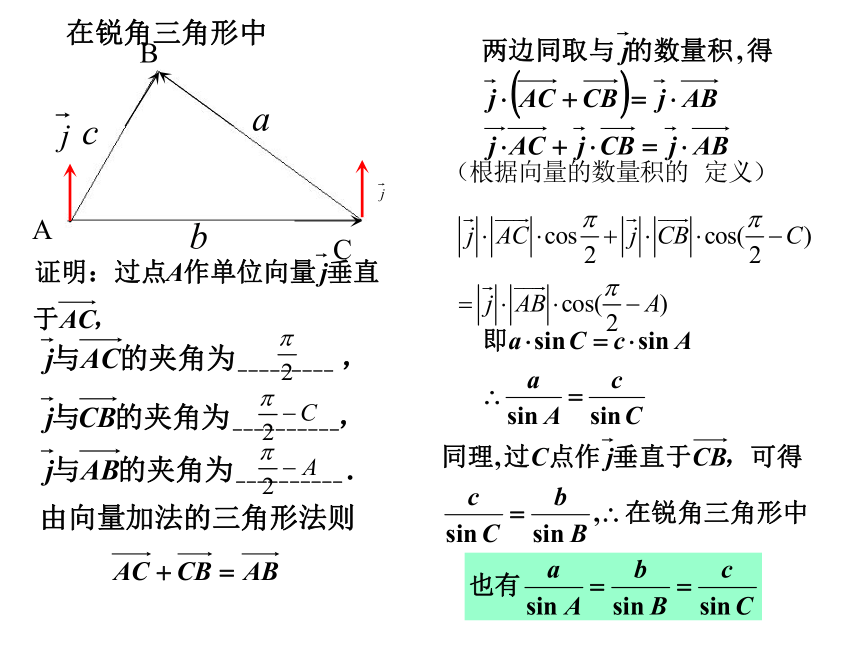
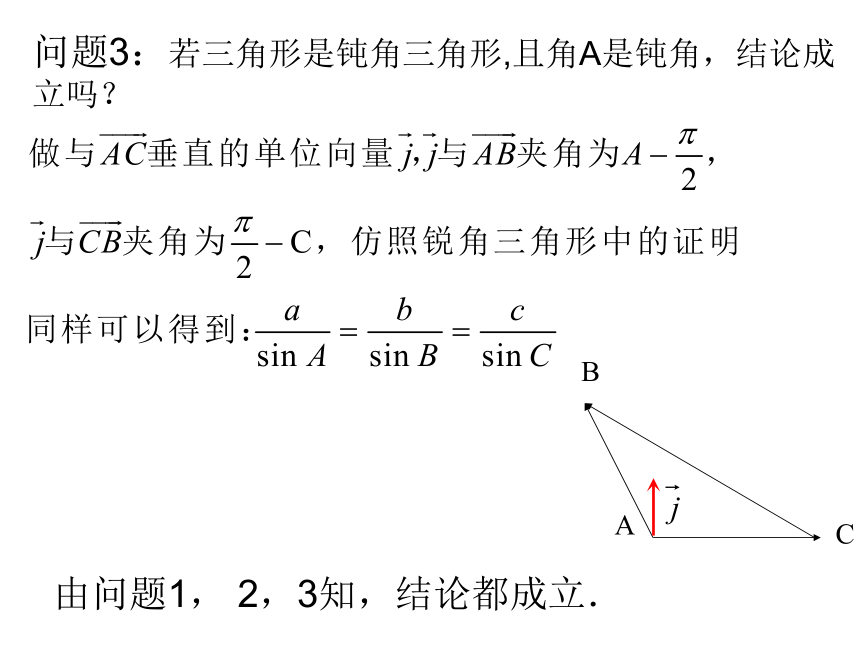
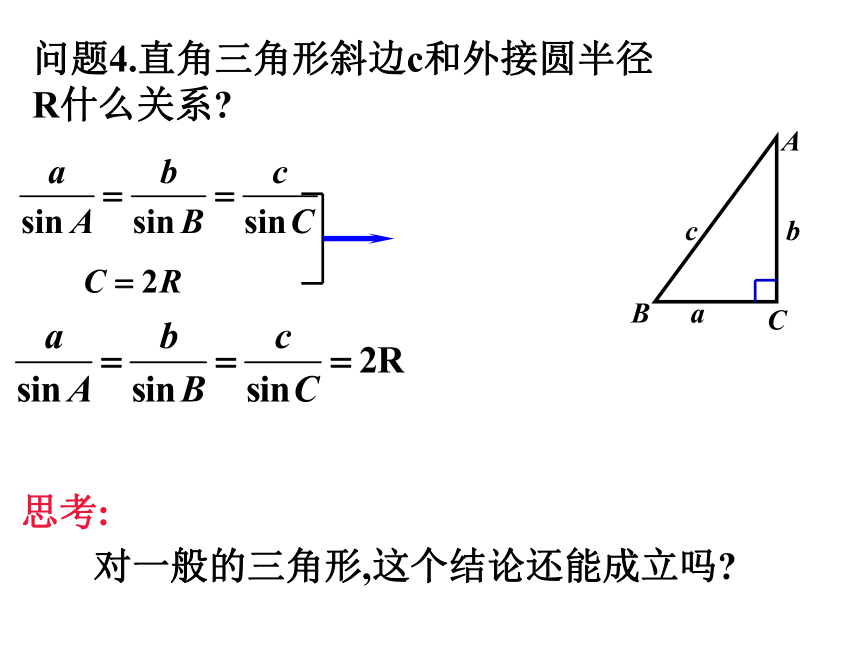
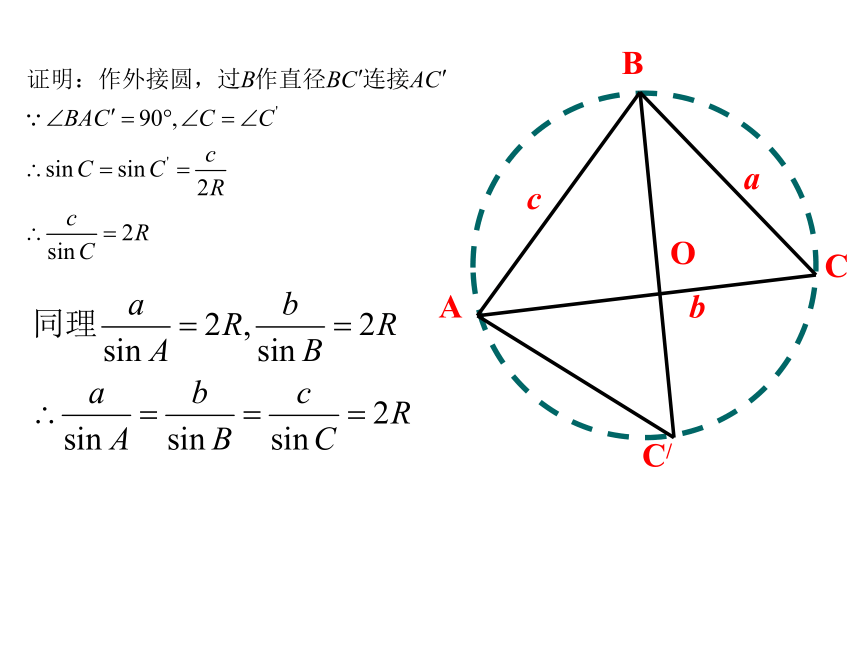
2、已知三边求三个角;问题1.直角三角形的边角之间的关系? 两等式间有联系吗?思考:对一般的三角形,这个结论还能成立吗?2知识新授:问题2.当 是锐角三角形时,结论是否还成立呢?BAC在锐角三角形中由向量加法的三角形法则由问题1, 2,3知,结论都成立.问题3:若三角形是钝角三角形,且角A是钝角,结论成 立吗?(1)文字叙述正弦定理:在一个三角形中,各边和它所对角 的正弦的比相等.(2)结构特点表达形式统一对称,结果和谐优美.正弦定理:问题4.直角三角形斜边c和外接圆半径R什么关系? 思考:对一般的三角形,这个结论还能成立吗?3.定理的应用(1)已知三角形的两个内角和一边,利用正弦定理解三角形1.在△ABC中,已知 A=75°,B= 45°,c=
求a , b.2.在△ABC中,已知 A=30°,B=120°,b=12
求a , c.练习你学会了吗?课后思考:你还会用其他方法证明正弦定理吗?作业:课本P48 1(1)2(2)3 P52 7 (1)高一数学6.4.5 正弦定理(二)知识回顾:
正弦定理正弦定理应用
(2)已知三角形两边和其中一边的对角,解三角形思考:本题为什么会有两个解?练习2(1) 已知a=16,b= ,A=30° 解三角形解:由正弦定理所以B=60°,或B=120°C=90°C=30°当B=120°时在例 2 中,将已知条件改为以下几种情况,不解三角形判断有几组解? (3) c=2,B=30°,b=0.8.(1) c=2,B=30°,b=1 ;(2) c=2,B=30°,b= 3; 思考:正弦定理应用3:不解三角形判断三角形解的个数(1)一解(2)一解(3)无解一解一解无解练习3:ABabCABabCABabCab 一解思考:若角A为钝角或直角,三角形解的情况又如何?ab无解一解两解一解无解一解条件图形总结(1)当 是锐角三角形时,D如图:作AB上的高是CD,根椐
三角形的定义,得到应用4:三角形的面积公式E(2)当 是钝角或直角三角形时,以上等式
是否仍然成立?思考:D结论:上述式子仍然成立;证明留给同学们自己探索 (1) 已知两边和其中一边的对角,可以求出三角形的其他的边和角。(此时可能有一解、二解、无解)
(2)不解三角形判断三角形解的个数
你学会了吗?作业:1.课本P54. 16,18,20,22谢谢
.(1)在我国古代就有嫦娥奔月的神话故事.明月
高悬,我们仰望夜空,会有无限遐想,不禁会问,
月亮离我们地球有多远呢?科学家们是怎样
测出来的呢?(2)设A,B两点在河的两岸, 只给你米尺和量角设备,不过河你可以测出它们之间的距离吗?AB我们这一节所学习的内容就是解决这些问题
的有力工具.知识回顾1.已知三角形的某些边和角,求其他的边 和角的过程叫做解三角形.3.余弦定理解三角形
1、已知两边及其夹角,求第三边和其他两个角
2、已知三边求三个角;问题1.直角三角形的边角之间的关系? 两等式间有联系吗?思考:对一般的三角形,这个结论还能成立吗?2知识新授:问题2.当 是锐角三角形时,结论是否还成立呢?BAC在锐角三角形中由向量加法的三角形法则由问题1, 2,3知,结论都成立.问题3:若三角形是钝角三角形,且角A是钝角,结论成 立吗?(1)文字叙述正弦定理:在一个三角形中,各边和它所对角 的正弦的比相等.(2)结构特点表达形式统一对称,结果和谐优美.正弦定理:问题4.直角三角形斜边c和外接圆半径R什么关系? 思考:对一般的三角形,这个结论还能成立吗?3.定理的应用(1)已知三角形的两个内角和一边,利用正弦定理解三角形1.在△ABC中,已知 A=75°,B= 45°,c=
求a , b.2.在△ABC中,已知 A=30°,B=120°,b=12
求a , c.练习你学会了吗?课后思考:你还会用其他方法证明正弦定理吗?作业:课本P48 1(1)2(2)3 P52 7 (1)高一数学6.4.5 正弦定理(二)知识回顾:
正弦定理正弦定理应用
(2)已知三角形两边和其中一边的对角,解三角形思考:本题为什么会有两个解?练习2(1) 已知a=16,b= ,A=30° 解三角形解:由正弦定理所以B=60°,或B=120°C=90°C=30°当B=120°时在例 2 中,将已知条件改为以下几种情况,不解三角形判断有几组解? (3) c=2,B=30°,b=0.8.(1) c=2,B=30°,b=1 ;(2) c=2,B=30°,b= 3; 思考:正弦定理应用3:不解三角形判断三角形解的个数(1)一解(2)一解(3)无解一解一解无解练习3:ABabCABabCABabCab 一解思考:若角A为钝角或直角,三角形解的情况又如何?a
三角形的定义,得到应用4:三角形的面积公式E(2)当 是钝角或直角三角形时,以上等式
是否仍然成立?思考:D结论:上述式子仍然成立;证明留给同学们自己探索 (1) 已知两边和其中一边的对角,可以求出三角形的其他的边和角。(此时可能有一解、二解、无解)
(2)不解三角形判断三角形解的个数
你学会了吗?作业:1.课本P54. 16,18,20,22谢谢
