2.2.1用样本的频率分布估计总体分布课件(共40张PPT)
文档属性
| 名称 | 2.2.1用样本的频率分布估计总体分布课件(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 325.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 20:44:00 | ||
图片预览








文档简介
课件40张PPT。用样本的频率分布估计总体分布(一) 【教学目标】
1.知识与技能
①在表示样本数据的过程中,学会列频率分布表,画频率分布直方图;
②能利用样本的频率分布估计总体分布
2.过程与方法
通过对现实生活数据的统计,进一步体会应用数学知识解决问题的方法.
3.情感、态度、价值观
通过对样本数据的分析,估计总体分布,认识到数学知识源于生活并指导生活的事实,体会数学知识与现实世界的联系.复习回顾抽样是统计的第一步,接下来就要对样本进行分析 通过图、表、计算来分析样本数据,找出数据中的规律,就可以对总体作出相应的估计.这种估计一般分成两种: ①是用样本的频率分布估计总体的分布. ②是用样本的数字特征(如平均数、标准差 等)估计总体的数字特征. 用样本去估计总体,是研究统计问题的一个基本思想. 初中时我们学习过样本的频率分布,包括频数、频率的概念,频率分布表的制作.频率分布 样本中所有数据(或数据组)的频数和样本容量的比,叫做该数据的频率.频率分布的表示形式有:
①样本频率分布表
②样本频率分布条形图
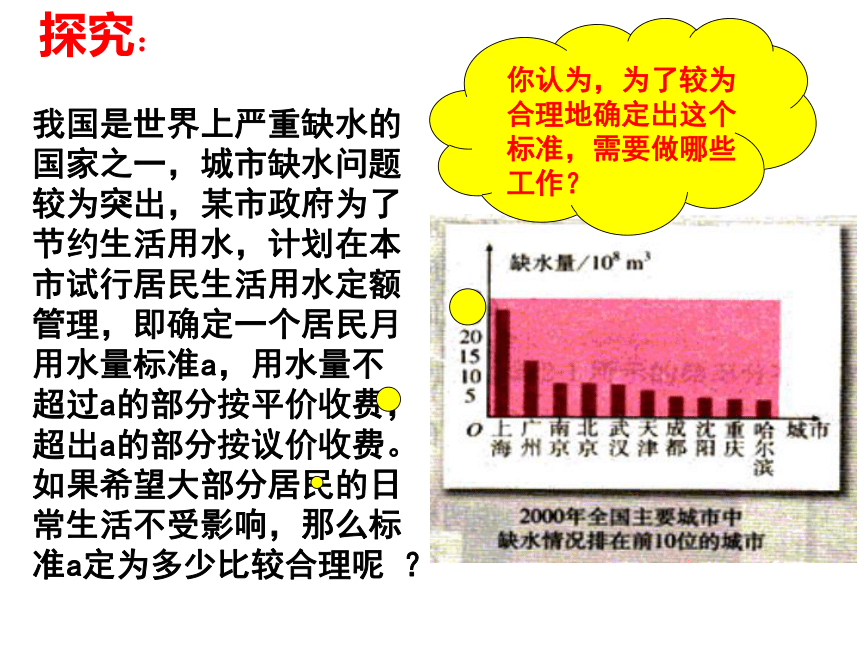
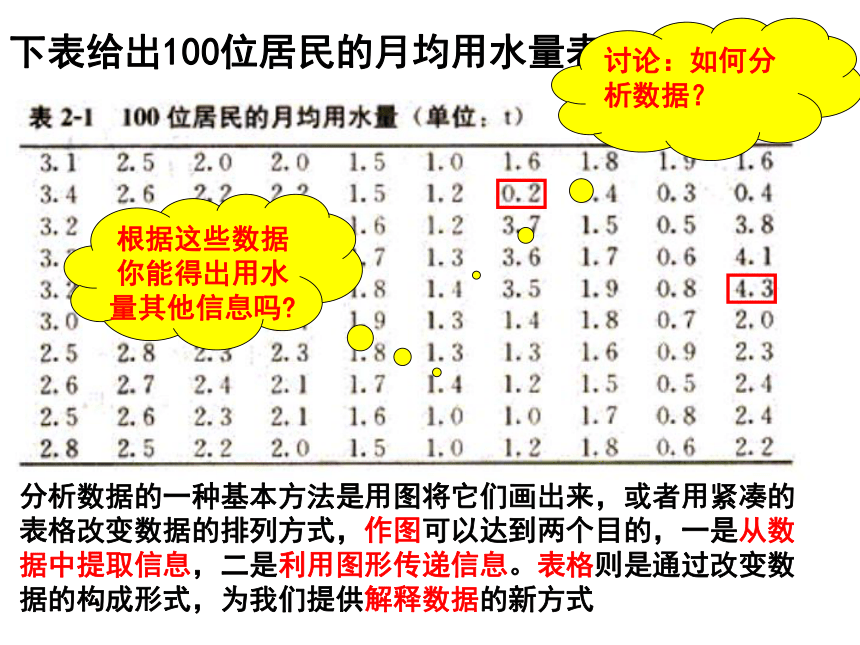
③样本频率分布直方图所有数据(或数据组)的频数的分布变化规律叫做样本的频率分布.我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费。如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢 ?探究:我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费。如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢 ?探究:下表给出100位居民的月均用水量表
分析数据的一种基本方法是用图将它们画出来,或者用紧凑的表格改变数据的排列方式,作图可以达到两个目的,一是从数据中提取信息,二是利用图形传递信息。表格则是通过改变数据的构成形式,为我们提供解释数据的新方式讨论:如何分析数据?根据这些数据你能得出用水量其他信息吗?〈一〉频率分布的概念:
频率分布是指一个样本数据在各个小范围内所占比例的大小。一般用频率分布直方图反映样本的频率分布. 〈二〉画频率分布直方图其一般步骤为
(1)计算一组数据中最大值与最小值的差,即求极差
(2)决定组距与组数
(3)将数据分组
(4)列频率分布表
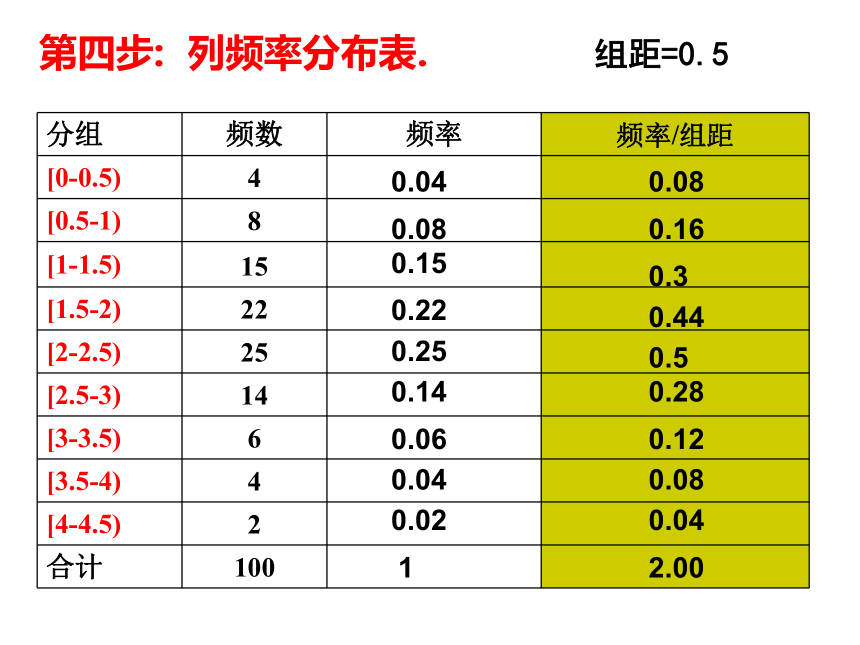
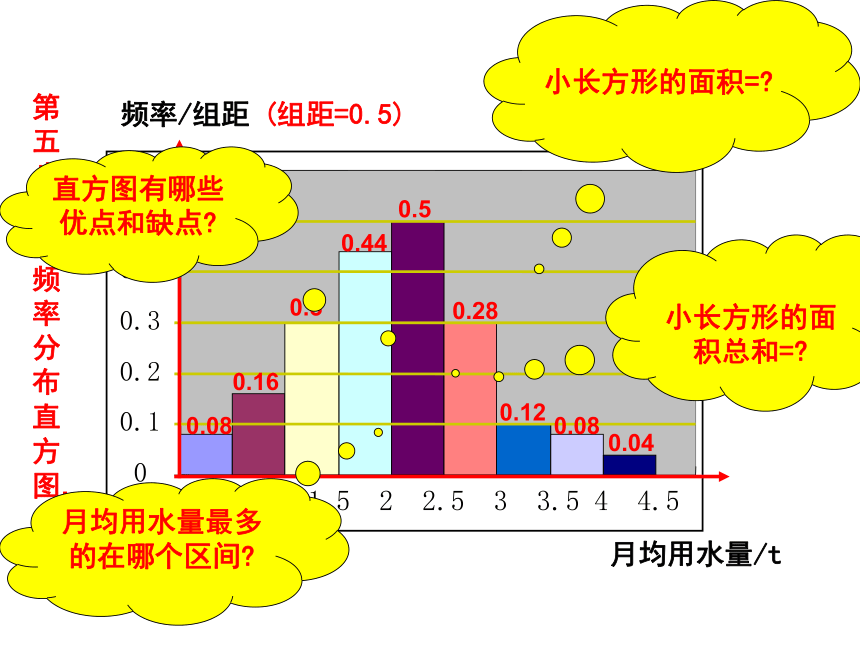
(5)画频率分布直方图第一步: 求极差: (数据组中最大值与最小值的差距) 最大值4.3 最小值0.2 所以极差 4.3-0.2 = 4.1第二步: 决定组距与组数: (强调取整) 第三步: 将数据分组:( 给出组的界限) [0, 0.5), [0.5, 1), [1, 1.5),……[4, 4.5] 共9组. 第四步: 列频率分布表. 组距=0.5 0.040.080.080.160.30.150.440.220.250.512.000.020.040.040.080.120.280.140.06第五步: 画出频率分布直方图. 频率/组距 月均用水量/t (组距=0.5)
小长方形的面积=?
小长方形的面积总和=?月均用水量最多的在哪个区间?直方图有哪些优点和缺点?频率分布直方图的特征:
从频率分布直方图可以清楚的看出数据分布的总体趋势。
从频率分布直方图得不出原始的数据内容,把数据表示成直方图后,原有的具体数据信息就被抹掉了。思考:
1.频率分布表与频率分布直方图的区别?频率分布表列出的是在各个不同区间内取值的频率。
频率分布直方图是用小长方形面积的大小来表示在各个区间内取值的频率。频率/组距 月均用水量/t (组距=0.5) 2.如果当地政府希望使85%以上的居民每月的用水量不
超出标准,根据频率分布表2-2和频率分布直方图
2.2-1,你能对制定月用水量标准提出建议吗 ?
同样一组数据,如果组距不同,横轴、纵轴的单位不同,得到的图的形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断。分别以1和0.1为组距重新作图,然后谈谈你对图的印象。 练 习:1.(导学案P78针对训练1)[40,50) 2[60,70) 10[80,90) 12[50,60) 3[70,80) 15[90,100) 8(1)列出样本的频率分布表;(2)画出频率分布直方图;练 习: 3.为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率分布直方图.图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组的频数为12.
(1)第二小组的频
率是多少?
(2)样本容量是多少?
(3)若次数在110以
上(含110次)为达
标,试估计该校全体
高一学生的达标率约
是多少?90 100 110 120 130 140 150次数o0.0040.0080.0120.0160.0200.0240.028频率/组距0.0320.036
4 .投掷一枚均匀骰子44次的记录是:现对这些数据进行整理,试画出频数分布条形图. 第二步:列出频率分布表:组距=1第三步: 画频率分布条形图第一步:写出样本可能出现的一切数值,即:
1,2,3,4,5,6 共6个数.(数据分组)课堂小结编制频率分布直方图的步骤:①找最大值与最小值。②决定组距与组数③决定分点④登记频数,计算频率,列表,画直方图用样本的频率分布估计总体分布
(二) 【教学目标】
1.知识与技能
(1)通过实例体会分布的意义和作用.
(2)在表示样本数据的过程中,学会列频率分布表,画频率分布直方图、频率折线图和茎叶图.
(3)通过实例体会频率分布直方图、频率分布折线图、茎叶图的各自特征,从而恰当地选择上述方法分析样本的分布,准确地做出总体估计.
2.过程与方法
通过对现实生活数据的统计,进一步体会应用数学知识解决问题的方法.
3.情感、态度、价值观
通过样本分析估计总体的过程,认识到数学知识源于生活并指导生活的事实,体会数学知识与现实世界的联系. 复 习 1.列出一组样本数据的频率分布直方图可以分哪几个步骤进行?第一步,求极差.第二步,决定组距与组数.第三步,确定分点,将数据分组.第四步,统计频数,计算频率,制成 表格. 2.频率分布直方图是在平面直角坐标系中画若干个依次相邻的小长方形,这些小长方形的宽、高和面积在数量上分别表示什么? 3.我们可以用样本数据的频率分布表和频率分布直方图估计总体的频率分布,当总体中的个体数较多或较少时,统计中用什么方法提取样本数据的相关信息,我们将进一步作些探究.组距、频率除以组距、频率.频率分布
折线图和茎叶图频率分布直方图如下:连接频率分布直方图中各小长方形上端的中点,得到频率分布折线图探究(一):频率分布折线图
利用样本频分布对总体分布进行估计(3)当样本容量无限增大,组距无限缩小,那么频率分布折线图就会无限接近于一条光滑曲线——总体密度曲线。(2)样本容量越大,这种估计越精确。(1)上例的样本容量为100,如果增至1000,其频率分布直方图的情况会有什么变化?假如增至10000呢?总体密度曲线月均用水量/tab (图中阴影部分的面积,表示总体在某个区间 (a, b) 内取值的百分比)。 用样本分布直方图去估计相应的总体分布时,一般样本容量越大,频率分布直方图越接近总体密度曲线,就越精确地反映了总体的分布规律,即越精确地反映了总体在各个范围内取值百分比。 总体密度曲线反映了总体在各个范围内取值的百分比,精确地反映了总体的分布规律。是研究总体分布的工具.总体密度曲线探究(二):茎叶图 频率分布表、频率分布直方图和折线图的主要作用是表示样本数据的分布情况,此外,我们还可以用茎叶图来表示样本数据的分布情况. 【问题】 某赛季甲、乙两名篮球运动员每场比赛的得分情况如下:
甲运动员得分:13,51,23,8,26,38,16,33,14,28,39;
乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39.助教在比赛中将这些数据记录为如下形式: 甲 乙 8
4 6 3
3 6 8
3 8 9
10
1
2
3
4
5 5
4
6 1 6 7 9
9
0茎叶图甲乙0
1
2
3
4
5
2 5
5 4
1 6 1 6 7 9
4 9
08
4 6 3
6 8
3 8 9
1 叶就是从茎的旁边生长出来的数,表示得分的个位数。 茎是指中间的一列数,表示得分的十位数思考1:你能理解这个图是如何记录这些数据的吗?你能通过该图说明哪个运动员的发挥更稳定吗? 思考2:对于样本数据:3.1,2.5,2.0,0.8,1.5,1.0,4.3,2.7,3.1,3.5,用茎叶图如何表示? 茎叶画茎叶图的步骤:第一步,将每个数据分为“茎”(高位)和“叶”(低位)两部分;第二步,将最小的茎和最大的茎之间的数按大小次序排成一列,写在左(右)侧;第三步,将各个数据的叶按大小次序写在茎右(左)侧. 茎叶图不仅能够保留原始数据,而且能够展示数据的分布情况。
在样本数据较少时,用茎叶图表示数据的效果较好。可以随时纪录,这对数据的纪录和表示都能带来方便。但当样本数据较多时,茎叶图就显得不太方便。因为每一个数据都要在茎叶图中占据一个空间,如果数据很多,枝叶就会很长。比较:练 习:1.(导学案P78例1)2.(导学案P78例2)分析:由于样本容量不大,所以画茎叶图方便。此时茎叶图不仅清晰明了的展示了数据分布情况,便于比较,且没有信息损失,而且还可以随时记录新数据。3.(导学案P79针对训练2)4.(导学案P79例3)课堂小结1.编制频率分布直方图的步骤:①找最大值与最小值。②决定组距与组数③决定分点④登记频数,计算频率,列表,画直方图2.频率分布折线图与总体密度曲线3.绘制茎叶图的步骤
1.知识与技能
①在表示样本数据的过程中,学会列频率分布表,画频率分布直方图;
②能利用样本的频率分布估计总体分布
2.过程与方法
通过对现实生活数据的统计,进一步体会应用数学知识解决问题的方法.
3.情感、态度、价值观
通过对样本数据的分析,估计总体分布,认识到数学知识源于生活并指导生活的事实,体会数学知识与现实世界的联系.复习回顾抽样是统计的第一步,接下来就要对样本进行分析 通过图、表、计算来分析样本数据,找出数据中的规律,就可以对总体作出相应的估计.这种估计一般分成两种: ①是用样本的频率分布估计总体的分布. ②是用样本的数字特征(如平均数、标准差 等)估计总体的数字特征. 用样本去估计总体,是研究统计问题的一个基本思想. 初中时我们学习过样本的频率分布,包括频数、频率的概念,频率分布表的制作.频率分布 样本中所有数据(或数据组)的频数和样本容量的比,叫做该数据的频率.频率分布的表示形式有:
①样本频率分布表
②样本频率分布条形图
③样本频率分布直方图所有数据(或数据组)的频数的分布变化规律叫做样本的频率分布.我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费。如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢 ?探究:我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费。如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢 ?探究:下表给出100位居民的月均用水量表
分析数据的一种基本方法是用图将它们画出来,或者用紧凑的表格改变数据的排列方式,作图可以达到两个目的,一是从数据中提取信息,二是利用图形传递信息。表格则是通过改变数据的构成形式,为我们提供解释数据的新方式讨论:如何分析数据?根据这些数据你能得出用水量其他信息吗?〈一〉频率分布的概念:
频率分布是指一个样本数据在各个小范围内所占比例的大小。一般用频率分布直方图反映样本的频率分布. 〈二〉画频率分布直方图其一般步骤为
(1)计算一组数据中最大值与最小值的差,即求极差
(2)决定组距与组数
(3)将数据分组
(4)列频率分布表
(5)画频率分布直方图第一步: 求极差: (数据组中最大值与最小值的差距) 最大值4.3 最小值0.2 所以极差 4.3-0.2 = 4.1第二步: 决定组距与组数: (强调取整) 第三步: 将数据分组:( 给出组的界限) [0, 0.5), [0.5, 1), [1, 1.5),……[4, 4.5] 共9组. 第四步: 列频率分布表. 组距=0.5 0.040.080.080.160.30.150.440.220.250.512.000.020.040.040.080.120.280.140.06第五步: 画出频率分布直方图. 频率/组距 月均用水量/t (组距=0.5)
小长方形的面积=?
小长方形的面积总和=?月均用水量最多的在哪个区间?直方图有哪些优点和缺点?频率分布直方图的特征:
从频率分布直方图可以清楚的看出数据分布的总体趋势。
从频率分布直方图得不出原始的数据内容,把数据表示成直方图后,原有的具体数据信息就被抹掉了。思考:
1.频率分布表与频率分布直方图的区别?频率分布表列出的是在各个不同区间内取值的频率。
频率分布直方图是用小长方形面积的大小来表示在各个区间内取值的频率。频率/组距 月均用水量/t (组距=0.5) 2.如果当地政府希望使85%以上的居民每月的用水量不
超出标准,根据频率分布表2-2和频率分布直方图
2.2-1,你能对制定月用水量标准提出建议吗 ?
同样一组数据,如果组距不同,横轴、纵轴的单位不同,得到的图的形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断。分别以1和0.1为组距重新作图,然后谈谈你对图的印象。 练 习:1.(导学案P78针对训练1)[40,50) 2[60,70) 10[80,90) 12[50,60) 3[70,80) 15[90,100) 8(1)列出样本的频率分布表;(2)画出频率分布直方图;练 习: 3.为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率分布直方图.图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组的频数为12.
(1)第二小组的频
率是多少?
(2)样本容量是多少?
(3)若次数在110以
上(含110次)为达
标,试估计该校全体
高一学生的达标率约
是多少?90 100 110 120 130 140 150次数o0.0040.0080.0120.0160.0200.0240.028频率/组距0.0320.036
4 .投掷一枚均匀骰子44次的记录是:现对这些数据进行整理,试画出频数分布条形图. 第二步:列出频率分布表:组距=1第三步: 画频率分布条形图第一步:写出样本可能出现的一切数值,即:
1,2,3,4,5,6 共6个数.(数据分组)课堂小结编制频率分布直方图的步骤:①找最大值与最小值。②决定组距与组数③决定分点④登记频数,计算频率,列表,画直方图用样本的频率分布估计总体分布
(二) 【教学目标】
1.知识与技能
(1)通过实例体会分布的意义和作用.
(2)在表示样本数据的过程中,学会列频率分布表,画频率分布直方图、频率折线图和茎叶图.
(3)通过实例体会频率分布直方图、频率分布折线图、茎叶图的各自特征,从而恰当地选择上述方法分析样本的分布,准确地做出总体估计.
2.过程与方法
通过对现实生活数据的统计,进一步体会应用数学知识解决问题的方法.
3.情感、态度、价值观
通过样本分析估计总体的过程,认识到数学知识源于生活并指导生活的事实,体会数学知识与现实世界的联系. 复 习 1.列出一组样本数据的频率分布直方图可以分哪几个步骤进行?第一步,求极差.第二步,决定组距与组数.第三步,确定分点,将数据分组.第四步,统计频数,计算频率,制成 表格. 2.频率分布直方图是在平面直角坐标系中画若干个依次相邻的小长方形,这些小长方形的宽、高和面积在数量上分别表示什么? 3.我们可以用样本数据的频率分布表和频率分布直方图估计总体的频率分布,当总体中的个体数较多或较少时,统计中用什么方法提取样本数据的相关信息,我们将进一步作些探究.组距、频率除以组距、频率.频率分布
折线图和茎叶图频率分布直方图如下:连接频率分布直方图中各小长方形上端的中点,得到频率分布折线图探究(一):频率分布折线图
利用样本频分布对总体分布进行估计(3)当样本容量无限增大,组距无限缩小,那么频率分布折线图就会无限接近于一条光滑曲线——总体密度曲线。(2)样本容量越大,这种估计越精确。(1)上例的样本容量为100,如果增至1000,其频率分布直方图的情况会有什么变化?假如增至10000呢?总体密度曲线月均用水量/tab (图中阴影部分的面积,表示总体在某个区间 (a, b) 内取值的百分比)。 用样本分布直方图去估计相应的总体分布时,一般样本容量越大,频率分布直方图越接近总体密度曲线,就越精确地反映了总体的分布规律,即越精确地反映了总体在各个范围内取值百分比。 总体密度曲线反映了总体在各个范围内取值的百分比,精确地反映了总体的分布规律。是研究总体分布的工具.总体密度曲线探究(二):茎叶图 频率分布表、频率分布直方图和折线图的主要作用是表示样本数据的分布情况,此外,我们还可以用茎叶图来表示样本数据的分布情况. 【问题】 某赛季甲、乙两名篮球运动员每场比赛的得分情况如下:
甲运动员得分:13,51,23,8,26,38,16,33,14,28,39;
乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39.助教在比赛中将这些数据记录为如下形式: 甲 乙 8
4 6 3
3 6 8
3 8 9
10
1
2
3
4
5 5
4
6 1 6 7 9
9
0茎叶图甲乙0
1
2
3
4
5
2 5
5 4
1 6 1 6 7 9
4 9
08
4 6 3
6 8
3 8 9
1 叶就是从茎的旁边生长出来的数,表示得分的个位数。 茎是指中间的一列数,表示得分的十位数思考1:你能理解这个图是如何记录这些数据的吗?你能通过该图说明哪个运动员的发挥更稳定吗? 思考2:对于样本数据:3.1,2.5,2.0,0.8,1.5,1.0,4.3,2.7,3.1,3.5,用茎叶图如何表示? 茎叶画茎叶图的步骤:第一步,将每个数据分为“茎”(高位)和“叶”(低位)两部分;第二步,将最小的茎和最大的茎之间的数按大小次序排成一列,写在左(右)侧;第三步,将各个数据的叶按大小次序写在茎右(左)侧. 茎叶图不仅能够保留原始数据,而且能够展示数据的分布情况。
在样本数据较少时,用茎叶图表示数据的效果较好。可以随时纪录,这对数据的纪录和表示都能带来方便。但当样本数据较多时,茎叶图就显得不太方便。因为每一个数据都要在茎叶图中占据一个空间,如果数据很多,枝叶就会很长。比较:练 习:1.(导学案P78例1)2.(导学案P78例2)分析:由于样本容量不大,所以画茎叶图方便。此时茎叶图不仅清晰明了的展示了数据分布情况,便于比较,且没有信息损失,而且还可以随时记录新数据。3.(导学案P79针对训练2)4.(导学案P79例3)课堂小结1.编制频率分布直方图的步骤:①找最大值与最小值。②决定组距与组数③决定分点④登记频数,计算频率,列表,画直方图2.频率分布折线图与总体密度曲线3.绘制茎叶图的步骤
