2020年中考数学二轮专项——二次函数与几何图形综合题(含答案)
文档属性
| 名称 | 2020年中考数学二轮专项——二次函数与几何图形综合题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 555.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 00:00:00 | ||
图片预览



文档简介
2020年中考数学二轮专项——二次函数与几何图形综合题
类型一 线段数量关系/最值问题
1. (2019滨州)如图①,抛物线y=-x2+x+4与y轴交于点A,与x轴交于点B,C,将直线AB绕点A逆时针旋转90°,所得直线与x轴交于点D.
(1)求直线AD的函数解析式;
(2)如图②,若点P是直线AD上方抛物线上的一个动点.
①当点P到直线AD的距离最大时,求点P的坐标和最大距离;
②当点P到直线AD的距离为eq \f(5,4)时,求sin∠PAD的值.
第1题图
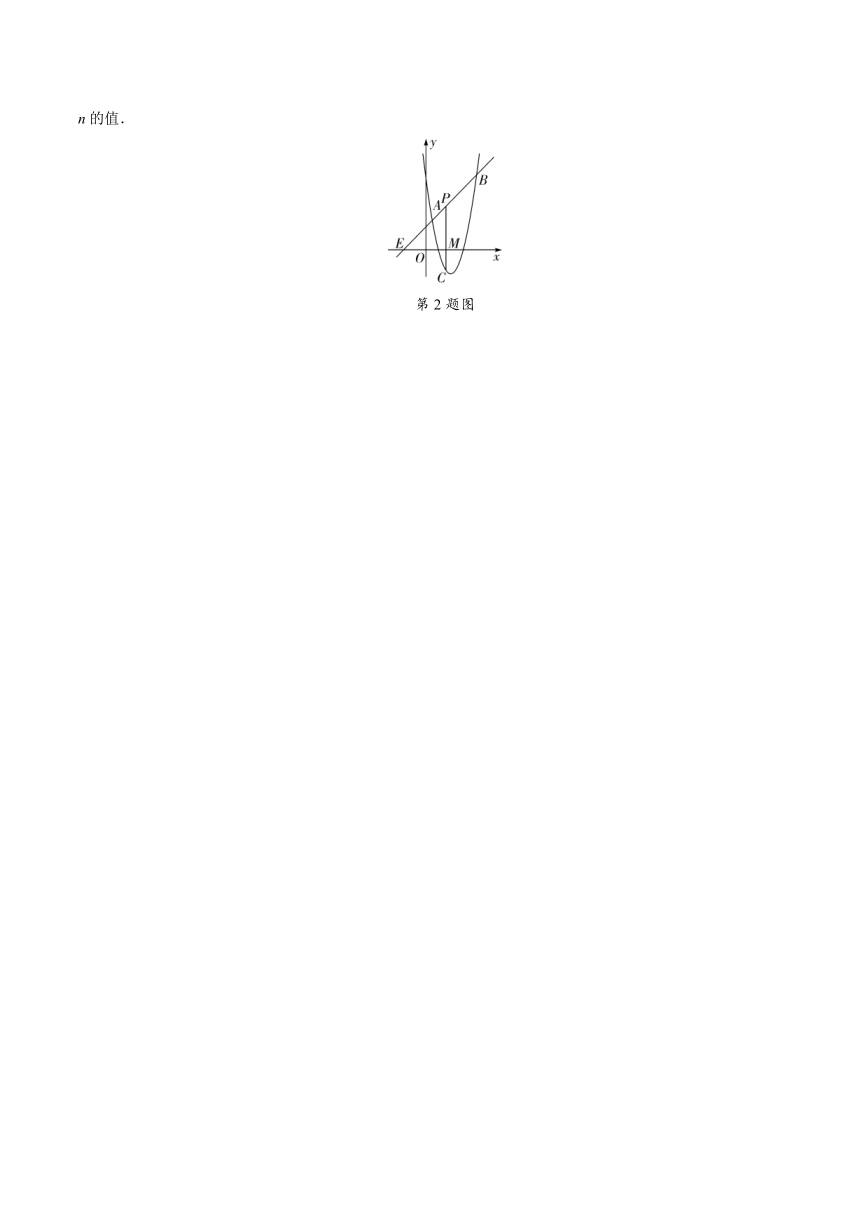
2. 如图,直线y=x+2与抛物线y=ax2+bx+6相交于A(,)和B(4,c).
(1)求抛物线的解析式;
(2)点P是直线AB上的动点,设点P的横坐标为n,过点P作PC⊥x轴,交抛物线于点C,交x轴于点M.
①当点P在线段AB上运动时(点P不与点A,B重合),是否存在这样的点P,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
②点P在直线AB上自由移动,当点C、P、M中恰有一点是其他两点所连线段的中点时,请直接写出n的值.
第2题图
类型二 面积数量关系/最值问题
1. (2019成华区一诊)如图,抛物线经过原点O,与x轴交于点A(-4,0),且经过点B(4,8).
(1)求抛物线的解析式;
(2)设直线y=kx+4与抛物线两交点的横坐标分别为x1,x2(x1
第1题图
。
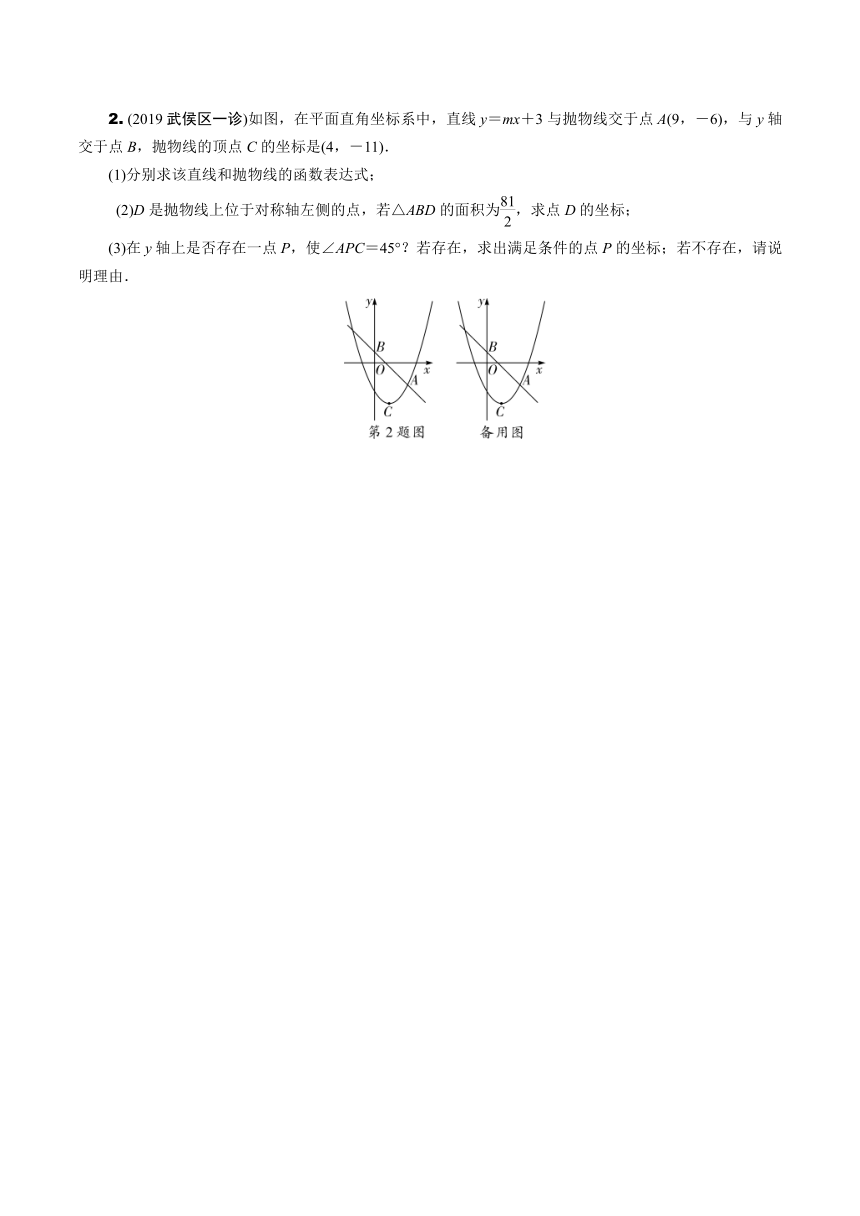
2. (2019武侯区一诊)如图,在平面直角坐标系中,直线y=mx+3与抛物线交于点A(9,-6),与y轴交于点B,抛物线的顶点C的坐标是(4,-11).
(1)分别求该直线和抛物线的函数表达式;
(2)D是抛物线上位于对称轴左侧的点,若△ABD的面积为,求点D的坐标;
(3)在y轴上是否存在一点P,使∠APC=45°?若存在,求出满足条件的点P的坐标;若不存在,请说明理由.
类型三 特殊三角形存在性问题
1. (2019武侯区二诊)如图,抛物线y=x2+(m+2)x+4的顶点C在x轴正半轴上,直线y=x+2与抛物线交于A,B两点(点A在点B的左侧).
(1)求抛物线的函数表达式;
(2)点P是抛物线上一点,若S△PAB=2S△ABC,求点P的坐标;
(3)将直线AB上下平移,平移后的直线y=x+t与抛物线交于A′、B′两点(A′在B′的左侧),当以点A′、B′、(2)中第二象限的点P为顶点的三角形是直角三角形时,求t的值.
类型四 特殊四边形存在性问题
1. (2019高新区二诊)如图,在同一直角坐标系中,抛物线C1:y=ax2-2x-3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧,交y轴于点D.
(1)求A、B两点的坐标;
(2)过抛物线C2:y=x2+mx+n在第三象限上的一点P,作PF⊥x轴于点F,交AD于点E,若E关于PD的对称点E′恰好落在y轴上,求P点的坐标;
(3)在抛物线C1上是否存在一点G,在抛物线C2上是否存在一点Q,使得以A、B、G、Q四点为顶点的四边形是平行四边形?若存在,求出G、Q两点的坐标;若不存在,请说明理由.
类型五 相似三角形问题
1. (2019金牛区一诊)如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
(1)求抛物线的解析式和顶点C的坐标;
(2)连接AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;
(3)若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.
第1题图 备用图
参考答案
类型一 线段数量关系/最值问题
1. 解:(1)抛物线y=-x2+x+4,
令x=0,可得A点的坐标为(0,4),
令y=0,可得B点的坐标为(-4,0),C点的坐标为(8,0).
易得直线AB的函数解析式为y=x+4,
∵OA=OB,
∴∠BAO=45°.
又∵直线AD由直线AB逆时针旋转90°而来,
∴∠BAD=90°,
∴∠OAD=45°,△OAD为等腰直角三角形,
∴OD=OA=4,D(4,0),
易得直线AD的函数解析式为y=-x+4;
(2)①如解图①,过点P作PE⊥x轴交AD于点E,PF⊥AD于点F,
第1题解图①
易得△PEF为等腰直角三角形,
∴PF=PE,
∴当PE取得最大值时,PF取得最大值,
设P(x,-x2+x+4),
则E(x,-x+4),
∴PE=-x2+x+4-(-x+4)=-x2+x=-(x-6)2+,
∴当x=6时,PE有最大值,
此时PF有最大值,
∴当x=6时,-x2+x+4=,
∴当点P到直线AD的距离最大时,点P的坐标为(6,),最大距离为;
②如解图②,连接AP,过点P作PE⊥x轴,交AD于点E,PF⊥AD于点F,当点P到AD的距离为时,PF=,
则此时PE=PF=,
将PE=代入PE=-(x-6)2+中,
解得x1=10,x2=2,
∴此时点P的坐标为(10,-)或(2,),
当点P的坐标为(2,)时,AP==,
∴sin∠PAD==;
当点P的坐标为(10,-)时,
AP==,
∴sin∠PAD===.
综上,sin∠PAD的值是或.
第1题解图②
2. 解:(1)∵B(4,c)在直线y=x+2上,
∴c=6,则B(4,6),
∵A(,),B(4,6)在抛物线y=ax2+bx+6上,
∴,
解得,
故抛物线的解析式为y=2x2-8x+6;
(2)①存在.
设点P的坐标为(n,n+2)(
∵-2<0,
② n的值为或.
【解法提示】设P的坐标为(n,n+2),则点C的坐标为(n,2n2-8n+6),易知抛物线与x轴交点坐标为(1,0),(3,0),直线与x轴交点坐标为(-2,0).(Ⅰ)若M点为PC的中点,此时n<-2或1
1. 解:(1)∵抛物线经过原点O,
∴设抛物线的解析式为y=ax2+bx,
把点A(-4,0),B(4,8)代入,得,
解得,
∴抛物线的解析式为y=x2+x;
(2)联立,
消去y,得x2+(1-k)x-4=0,
∴x1+x2=4(k-1),x1x2=-16,
∵-=,
∴=,
即=,
解得k=3或k=-1,
经检验都符合题意,
∴k的值为3或-1;
(3)∵OB∥PC,S△POC∶S△BOC=1∶2,
∴PC∶OB=1∶2,
∵B(4,8),
∴OB=4,直线OB的解析式为y=2x,
∴PC=2,
设点P的坐标为(a,a2+a)(-4<a<0),直线PC的解析式为y=2x+t,
把P(a,a2+a)代入y=2x+t,整理得t=a2-a,
∴直线PC的解析式为y=2x+a2-a,
易得直线AB的解析式为y=x+4,
联立,
解得x=4+a-a2,
∴PC=(xC-xP)=×(4+a-a2-a)=2,
解得a=2(舍去)或a=-2,
将a=-2代入抛物线的解析式,得y=×(-2)2-2=2-2,
∴点P的坐标为(-2,2-2).
2. 解:(1)把点A(9,-6)代入y=mx+3中,
得m=-1,
∴直线的函数表达式为y=-x+3;
∵抛物线的顶点C的坐标是(4,-11)且过点A(9,-6),
设抛物线的函数表达式为y=a(x-4)2-11,
∴a(9-4)2-11=-6,
解得a=,
∴抛物线的函数表达式为y=(x-4)2-11=x2-x-;
(2)设点D的横坐标为n.∵抛物线对称轴为直线x=4,
∴分两种情况讨论
①当0<n<4时,如解图①,
过点D作x轴的垂线交直线AB于点E,
则D(n,n2-n-),E(n,-n+3),
∴DE=-n+3-(n2-n-)=-n2+n+,
∴S△ABD=S△BDE+S△ADE=DE·(xE-xB)+DE·(xA-xE)
=DE·(xA-xB)=(-n2+n+)×9=,
解得n1=(不合题意,舍去),n2=(不合题意,舍去);
第2题解图①
②当n<0时,如解图②,过点D作x轴的垂线交直线AB于点E,
S△ABD=S△ADE-S△BDE=DE·(xA-xE)-DE·(xB-xE)=DE·(xA-xB)=(-n2+n+)×9=,
解得n1=,n2=(不合题意,舍去).
当n=时,y=×()2-×-=.
∴D(,);
第2题解图②
(3)在y轴上存在一点P,使∠APC=45°,
如解图③,分别过点C、A作y轴、x轴的平行线,两线交于点G,则∠CGA=90°,
∵A、C的坐标分别为(9,-6),(4,-11),
∴点G的坐标为(4,-6).
∴GA=GC=5.
作以G为圆心,GA的长度为半径的圆,交y轴于点P,P′,连接AP、CP、AP′、P′C,此时∠APC=∠AP′C=∠CGA=45°,
∴GP=5.
设点P的坐标为(0,k),过点G作GH⊥y轴于点H,
则H(0,-6).
在Rt△PGH中,PH2+HG2=PG2,
即(k+6)2+42=52,
解得k1=-3,k2=-9,
∴P(0,-3),P′(0,-9).
第2题解图③
类型三 特殊三角形存在性问题
1. 解:(1)∵抛物线的顶点C在x轴的正半轴上,
∴==0,
解得m=2或-6,
∵顶点在x轴正半轴上,
∴->0.解得m<-2,
∴m=-6,
∴抛物线的函数表达式为y=x2-4x+4;
(2)如解图①,过点C作抛物线的对称轴,交直线AB于点D,
由y=x2-4x+4得抛物线的对称轴是直线x=2,
则D(2,4),DC=4.
在点D上方的抛物线的对称轴上取一点E,使DE=2DC,
则E(2,12).
连接AE,BE,则S△ABE=2S△ABC.
过点E(2,12)作直线AB的平行线交抛物线于点P1,P2,
此时满足S△PAB=S△ABE=2S△ABC.
设直线P1P2的函数表达式为y=x+k,
∵点E(2,12)在直线P1P2上,
∴2+k=12,
∴k=10.
∴直线P1P2的函数表达式为y=x+10.
联立,
解得或,
综上所述,满足条件的点P的坐标为(-1,9),(6,16);
第1题解图①
(3)设A′(x1,y1),B′(x2,y2),
显然,∠PA′B′≠90°.
①如解图②,当∠A′B′P=90°时,过点B′作直线MN∥y轴,A′M⊥MN于点M,PN⊥MN于点N,
∵直线A′B′的解析式是y=x+t,
∴∠B′A′M=45°,
∴△A′B′M和△PB′N都是等腰直角三角形,
∴PN=NB′,
∴x2+1=9-y2,即x2+y2=8,
联立,
解得,
将点(4-t,4+t)代入抛物线的函数表达式,得4+t=(4-t)2-4×(4-t)+4.
解得 t1=0,t2=10(此时点A′与点P重合,舍去);
第1题解图②
如解图③,若∠A′PB′=90°,过点P作EF∥y轴,A′E⊥EF于E,B′F⊥EF于点F,
则△A′EP∽△PFB′,
∴=.
∴=.
∴x1x2+(x1+x2)+1=9(y1+y2)-y1y2-81,
令x2-4x+4=x+t,即x2-5x+4-t=0,
则x1+x2=5,x1x2=4-t,
y1+y2=(x1+t)+(x2+t)=x1+x2+2t=5+2t,
y1y2=(x1+t)(x2+t)=x1x2+t(x1+x2)+t2=t2+4t+4,
∴(4-t)+5+1=9(5+2t)-(t2+4t+4)-81,
整理得t2-15t+50=0,
解得t1=5,t2=10(此时A′与P重合,舍去),
综上,t的值为0或5.
第1题解图③
类型四 特殊四边形存在性问题
1. 解:(1)∵C1、C2关于y轴对称,
∴C1与C2的交点一定在y轴上,且C1与C2的形状,大小均相同,
∴a=1,n=-3,
∴C1的对称轴为直线x=1,
∴C2的对称轴为直线x=-1,
∴m=2,
∴C1的函数表达式为y=x2-2x-3,C2的函数表达式为y=x2+2x-3=0,
在C2的函数表达式y=x2+2x-3中,当y=0可得x2+2x-3=0,
解得x=-3或x=1,
∴A(-3,0),B(1,0);
(2)根据题意可得点D的坐标为(0,-3),设直线AD的表达式为y=kx+b.
把(0,-3)和(-3,0)代入到y=kx+b中得,
解得,
∴直线AD的表达式为y=-x-3,
设P(a,a2+2a-3),
则E(a,-a-3),
则PE=-a-3-(a2+2a-3)=-a2-3a,根据对称可得四边形PEDE′是菱形,则DE′=PE=-a2-3a,
如解图,过点P作PG⊥y轴于点G,
∵ED∥PE′,ED所在直线斜率k=-1
∴∠E′=∠AEF=45°,GE′=-a,PG=GE′.
在Rt△PGE′中,根据勾股定理得:PE′=-a,根据菱形性质可得:PE′=DE′,
∴-a=-a2-3a,
解得a=-3,
∴P(-3,2-4);
第1题解图
(3)存在.
∵AB的中点为(-1,0),且点G在抛物线C1上,点Q在抛物线C2上,
∴AB只能为平行四边形的一边,
∴GQ∥AB且GQ=AB,
由(1)可知AB=1-(-3)=4,
∴GQ=4,
设G(t,t2-2t-3),则Q(t+4,t2-2t-3)或(t-4,t2-2t-3),
①当Q(t+4,t2-2t-3)时,则t2-2t-3=(t+4)2+2(t+4)-3,
解得t=-2,
∴t2-2t-3=4+4-3=5,
∴G(-2,5),Q(2,5);
②当Q(t-4,t2-2t-3)时,则t2-2t-3=(t-4)2+2(t-4)-3,
解得t=2,
∴t2-2t-3=4-4-3=-3,
∴G(2,-3),Q(-2,-3),
综上可知,存在满足条件的点G、Q,其坐标为G(-2,5),Q(2,5)或G(2,-3),Q(-2,-3).
类型五 相似三角形问题
1. 解:(1)把点A、B、D的坐标分别代入抛物线的解析式中得:
,解得,
∴抛物线的解析式为y=-x2-2x+3,
∴抛物线的对称轴为直线x=-=-1,
∴点C的坐标为(-1,4);
(2)如解图①,过点C作CE∥AD交抛物线于点E,交y轴于点T,
则△ADE与△ACD面积相等,
直线AD过点D,设其解析式为y=mx+3,
将点A的坐标代入得:0=-3m+3,解得m=1,
则直线AD的解析式为y=x+3,
∵CE∥AD,设直线CE的解析式为y=x+n,
将点C的坐标代入上式得:4=-1+n,解得n=5,
则直线CE的解析式为y=x+5,
则点T的坐标为(0,5),
联立,
解得x=-1或x=-2(x=-1为点C的横坐标),
即点E的坐标为(-2,3);
在y轴取一点H′,使DT=DH′=2,
过点H′作直线E′E″∥AD,
则△ADE′和△ADE″都与△ACD面积相等,
同理可得直线E′E″的解析式为y=x+1,
联立,
解得x=,
∴点E″、E′的坐标分别为(,)、(,),
综上,满足要求的点E的坐标为(-2,3)或(,)或(,);
第1题解图①
(3)如解图②,设点P的坐标为(m,n),则n=-m2-2m+3,
把点C、D的坐标代入一次函数的解析式y=kx+b得:,
解得,
即直线CD的解析式为y=-x+3,
由(1)得,直线AD的解析式为y=x+3,
∴AD⊥CD,
而直线PQ⊥CD,故直线PQ的解析式中的k值与直线AD的解析式中的k值相同,
同理可得直线PQ的解析式为y=x+(n-m),
联立,
解得x=,
即点Q的坐标为(,),
则PQ2=(m-)2+(n-)2==(m+1)2·m2,
同理可得:PC2=(m+1)2[1+(m+1)2],
AH=2,CH=4,则AC=2,
当△ACH∽△CPQ时,==,
即4PC2=5PQ2,
整理得3m2+16m+16=0,
解得m=-4或m=-,
∴点P的坐标为(-4,-5)或(-,);
当△ACH∽△PCQ时,
同理可得,点P的坐标为(-,)或(2,-5),
综上所述,点P的坐标为(-4,-5)或(-,)或(-,)或(2,-5).
第1题解图②
针对训练
针对训练
针对训练
针对训练
针对训练
同课章节目录
