高中数学人教B版选修2-2 第一章 1.3.3导数的实际应用 上课课件(共40张PPT)
文档属性
| 名称 | 高中数学人教B版选修2-2 第一章 1.3.3导数的实际应用 上课课件(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 16:23:43 | ||
图片预览











文档简介
(共40张PPT)
1.3.3 导数的实际应用
生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题称为优化问题,优化问题有时也称为最值问题.解决这些问题具有非常重要的现实意义.
一般地,函数的单调性与导数的 关系:
在某个区间(a,b)内,如果 ,那么函数y=f(x)在这个区间内单调递增;如果 ,那么函数y=f(x)在这个区间内单调递减.
知识回顾
导数的单调性
新课导入
在过去的学习中,我们一般把优化问题转化为数学中的函数问题,进而转化为求函数的最值问题.
导数是求函数最大(小)值的强有力的工具.如何学以致用,利用导数求解优化问题呢?
1.3 生活中的优化问题举例
教学目标
知识与能力
能把背景性的问题结合生活经验通过分析问题逐步引入到数学问题中,熟悉数学建模的过程,培养发现问题、分析问题、解决问题的能力.
过程与方法
通过三个具有代表性的问题和对问题的深入分析,了解现实生活中存在的大量的优化问题,同时了解导数在解决优化问题中的作用.
情感态度与价值观
逐步培养学生养成运用数形结合、等价转化、函数与方程等数学思想方法思考问题、解决问题的习惯.
教学重难点
重点
能从实际问题的不同情景出发,建立与之相对应的函数关系.
难点
对问题深入细致的分析,完成数模转换.
例1 铁桶的最大容积:
把边长为a的正方形铁皮减去六个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正六棱柱形容器(不计接缝),设被剪去的四边形的AB边长为x,容器为V(x).求x为多少时,容器的容积最大?并求出最大容积.
A
D
C
B
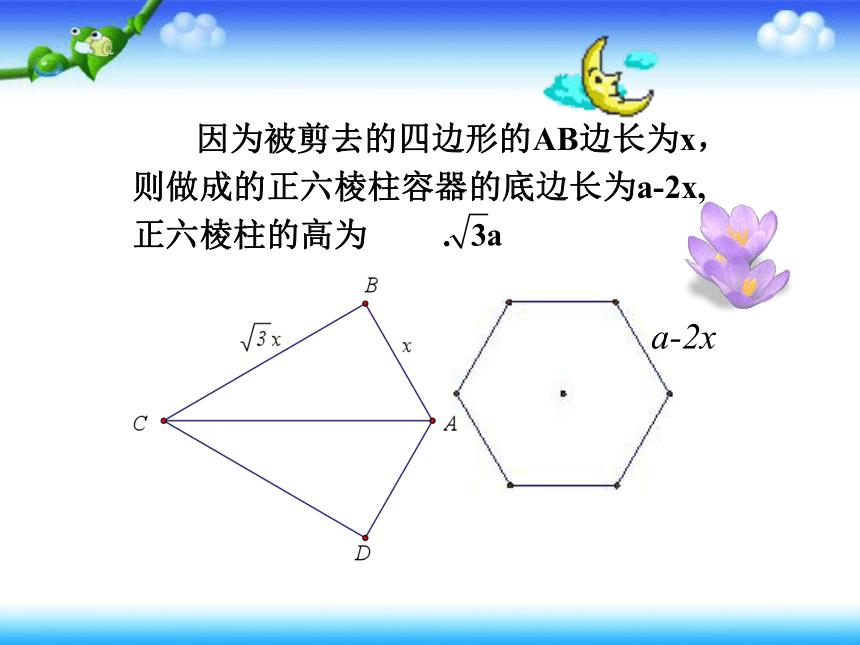
因为被剪去的四边形的AB边长为x,则做成的正六棱柱容器的底边长为a-2x,正六棱柱的高为 .
则:
实际问题归结为求函数V(x)在区间
上的最大值点.先求V(x)的极值点
在开区间 内,求导数得
令 ,即令
解得: (舍去)
因为在区间 内, 可能是极值点.
当 时, ;
当 时, .
因此 是极大值点,且在区间 内, 是唯一的极值点,所以 是V(x)的最大值点,并且最大值 即当 时,容器的容积最大为 .
例2 海报版面设计
学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示 的竖向张贴的海报,要求版心面积为128 ,上下两边各空2dm,左、右两边各空1dm.如何设计海报的尺寸,才能使四周空白面积最小?
解:设版心的高为x dm,则版心的宽为 dm,此时四周空白面积为
求导数,得
当x∈(0,16)时, 当x∈(16,+∞)时, .因此,x=16是函数S(x)的极小值点,也是最小值点.所以,当版心高为16dm,宽为8dm时,能使四周空白面积最小.
令
解得x=16(x=-16舍去)
于是宽为
例3 饮料瓶大小对饮料公司利润的影响
某制造商制造并出售球形瓶装的某种饮料.瓶子的制造成本是 分,其中r(单位:cm)是瓶子的半径.已知每售出1 mL的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为6 cm.
那么瓶子半径多大时,能使每瓶饮料的利润最大和最小?
解:由于瓶子的半径为r,所以每瓶饮料的利润是
令
当r=2时, ;当r∈(2,6)时,
因此,当半径r>2时, ,它表示f(r)单调递增,即半径越大,利润越高;半径r<2时, ,它表示f(r)单调递减,即半径越大,利润越低.
半径为2 cm时,利润最小,这时 表示此种瓶内饮料的利润还不够瓶子的成本,此时利润为负.
半径为6 cm时,利润最大.
我们不用导数工具,直接从函数的图象上观察,你能发现什么?
2
3
y
x
o
从图象上容易看出,当r=3时,f(3)=0,即瓶子的半径是3 cm时,饮料的利润与饮料瓶的成本恰好相等;当r>3时,利润才为正值.
当r∈(0,2)时,f(r)是减函数,你能解释它的实际意义吗?
并不是瓶子越小,利润越大.当瓶子半径在(0,2)之间时,每瓶容量受限,导致售出的饮料量减少,或者人们不想买太小瓶的饮料,而影响利润.
例4 磁盘的最大存储量问题
计算机把信息存储到磁盘上,磁盘是带有磁性介质的圆盘,并由操作系统将其格式化成磁道和扇区.磁道是指不同半径所构成的同心圆轨道,扇区是指被圆心角分割成的扇形区域.磁道上的定长的弧可作为基本存储单元,根据其磁化与否可分别记录数据0或1,几个基本单元通常称为比特(bit).
知识点
现有一张半径为R的磁盘,它的存储区是半径介于r与R的环形区域.
是不是r越小,磁盘的存储量越大?
R为多少时,磁盘具有最大存储量(最外面的磁道不存在任何信息)
为保障磁盘分辨率,磁道之间的宽度必须大于m,每比特所占用的磁道长度不得小于n.磁盘格式化时要求所有磁道具有相同的比特数.
设存储区的半径介于r与R之间,由于磁道之间的宽度必须大于m,且最外面的磁道不存储任何信息,所以磁道数最多可达到 .又由于每条磁道上的比特数相同,为获得最大的存储量,最内一条磁道必须装满,即每条磁道上的比特数可达到 .所以,磁盘总存储 量:
解:存储量=磁道数×每磁道的比特数
它是一个关于r的二次函数,从函数的解析式上可以判断,不是r越小,磁盘的存储量越大.
为求f(r)的最大值,计算
解得:
当 时, ;
当 时, .
因此,当 时,磁盘具有最大存储量,最大存储量为 .
优化问题
优化问题解决方案
用函数表示的数学问题
用导数解决数学问题
这是一个典型的数学建模过程
利用导数解决优化问题的基本思路:
建立数学模型
解决数学模型
作答
温馨提示:用导数解决实际问题,要特别注意在实际问题中变量的取值范围.
解决优化问题的一般步骤:
(1)审题
(2)建模
(3)解模
(4)回归
课堂小结
实际问题转化数学模型;
求解数学问题;
数学结果还原到实际问题之中
解决优化问题的步骤:
课堂习题
例1: 从长8cm,宽5cm的矩形薄铁板的四角剪去相等的正方形,做一个无盖的箱子,问剪去的正方形边长为多少时,箱子容积最大?最大容积是多少?
8cm
5cm
x
例2:统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: ( ),已知甲乙两地相距100千米,当汽车以多大速度行驶时,从甲地到乙地耗油最少?最少为多少升?
课堂答案
解:设剪去的正方形的边长为x cm,则箱子容积为:
令
得: (舍去)
例1
当0当1所以当x=1时, .
即剪去的正方形边剪去1 cm时,箱子的容积最大,其最大值是 .
解:当速度为x千米/小时,汽车从甲地到乙地行驶了 小时,设耗油量为h(x)升.
求函数的导数得:
例2
令 解得:
当x∈(0,80)时, ;
当x∈(80,120)时, .
∴在x=80时,取得极小值,也是最小值h(80)=11.25.
1.3.3 导数的实际应用
生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题称为优化问题,优化问题有时也称为最值问题.解决这些问题具有非常重要的现实意义.
一般地,函数的单调性与导数的 关系:
在某个区间(a,b)内,如果 ,那么函数y=f(x)在这个区间内单调递增;如果 ,那么函数y=f(x)在这个区间内单调递减.
知识回顾
导数的单调性
新课导入
在过去的学习中,我们一般把优化问题转化为数学中的函数问题,进而转化为求函数的最值问题.
导数是求函数最大(小)值的强有力的工具.如何学以致用,利用导数求解优化问题呢?
1.3 生活中的优化问题举例
教学目标
知识与能力
能把背景性的问题结合生活经验通过分析问题逐步引入到数学问题中,熟悉数学建模的过程,培养发现问题、分析问题、解决问题的能力.
过程与方法
通过三个具有代表性的问题和对问题的深入分析,了解现实生活中存在的大量的优化问题,同时了解导数在解决优化问题中的作用.
情感态度与价值观
逐步培养学生养成运用数形结合、等价转化、函数与方程等数学思想方法思考问题、解决问题的习惯.
教学重难点
重点
能从实际问题的不同情景出发,建立与之相对应的函数关系.
难点
对问题深入细致的分析,完成数模转换.
例1 铁桶的最大容积:
把边长为a的正方形铁皮减去六个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正六棱柱形容器(不计接缝),设被剪去的四边形的AB边长为x,容器为V(x).求x为多少时,容器的容积最大?并求出最大容积.
A
D
C
B
因为被剪去的四边形的AB边长为x,则做成的正六棱柱容器的底边长为a-2x,正六棱柱的高为 .
则:
实际问题归结为求函数V(x)在区间
上的最大值点.先求V(x)的极值点
在开区间 内,求导数得
令 ,即令
解得: (舍去)
因为在区间 内, 可能是极值点.
当 时, ;
当 时, .
因此 是极大值点,且在区间 内, 是唯一的极值点,所以 是V(x)的最大值点,并且最大值 即当 时,容器的容积最大为 .
例2 海报版面设计
学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示 的竖向张贴的海报,要求版心面积为128 ,上下两边各空2dm,左、右两边各空1dm.如何设计海报的尺寸,才能使四周空白面积最小?
解:设版心的高为x dm,则版心的宽为 dm,此时四周空白面积为
求导数,得
当x∈(0,16)时, 当x∈(16,+∞)时, .因此,x=16是函数S(x)的极小值点,也是最小值点.所以,当版心高为16dm,宽为8dm时,能使四周空白面积最小.
令
解得x=16(x=-16舍去)
于是宽为
例3 饮料瓶大小对饮料公司利润的影响
某制造商制造并出售球形瓶装的某种饮料.瓶子的制造成本是 分,其中r(单位:cm)是瓶子的半径.已知每售出1 mL的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为6 cm.
那么瓶子半径多大时,能使每瓶饮料的利润最大和最小?
解:由于瓶子的半径为r,所以每瓶饮料的利润是
令
当r=2时, ;当r∈(2,6)时,
因此,当半径r>2时, ,它表示f(r)单调递增,即半径越大,利润越高;半径r<2时, ,它表示f(r)单调递减,即半径越大,利润越低.
半径为2 cm时,利润最小,这时 表示此种瓶内饮料的利润还不够瓶子的成本,此时利润为负.
半径为6 cm时,利润最大.
我们不用导数工具,直接从函数的图象上观察,你能发现什么?
2
3
y
x
o
从图象上容易看出,当r=3时,f(3)=0,即瓶子的半径是3 cm时,饮料的利润与饮料瓶的成本恰好相等;当r>3时,利润才为正值.
当r∈(0,2)时,f(r)是减函数,你能解释它的实际意义吗?
并不是瓶子越小,利润越大.当瓶子半径在(0,2)之间时,每瓶容量受限,导致售出的饮料量减少,或者人们不想买太小瓶的饮料,而影响利润.
例4 磁盘的最大存储量问题
计算机把信息存储到磁盘上,磁盘是带有磁性介质的圆盘,并由操作系统将其格式化成磁道和扇区.磁道是指不同半径所构成的同心圆轨道,扇区是指被圆心角分割成的扇形区域.磁道上的定长的弧可作为基本存储单元,根据其磁化与否可分别记录数据0或1,几个基本单元通常称为比特(bit).
知识点
现有一张半径为R的磁盘,它的存储区是半径介于r与R的环形区域.
是不是r越小,磁盘的存储量越大?
R为多少时,磁盘具有最大存储量(最外面的磁道不存在任何信息)
为保障磁盘分辨率,磁道之间的宽度必须大于m,每比特所占用的磁道长度不得小于n.磁盘格式化时要求所有磁道具有相同的比特数.
设存储区的半径介于r与R之间,由于磁道之间的宽度必须大于m,且最外面的磁道不存储任何信息,所以磁道数最多可达到 .又由于每条磁道上的比特数相同,为获得最大的存储量,最内一条磁道必须装满,即每条磁道上的比特数可达到 .所以,磁盘总存储 量:
解:存储量=磁道数×每磁道的比特数
它是一个关于r的二次函数,从函数的解析式上可以判断,不是r越小,磁盘的存储量越大.
为求f(r)的最大值,计算
解得:
当 时, ;
当 时, .
因此,当 时,磁盘具有最大存储量,最大存储量为 .
优化问题
优化问题解决方案
用函数表示的数学问题
用导数解决数学问题
这是一个典型的数学建模过程
利用导数解决优化问题的基本思路:
建立数学模型
解决数学模型
作答
温馨提示:用导数解决实际问题,要特别注意在实际问题中变量的取值范围.
解决优化问题的一般步骤:
(1)审题
(2)建模
(3)解模
(4)回归
课堂小结
实际问题转化数学模型;
求解数学问题;
数学结果还原到实际问题之中
解决优化问题的步骤:
课堂习题
例1: 从长8cm,宽5cm的矩形薄铁板的四角剪去相等的正方形,做一个无盖的箱子,问剪去的正方形边长为多少时,箱子容积最大?最大容积是多少?
8cm
5cm
x
例2:统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: ( ),已知甲乙两地相距100千米,当汽车以多大速度行驶时,从甲地到乙地耗油最少?最少为多少升?
课堂答案
解:设剪去的正方形的边长为x cm,则箱子容积为:
令
得: (舍去)
例1
当0
即剪去的正方形边剪去1 cm时,箱子的容积最大,其最大值是 .
解:当速度为x千米/小时,汽车从甲地到乙地行驶了 小时,设耗油量为h(x)升.
求函数的导数得:
例2
令 解得:
当x∈(0,80)时, ;
当x∈(80,120)时, .
∴在x=80时,取得极小值,也是最小值h(80)=11.25.
