人教新课标A版高中数学三轮复习余弦定理课件 共46页ppt
文档属性
| 名称 | 人教新课标A版高中数学三轮复习余弦定理课件 共46页ppt |  | |
| 格式 | zip | ||
| 文件大小 | 874.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 16:28:03 | ||
图片预览



文档简介
(共46张PPT)
1
余弦定理
2
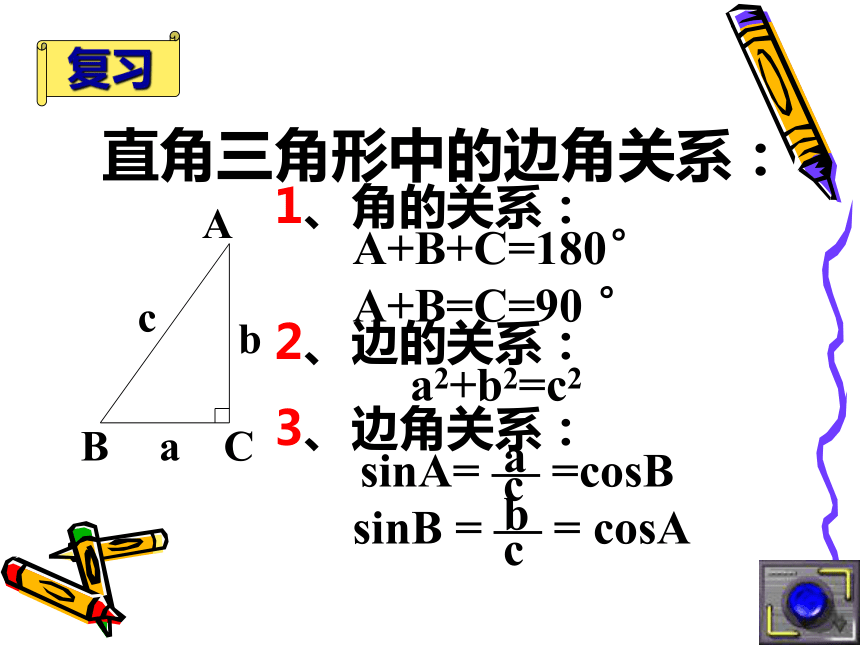
直角三角形中的边角关系:
C
B
A
a
b
c
1、角的关系:
A+B+C=180°
A+B=C=90 °
2、边的关系:
a2+b2=c2
3、边角关系:
sinA= — =cosB
sinB = — = cosA
a
c
b
c
复习
3
C
B
A
a
b
c
A
b
c
A
c
b
A
c
b
b
c
A
A
c
b
C
B
a
A
b
c
A
b
c
C
B
A
a
b
c
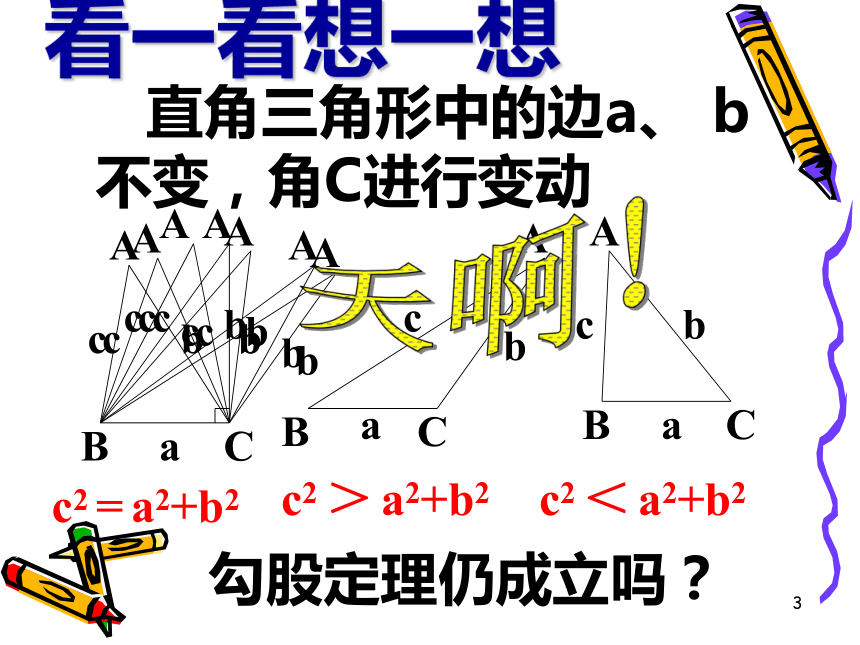
c2 > a2+b2
c2 < a2+b2
看一看想一想
直角三角形中的边a、 b不变,角C进行变动
勾股定理仍成立吗?
天啊!
c2 = a2+b2
4
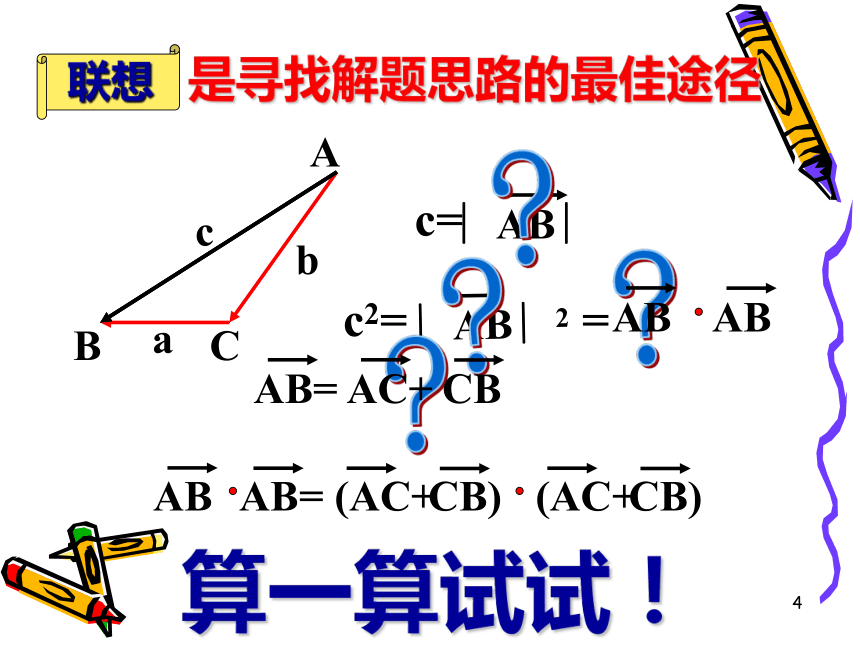
是寻找解题思路的最佳途径
c=
?
A
c
b
C
B
a
∣AB∣
c2=
∣AB∣2
=
?
?
AB
AB
AB=
?
AC+
CB
AB
AB=
(AC+
CB)
(AC+
CB)
算一算试试!
联想
5
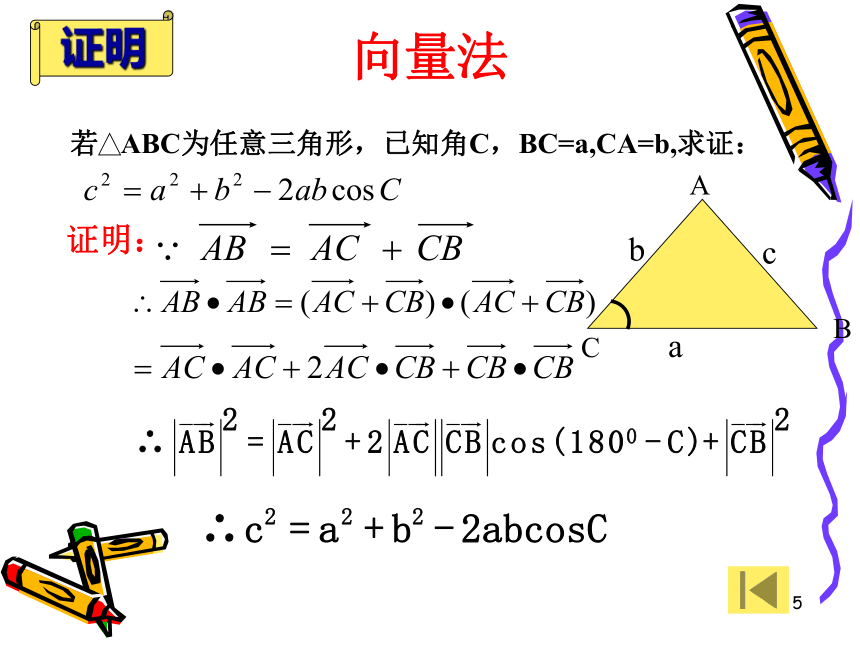
证明:
向量法
若 ABC为任意三角形,已知角C,BC=a,CA=b,求证:
b
c
A
B
C
a
证明
6
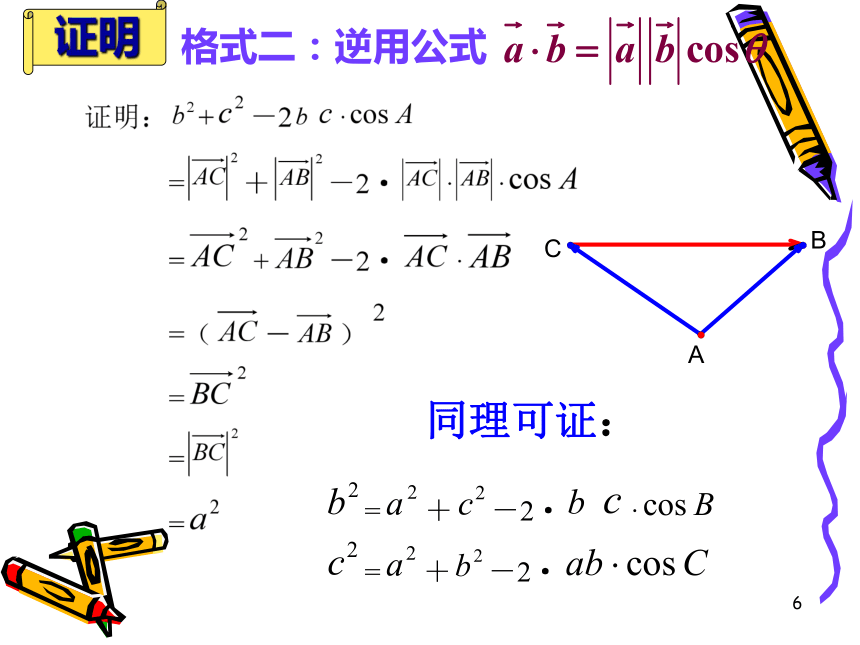
同理可证:
格式二:逆用公式
证明
7
b
A
a
c
C
B
证明:以CB所在的直线为x轴,过C点垂直于CB的直线为y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:
x
y
解析法
证明
8
A
B
C
a
b
c
D
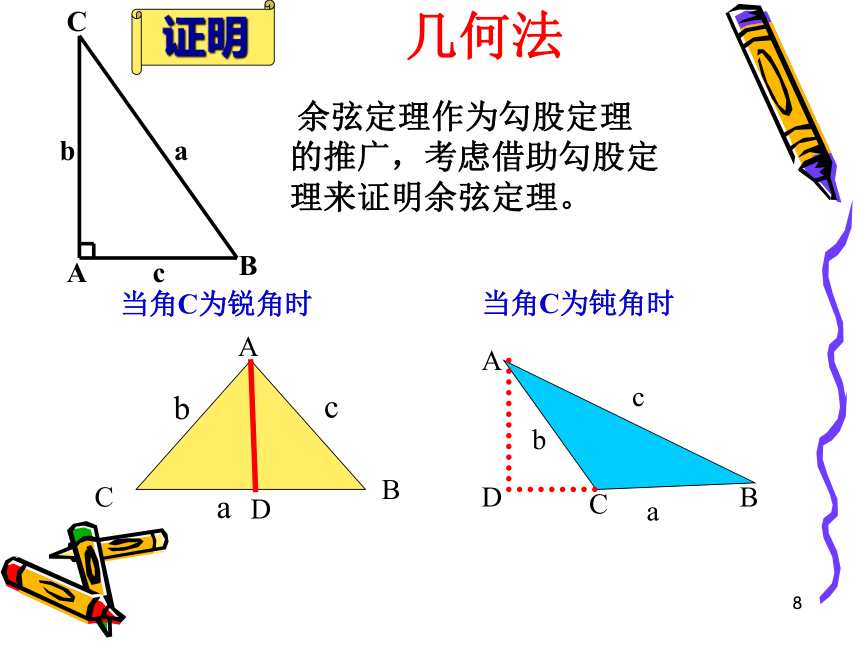
当角C为锐角时
几何法
b
A
a
c
C
B
D
当角C为钝角时
C
B
A
a
b
c
余弦定理作为勾股定理的推广,考虑借助勾股定理来证明余弦定理。
证明
9
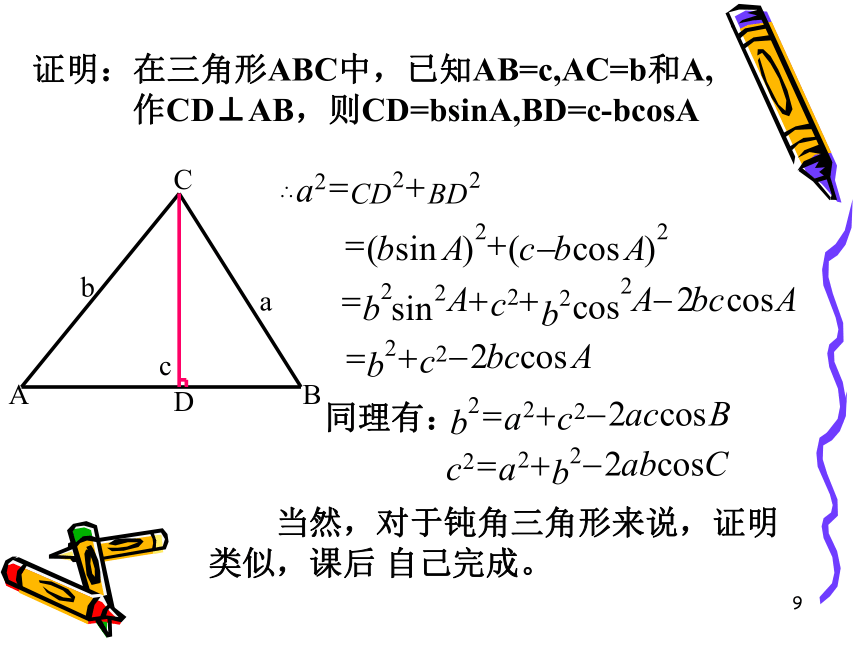
证明:在三角形ABC中,已知AB=c,AC=b和A,
作CD⊥AB,则CD=bsinA,BD=c-bcosA
A
B
C
c
b
a
同理有:
当然,对于钝角三角形来说,证明类似,课后 自己完成。
D
10
余弦定理
a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC
你能用文字说明吗?
C
B
A
a
b
c
三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
归纳
11
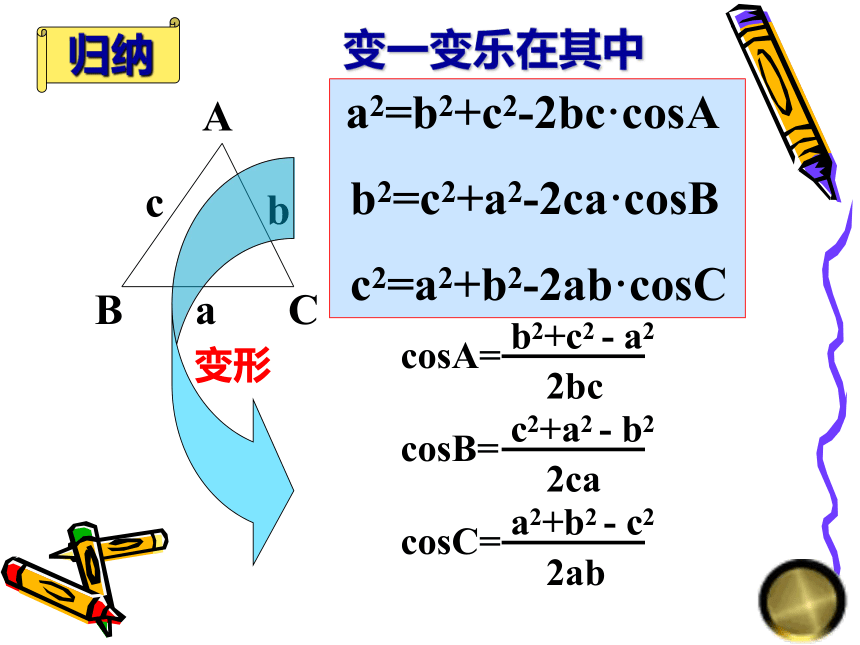
变一变乐在其中
C
B
A
a
b
c
a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC
b2+c2 - a2
2bc
cosA=
c2+a2 - b2
2ca
cosB=
a2+b2 - c2
2ab
cosC=
变形
归纳
12
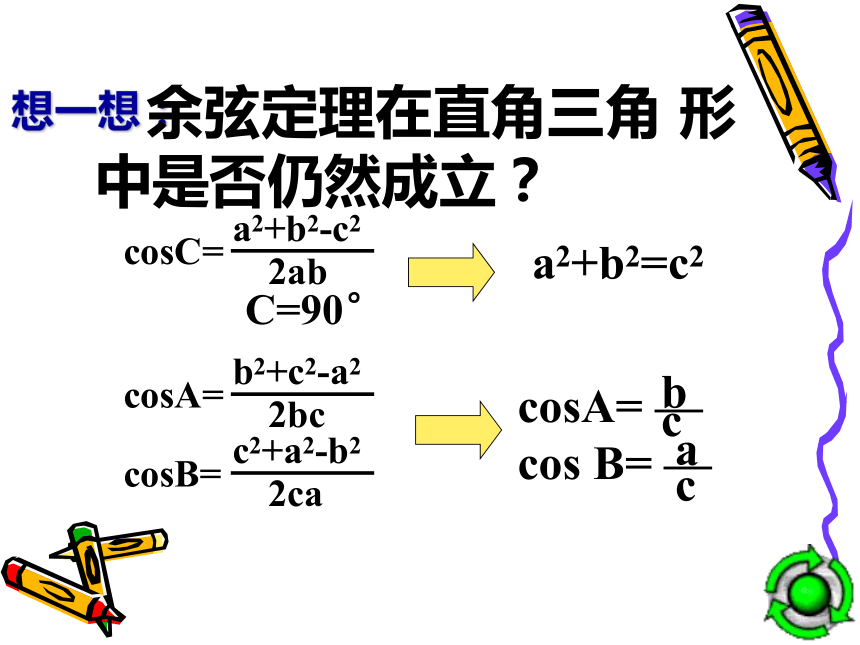
想一想:
余弦定理在直角三角 形中是否仍然成立?
cosC=
a2+b2-c2
2ab
C=90°
a2+b2=c2
cosA=
b2+c2-a2
2bc
cosB=
c2+a2-b2
2ca
cosA= —
cos B= —
a
c
b
c
13
问题1:勾股定理与余弦定理有何关系?
勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.
问题2:公式的结构特征怎样?
(1)轮换对称,简洁优美;
剖 析 定 理
(2)每个等式中有同一个三角形中的四个元素,知三求一.(方程思想)
剖析
14
思考:
已知两边及一边的对角时,我们知道可用正弦定理来解三角形,想一想能不能用余弦定理来解这个三角形?
如:已知b=4,c= ,C=60°求边a.
15
(3)已知a、b、c(三边),可以求什么?
剖 析 定 理
剖析
P14例3
P15练习2,3
16
剖 析 定 理
(4)能否把式子 转化为角的关系式?
分析:
剖析
17
(1)已知三边求三个角;
问题3:余弦定理在解三角形中的作用是什么?
(2)已知两边和它们的夹角,求第三边和其他两个角.
剖 析 定 理
剖析
P14例1、例2
18
19
会用才是真的掌握了
余弦定理在解三角形 中能解决哪些问题?
角边角
角角边
边边角
边角边
边边边
正弦定理
余弦定理
运用
20
练一练:P15练习1,4
1、已知△ABC的三边为 、2、1,求它的最大内角。
解:不妨设三角形的三边分别为a= ,b=2,c=1
则最大内角为∠A
由余弦定理
cosA=
12+22- ( ) 2
2×2×1
=
- —
1
2
∴ A=120°
变一变:
若已知三边的比是 :2:1,又怎么求?
21
再练:
2、已知△ABC中AB=2、AC=3、A= ,求BC的长。
解:由余弦定理可知
BC2=AB2+AC2-2AB×AC·cosA
=4+9-2×2×3×
=7
∴BC=
22
思考:
(1)在三角形ABC中,已知a=7,b=10,c=6,判定三角形ABC的形状
分析:三角形ABC的形状是由大边b所对的大角B决定的。
(2)在三角形ABC中,已知a=7,b=10,c=6,求三角形ABC的面积
分析:三角形的面积公式 S= absinC = bcsinA= acsinB, 只需先求出cosC(cosA或cosB),然后求出 sinC(sinA或 sinB)代入面积公式即可。
23
2.余弦定理
a =b +c-2bccosA
b =c +a-2accosB
c =a +b-2abcosC
2
2
2
2
2
2
2
2
2
3.由余弦定理知
1.证明定理:
课堂小结
向量法、解析法、几何法
24
(1)已知三边求三个角;
(2)已知两边和它们的夹角,求第三边和其他两个角.
5.余弦定理的作用
(3)判断三角形的形状,求三角形的面积
a =b +c-2bccosA
b =c +a-2accosB
c =a +b-2abcosC
2
2
2
2
2
2
2
2
2
4.余弦定理适用于任何三角形
25
作业布置
P16-17 1,5,6,10
26
例4 在长江某渡口处,江水以5km/h速度向东流。一渡船在江南岸的A码头出发,预定要在0.1h后到达江北岸码头(如图)。设AN为正北方向,已知B码头在A码头的北偏东15o,并与A码头相距1.2km.该渡船应按什么方向航行?速度是多少 千米/小时?(角度精确到0.1o,速度精确到0.1km/h)
27
P16练习1,2
28
练习:P16练习3,4
29
练习:P177,13
30
作业:P17 2,8,11,12
31
32
提高性训练:
1、在△ABC中,求证:c=acosB+bcosA
2、在△ABC中,若CB=7,AC=8,AB=9,求AB边的中线长。
33
例2、在三角形ABC中,已知a=2.730,b=3.696,c= ,
解这个三角形(边长保留四个有效数字,角度精确到 )
分析:已知两边和两边的夹角
解:
34
例 2:在?ABC中,已知a=2.730,b=3.696,
C=82°28′,解这个三角形.
解:
由 c2=a2+b2-2abcosC,
得 c≈4.297.
b2+c2-a2
2bc
∵ cosA= ≈0.7767,
∴ A≈39°2′,
∴ B=180°-(A+C)=58°30′.
a sinC
c
∵sinA= ≈0.6299,
∴ A=39°或141°(舍).
(
)
35
A
B
C
O
x
y
例 3:?ABC三个顶点坐标为(6,5)、
(-2,8)、(4,1),求A.
解法一:
∵ AB =√[6-(-2)]2+(5-8)2 =√73 ,
BC =√(-2-4)2+(8-1)2 =√85 ,
AC =√(6-4)2+(5-1)2=2√5 ,
cosA= = ,
2 AB AC
AB 2+ AC 2- BC 2
2
√365
∴
∴ A≈84°.
36
A
B
C
O
x
y
例 3:?ABC三个顶点坐标为(6,5)、
(–2,8)、(4,1),求A.
解法二:
∴ A≈84°.
∴ cosA=
=
= .
AB·AC
AB AC
(– 8)×(– 2)+3×(– 4)
√73·2√5
2
√365
∵ AB=(–8,3),AC=(–2,–4).
37
A
B
C
O
x
y
例 3:?ABC三个顶点坐标为(6,5)、
(–2,8)、(4,1),求A.
α
β
分析三: A = α+ β,
tanα = ?
tanβ = ?
tan(α+ β) =
38
解:
在?AOB中,
∵ |a – b|2 = |a|2+|b| 2 – 2|a||b|cos120°
=61,
∴ |a – b|=√61.
例 4:已知向量a、b夹角为120°,
且|a| =5,|b|=4,求|a – b| 、
|a+b| 及a+b与a的夹角.
a-b
a+b
B
b
A
C
a
120°
O
39
∴ a+b =√21.
∴ ∠COA即a+b与a的夹角约为49°.
∵ cos∠COA= ≈0.6546,
a 2+ a+b 2 – b 2
2 a a+b
例 4:已知向量a、b夹角为120°,
且|a| =5,|b|=4,求|a – b| 、
|a+b| 及a+b与a的夹角.
a-b
a+b
B
b
A
C
a
120°
O
在?OAC中,
∵ |a + b|2 = |a|2+|b| 2 – 2|a||b|cos60°
=21,
40
例5 已知四边形ABCD的四边长为AB = 2.4, BC = CD = DA = 1, A= 30°, 求C.
解: BD2 = AB2 + AD2 – 2AB·ADcosA
≈ 2.60,
cosC = = – 0.30,
DC2 + BC2 – BD2
2DC·BC
A
30°
D
C
B
C ≈ 107.5°.
思考:若A= θ, 怎样用θ表示四边形ABCD的面积?
41
练习
?ABC中,
(1)a=4,b=3,C=60°,则c=_____;
√13
14.6°
(2)a = 2, b = 3, c = 4, 则C = ______.
104.5°
(3)a=2,b=4,C=135°,则A=______.
42
研究题
总结解三角形的方法:已知三角形边角中哪三个量,有唯一解或多解或无解?分别用什么方法?
43
4、练习与思考:
44
45
在 中,以下的三角关系式,在解答有关三角形问题时,经常用到,要记熟并灵活地加以运用:
46
在 中,
在 中,已知(a+b+c)(a+b-c)=3ab
求角C=
在 中, 且 的面积为 ,则BC的长为
1
余弦定理
2
直角三角形中的边角关系:
C
B
A
a
b
c
1、角的关系:
A+B+C=180°
A+B=C=90 °
2、边的关系:
a2+b2=c2
3、边角关系:
sinA= — =cosB
sinB = — = cosA
a
c
b
c
复习
3
C
B
A
a
b
c
A
b
c
A
c
b
A
c
b
b
c
A
A
c
b
C
B
a
A
b
c
A
b
c
C
B
A
a
b
c
c2 > a2+b2
c2 < a2+b2
看一看想一想
直角三角形中的边a、 b不变,角C进行变动
勾股定理仍成立吗?
天啊!
c2 = a2+b2
4
是寻找解题思路的最佳途径
c=
?
A
c
b
C
B
a
∣AB∣
c2=
∣AB∣2
=
?
?
AB
AB
AB=
?
AC+
CB
AB
AB=
(AC+
CB)
(AC+
CB)
算一算试试!
联想
5
证明:
向量法
若 ABC为任意三角形,已知角C,BC=a,CA=b,求证:
b
c
A
B
C
a
证明
6
同理可证:
格式二:逆用公式
证明
7
b
A
a
c
C
B
证明:以CB所在的直线为x轴,过C点垂直于CB的直线为y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:
x
y
解析法
证明
8
A
B
C
a
b
c
D
当角C为锐角时
几何法
b
A
a
c
C
B
D
当角C为钝角时
C
B
A
a
b
c
余弦定理作为勾股定理的推广,考虑借助勾股定理来证明余弦定理。
证明
9
证明:在三角形ABC中,已知AB=c,AC=b和A,
作CD⊥AB,则CD=bsinA,BD=c-bcosA
A
B
C
c
b
a
同理有:
当然,对于钝角三角形来说,证明类似,课后 自己完成。
D
10
余弦定理
a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC
你能用文字说明吗?
C
B
A
a
b
c
三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
归纳
11
变一变乐在其中
C
B
A
a
b
c
a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC
b2+c2 - a2
2bc
cosA=
c2+a2 - b2
2ca
cosB=
a2+b2 - c2
2ab
cosC=
变形
归纳
12
想一想:
余弦定理在直角三角 形中是否仍然成立?
cosC=
a2+b2-c2
2ab
C=90°
a2+b2=c2
cosA=
b2+c2-a2
2bc
cosB=
c2+a2-b2
2ca
cosA= —
cos B= —
a
c
b
c
13
问题1:勾股定理与余弦定理有何关系?
勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.
问题2:公式的结构特征怎样?
(1)轮换对称,简洁优美;
剖 析 定 理
(2)每个等式中有同一个三角形中的四个元素,知三求一.(方程思想)
剖析
14
思考:
已知两边及一边的对角时,我们知道可用正弦定理来解三角形,想一想能不能用余弦定理来解这个三角形?
如:已知b=4,c= ,C=60°求边a.
15
(3)已知a、b、c(三边),可以求什么?
剖 析 定 理
剖析
P14例3
P15练习2,3
16
剖 析 定 理
(4)能否把式子 转化为角的关系式?
分析:
剖析
17
(1)已知三边求三个角;
问题3:余弦定理在解三角形中的作用是什么?
(2)已知两边和它们的夹角,求第三边和其他两个角.
剖 析 定 理
剖析
P14例1、例2
18
19
会用才是真的掌握了
余弦定理在解三角形 中能解决哪些问题?
角边角
角角边
边边角
边角边
边边边
正弦定理
余弦定理
运用
20
练一练:P15练习1,4
1、已知△ABC的三边为 、2、1,求它的最大内角。
解:不妨设三角形的三边分别为a= ,b=2,c=1
则最大内角为∠A
由余弦定理
cosA=
12+22- ( ) 2
2×2×1
=
- —
1
2
∴ A=120°
变一变:
若已知三边的比是 :2:1,又怎么求?
21
再练:
2、已知△ABC中AB=2、AC=3、A= ,求BC的长。
解:由余弦定理可知
BC2=AB2+AC2-2AB×AC·cosA
=4+9-2×2×3×
=7
∴BC=
22
思考:
(1)在三角形ABC中,已知a=7,b=10,c=6,判定三角形ABC的形状
分析:三角形ABC的形状是由大边b所对的大角B决定的。
(2)在三角形ABC中,已知a=7,b=10,c=6,求三角形ABC的面积
分析:三角形的面积公式 S= absinC = bcsinA= acsinB, 只需先求出cosC(cosA或cosB),然后求出 sinC(sinA或 sinB)代入面积公式即可。
23
2.余弦定理
a =b +c-2bccosA
b =c +a-2accosB
c =a +b-2abcosC
2
2
2
2
2
2
2
2
2
3.由余弦定理知
1.证明定理:
课堂小结
向量法、解析法、几何法
24
(1)已知三边求三个角;
(2)已知两边和它们的夹角,求第三边和其他两个角.
5.余弦定理的作用
(3)判断三角形的形状,求三角形的面积
a =b +c-2bccosA
b =c +a-2accosB
c =a +b-2abcosC
2
2
2
2
2
2
2
2
2
4.余弦定理适用于任何三角形
25
作业布置
P16-17 1,5,6,10
26
例4 在长江某渡口处,江水以5km/h速度向东流。一渡船在江南岸的A码头出发,预定要在0.1h后到达江北岸码头(如图)。设AN为正北方向,已知B码头在A码头的北偏东15o,并与A码头相距1.2km.该渡船应按什么方向航行?速度是多少 千米/小时?(角度精确到0.1o,速度精确到0.1km/h)
27
P16练习1,2
28
练习:P16练习3,4
29
练习:P177,13
30
作业:P17 2,8,11,12
31
32
提高性训练:
1、在△ABC中,求证:c=acosB+bcosA
2、在△ABC中,若CB=7,AC=8,AB=9,求AB边的中线长。
33
例2、在三角形ABC中,已知a=2.730,b=3.696,c= ,
解这个三角形(边长保留四个有效数字,角度精确到 )
分析:已知两边和两边的夹角
解:
34
例 2:在?ABC中,已知a=2.730,b=3.696,
C=82°28′,解这个三角形.
解:
由 c2=a2+b2-2abcosC,
得 c≈4.297.
b2+c2-a2
2bc
∵ cosA= ≈0.7767,
∴ A≈39°2′,
∴ B=180°-(A+C)=58°30′.
a sinC
c
∵sinA= ≈0.6299,
∴ A=39°或141°(舍).
(
)
35
A
B
C
O
x
y
例 3:?ABC三个顶点坐标为(6,5)、
(-2,8)、(4,1),求A.
解法一:
∵ AB =√[6-(-2)]2+(5-8)2 =√73 ,
BC =√(-2-4)2+(8-1)2 =√85 ,
AC =√(6-4)2+(5-1)2=2√5 ,
cosA= = ,
2 AB AC
AB 2+ AC 2- BC 2
2
√365
∴
∴ A≈84°.
36
A
B
C
O
x
y
例 3:?ABC三个顶点坐标为(6,5)、
(–2,8)、(4,1),求A.
解法二:
∴ A≈84°.
∴ cosA=
=
= .
AB·AC
AB AC
(– 8)×(– 2)+3×(– 4)
√73·2√5
2
√365
∵ AB=(–8,3),AC=(–2,–4).
37
A
B
C
O
x
y
例 3:?ABC三个顶点坐标为(6,5)、
(–2,8)、(4,1),求A.
α
β
分析三: A = α+ β,
tanα = ?
tanβ = ?
tan(α+ β) =
38
解:
在?AOB中,
∵ |a – b|2 = |a|2+|b| 2 – 2|a||b|cos120°
=61,
∴ |a – b|=√61.
例 4:已知向量a、b夹角为120°,
且|a| =5,|b|=4,求|a – b| 、
|a+b| 及a+b与a的夹角.
a-b
a+b
B
b
A
C
a
120°
O
39
∴ a+b =√21.
∴ ∠COA即a+b与a的夹角约为49°.
∵ cos∠COA= ≈0.6546,
a 2+ a+b 2 – b 2
2 a a+b
例 4:已知向量a、b夹角为120°,
且|a| =5,|b|=4,求|a – b| 、
|a+b| 及a+b与a的夹角.
a-b
a+b
B
b
A
C
a
120°
O
在?OAC中,
∵ |a + b|2 = |a|2+|b| 2 – 2|a||b|cos60°
=21,
40
例5 已知四边形ABCD的四边长为AB = 2.4, BC = CD = DA = 1, A= 30°, 求C.
解: BD2 = AB2 + AD2 – 2AB·ADcosA
≈ 2.60,
cosC = = – 0.30,
DC2 + BC2 – BD2
2DC·BC
A
30°
D
C
B
C ≈ 107.5°.
思考:若A= θ, 怎样用θ表示四边形ABCD的面积?
41
练习
?ABC中,
(1)a=4,b=3,C=60°,则c=_____;
√13
14.6°
(2)a = 2, b = 3, c = 4, 则C = ______.
104.5°
(3)a=2,b=4,C=135°,则A=______.
42
研究题
总结解三角形的方法:已知三角形边角中哪三个量,有唯一解或多解或无解?分别用什么方法?
43
4、练习与思考:
44
45
在 中,以下的三角关系式,在解答有关三角形问题时,经常用到,要记熟并灵活地加以运用:
46
在 中,
在 中,已知(a+b+c)(a+b-c)=3ab
求角C=
在 中, 且 的面积为 ,则BC的长为
同课章节目录
