人教A版高中数学选修4-7 第一讲 优选法 五 其它几种常用的优选法 上课课件(共39张PPT)
文档属性
| 名称 | 人教A版高中数学选修4-7 第一讲 优选法 五 其它几种常用的优选法 上课课件(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1003.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-18 11:19:41 | ||
图片预览











文档简介
(共39张PPT)
知识回顾
(1) 分数法的基本概念.
(2) 什么是斐波那契数列.
(3)分数法解决实际优选问题的操作步骤.
(4) 分数法的最优性.
新课导入
在前面几节中 我们介绍了黄金分割法、分数法等解决优选问题的优选法,但有些问题这些方法都不太适用,那么有没有其他更简单有效的方法呢?
想一想
案例1
有一条10km长的输电线路出现了故障,在线路的一端A处有电,在另一端B处没有电,要迅速查出故障所在位置.
这个问题,大多数同学想的都是用0.618法和分数法,这两种方法都是先做两个试验,然后通过比较,确定存优范围,不断将试验范围缩小,最后找到最佳点.两个试验太麻烦了,有没有更简单的方法呢?
下面我们介绍另外几种常用的优选法……
第一讲 优选法
第五讲 其他几种常用的优选法
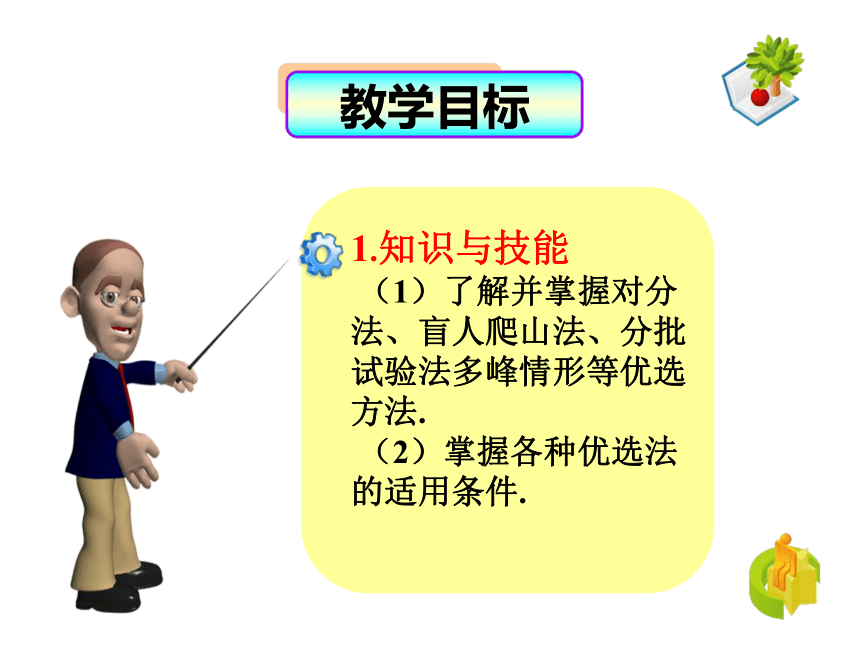
教学目标
1.知识与技能
(1)了解并掌握对分法、盲人爬山法、分批试验法多峰情形等优选方法.
(2)掌握各种优选法的适用条件.
2.过程与方法
讲述各种对分法、盲人爬山法、分批试验法多峰情形等的具体操作方法,使学生熟练掌握这几种优选法.
3.情感态度与价值观
让学生掌握对分法、盲人爬山法、分批试验法多峰情形等优选法的适用条件,培养解决问题的科学态度.
教学重难点
1.教学重点
使学生了解并熟练掌握对分法、盲人爬山法、分批试验法多峰情形等的具体操作方法及其使用条件.
2.教学难点
使学生熟练掌握对分法、盲人爬山法、分批试验法多峰情形等的使用条件.
本节导航
一、对分法
二、盲人爬山法
三、分批试验法
四、多峰情形
一、对分法
继续
根据案例1我们用对分法来进行解答:
分析:现在找输电线路故障所在位置,我们只需在AB之间的任意点C做检验,就能根据点C是否有电,判断出故障在哪一段,从而缩小故障范围,而不需要做两个实验进行比较.那么,如何选取检查点才能迅速找出故障位置呢?
继续解答……
由于在检查前无法预知检查结果,因此也就无法知道要排除的是检查点左边还是右边的线路.为了克服盲目性,我们把每次检查点安排在线路的中间,这样就可以去掉一般的长度.第一个检查点C安排在线路中间,如果有电,说明故障不在AC而在CB段,接着在CB中点D检查,如果没有电,说明在CD部分,再在CD中点E处检查,以此类推,很快就能找出故障的位置(图1-14)
图 1-14
注意
这个方法色要点是每个试点都去在因素范围的中点,将因素范围对分为两半,所以这个方法就称为对分法.用这种方法做试验的效果较0.618法好,每次可以去掉一半.
一般地,对分法可以按照如下步骤操作:
首先根据经验确定因素范围,设因素范围为[a,b].第一次试验在[a,b]中点x1(x1=(a+b)/2)处做.然后根据试验结果判断下次试验的方向,如果试验结果表明x1取小了,那么存优范围是[(a+b)/2,b],就把此次试点(中点)以下的因素范围[a, (a+b)/2)截去;如果试验结果表明x1取大了,那么存优范围是[a, (a+b)/2],
就把此次试点(中点)以上的因素范围((a+b)/2,b]截去.这样,每试验一次,存优范围就缩小了一半.重复上面的操作,即在存优范围的中点做试验,根据试验结果截去范围的一半,直到找出一个满意的试点,或存优范围已经变得足够小,再试下去结果无显著变化为止.
案例2
在商品价格竞猜游戏中,每一次试猜时,如何给出商品估价就可以最迅速地猜出真实价格.
解答:
因为每次给出估价都会得到“高了”或“低了”的提示语,于是我们可以根据提示语确定下一次该往高还是往低估.这说明可以用对分法给出商品估价,每次给出的估价都是存优区间的中点.每给一次估价,可以使价格范围缩小1/2,迅速猜中商品价格.
二 盲人爬山法
介绍
对要求我们在原有生产条件的基础上逐步探索,逐步提高,就像盲人爬山一样,在立足处,对前后两个方向进行试探,如果前面高了就向前走一步,否则试探后面,如果前后都比某点低,就说明到山顶了.
盲人爬山法的操作步骤是:
选找一个起点A(可以根据经验或估计),在A点做试验后可以向该因素的减少方向找一点B 做试验.如果好,就继续减少;如果不好就往增加方向找一点C 做试验,这样一步步地提高.
如果增加到E 点,再增加F点时反而坏了,这时可以从E点减少增加的步长,如果还是没有E点好,则E 就是该因素的最佳点(如图1-15).这就是单因素问题的盲人爬山法.
图 1-15
注意
盲人爬山法是一种采用小步调整策略的优选法,其依据的原理就是单峰函数的最佳点与好点在差点的同侧.
盲人爬山法的效果与起点关系很大,另外,每步间隔的大小,对试验效果关系也很大.在实践中往往采取“两头小,中间大”的办法.
三 分批试验法
案例3
电机修理厂根据原工艺要求,单晶切片厚度为0.54mm左右,经研磨损失0.15mm左右,1kg单晶只出12000左右小片.为了节约原材料、提高功效、降低成本,对减小单晶片厚度,在(0.20,0.40)范围内做优选法试验.切割不同厚度的单晶片很方便,但要检验究竟哪一种厚度好,则要经过磨片、化学腐蚀、烘干、烧结、参数测定等工序,试验周期长达三天(生产中则更长,要一个多星期),而且有些工序必须在同一条件下才能得到正确结果.
解答
为了加快试验进度,我们很容易想到把所有可能的试验同时安排进行,根据试验结果,找出最佳点.比较好的办法是全部试验分几批做,一批同时安排几个试验,同时进行比较,一批一批做下去,直到找出最佳点.这样可以兼顾试验设备、代价和时间上的要求.这种方法称为分批试验法.
继续
分批试验法可以分为均分分批试验法和比例分割分批试验法两种.
2.比例分割分批试验法
第一批
1.均分分批试验法
第一批
第二批
第二批
想一想
究竟一批安排几个试验合适呢?
这要根据具体情况而定.如果做一次试验很方便,消耗很少、时间很短;或检验很麻烦,时间又长;或代价很大,而且每次检验可以有好多样品同时进行,在这种情况下 每批试验可多做几个,即将试验范围分得细一些;否则就少做几个.
四 多峰情形
想一想
前面介绍的方法都只适用于“单峰”的情况.现实生产、生活中也经常碰到“多峰”的情形(图1-20),有时甚至连“单峰”还是 “多峰”都不知道,那又该如何下手呢?
f(x)
a
b
x
y
o
图 1-20
一般可采用以下两种方法:
(1)先不管它是“单峰”还是 “多峰”,用前面介绍的处理单峰的方法去做,找到一个“峰”后,如果达到预先要求,就选用于生产,以后再找其他更高的“峰”(即分区寻找).
(2)先做一批分布得比较均匀的试验,看它是否有“多峰”的现象.如果有,则分区寻找,在每个可能出现“高峰”的范围内做试验,把这些“峰”找出来。第一批分布均匀的试点最好以下述比例划分:α:β=0.618:0.382(图1-21).这样有峰值的范围总是成( α,β )或(β, α)形式,如图1-22.
α
β
α
β
图 1-21
α
β
β
α
图 1-22
课堂小结
1.本节所讲的对分法、盲人爬山法、分批试验法是本节课的重点,是单峰情形下的解决问题的方法.
2.多峰情形是对单峰情形的扩展.
课堂练习
练习1
分别用0.618法和对分法安排试验,找出蒸馒头时合适的放碱量,哪种方法会更有效呢?为什么?
解答
解答:
蒸馒头放碱问题,用对分法安排试验比用0.618法更有效.
分析:
这是因为:
第一,合适的放碱量事先有明确的标准,容易判断放碱量合适与否以及多或少;
第二,用0.618法需要相对准确的计量,对于这个问题似必要性不大;
第三,用对分法可以比用0.618法做较少次数的试验就能达到最佳点.
继续解答……
知识回顾
(1) 分数法的基本概念.
(2) 什么是斐波那契数列.
(3)分数法解决实际优选问题的操作步骤.
(4) 分数法的最优性.
新课导入
在前面几节中 我们介绍了黄金分割法、分数法等解决优选问题的优选法,但有些问题这些方法都不太适用,那么有没有其他更简单有效的方法呢?
想一想
案例1
有一条10km长的输电线路出现了故障,在线路的一端A处有电,在另一端B处没有电,要迅速查出故障所在位置.
这个问题,大多数同学想的都是用0.618法和分数法,这两种方法都是先做两个试验,然后通过比较,确定存优范围,不断将试验范围缩小,最后找到最佳点.两个试验太麻烦了,有没有更简单的方法呢?
下面我们介绍另外几种常用的优选法……
第一讲 优选法
第五讲 其他几种常用的优选法
教学目标
1.知识与技能
(1)了解并掌握对分法、盲人爬山法、分批试验法多峰情形等优选方法.
(2)掌握各种优选法的适用条件.
2.过程与方法
讲述各种对分法、盲人爬山法、分批试验法多峰情形等的具体操作方法,使学生熟练掌握这几种优选法.
3.情感态度与价值观
让学生掌握对分法、盲人爬山法、分批试验法多峰情形等优选法的适用条件,培养解决问题的科学态度.
教学重难点
1.教学重点
使学生了解并熟练掌握对分法、盲人爬山法、分批试验法多峰情形等的具体操作方法及其使用条件.
2.教学难点
使学生熟练掌握对分法、盲人爬山法、分批试验法多峰情形等的使用条件.
本节导航
一、对分法
二、盲人爬山法
三、分批试验法
四、多峰情形
一、对分法
继续
根据案例1我们用对分法来进行解答:
分析:现在找输电线路故障所在位置,我们只需在AB之间的任意点C做检验,就能根据点C是否有电,判断出故障在哪一段,从而缩小故障范围,而不需要做两个实验进行比较.那么,如何选取检查点才能迅速找出故障位置呢?
继续解答……
由于在检查前无法预知检查结果,因此也就无法知道要排除的是检查点左边还是右边的线路.为了克服盲目性,我们把每次检查点安排在线路的中间,这样就可以去掉一般的长度.第一个检查点C安排在线路中间,如果有电,说明故障不在AC而在CB段,接着在CB中点D检查,如果没有电,说明在CD部分,再在CD中点E处检查,以此类推,很快就能找出故障的位置(图1-14)
图 1-14
注意
这个方法色要点是每个试点都去在因素范围的中点,将因素范围对分为两半,所以这个方法就称为对分法.用这种方法做试验的效果较0.618法好,每次可以去掉一半.
一般地,对分法可以按照如下步骤操作:
首先根据经验确定因素范围,设因素范围为[a,b].第一次试验在[a,b]中点x1(x1=(a+b)/2)处做.然后根据试验结果判断下次试验的方向,如果试验结果表明x1取小了,那么存优范围是[(a+b)/2,b],就把此次试点(中点)以下的因素范围[a, (a+b)/2)截去;如果试验结果表明x1取大了,那么存优范围是[a, (a+b)/2],
就把此次试点(中点)以上的因素范围((a+b)/2,b]截去.这样,每试验一次,存优范围就缩小了一半.重复上面的操作,即在存优范围的中点做试验,根据试验结果截去范围的一半,直到找出一个满意的试点,或存优范围已经变得足够小,再试下去结果无显著变化为止.
案例2
在商品价格竞猜游戏中,每一次试猜时,如何给出商品估价就可以最迅速地猜出真实价格.
解答:
因为每次给出估价都会得到“高了”或“低了”的提示语,于是我们可以根据提示语确定下一次该往高还是往低估.这说明可以用对分法给出商品估价,每次给出的估价都是存优区间的中点.每给一次估价,可以使价格范围缩小1/2,迅速猜中商品价格.
二 盲人爬山法
介绍
对要求我们在原有生产条件的基础上逐步探索,逐步提高,就像盲人爬山一样,在立足处,对前后两个方向进行试探,如果前面高了就向前走一步,否则试探后面,如果前后都比某点低,就说明到山顶了.
盲人爬山法的操作步骤是:
选找一个起点A(可以根据经验或估计),在A点做试验后可以向该因素的减少方向找一点B 做试验.如果好,就继续减少;如果不好就往增加方向找一点C 做试验,这样一步步地提高.
如果增加到E 点,再增加F点时反而坏了,这时可以从E点减少增加的步长,如果还是没有E点好,则E 就是该因素的最佳点(如图1-15).这就是单因素问题的盲人爬山法.
图 1-15
注意
盲人爬山法是一种采用小步调整策略的优选法,其依据的原理就是单峰函数的最佳点与好点在差点的同侧.
盲人爬山法的效果与起点关系很大,另外,每步间隔的大小,对试验效果关系也很大.在实践中往往采取“两头小,中间大”的办法.
三 分批试验法
案例3
电机修理厂根据原工艺要求,单晶切片厚度为0.54mm左右,经研磨损失0.15mm左右,1kg单晶只出12000左右小片.为了节约原材料、提高功效、降低成本,对减小单晶片厚度,在(0.20,0.40)范围内做优选法试验.切割不同厚度的单晶片很方便,但要检验究竟哪一种厚度好,则要经过磨片、化学腐蚀、烘干、烧结、参数测定等工序,试验周期长达三天(生产中则更长,要一个多星期),而且有些工序必须在同一条件下才能得到正确结果.
解答
为了加快试验进度,我们很容易想到把所有可能的试验同时安排进行,根据试验结果,找出最佳点.比较好的办法是全部试验分几批做,一批同时安排几个试验,同时进行比较,一批一批做下去,直到找出最佳点.这样可以兼顾试验设备、代价和时间上的要求.这种方法称为分批试验法.
继续
分批试验法可以分为均分分批试验法和比例分割分批试验法两种.
2.比例分割分批试验法
第一批
1.均分分批试验法
第一批
第二批
第二批
想一想
究竟一批安排几个试验合适呢?
这要根据具体情况而定.如果做一次试验很方便,消耗很少、时间很短;或检验很麻烦,时间又长;或代价很大,而且每次检验可以有好多样品同时进行,在这种情况下 每批试验可多做几个,即将试验范围分得细一些;否则就少做几个.
四 多峰情形
想一想
前面介绍的方法都只适用于“单峰”的情况.现实生产、生活中也经常碰到“多峰”的情形(图1-20),有时甚至连“单峰”还是 “多峰”都不知道,那又该如何下手呢?
f(x)
a
b
x
y
o
图 1-20
一般可采用以下两种方法:
(1)先不管它是“单峰”还是 “多峰”,用前面介绍的处理单峰的方法去做,找到一个“峰”后,如果达到预先要求,就选用于生产,以后再找其他更高的“峰”(即分区寻找).
(2)先做一批分布得比较均匀的试验,看它是否有“多峰”的现象.如果有,则分区寻找,在每个可能出现“高峰”的范围内做试验,把这些“峰”找出来。第一批分布均匀的试点最好以下述比例划分:α:β=0.618:0.382(图1-21).这样有峰值的范围总是成( α,β )或(β, α)形式,如图1-22.
α
β
α
β
图 1-21
α
β
β
α
图 1-22
课堂小结
1.本节所讲的对分法、盲人爬山法、分批试验法是本节课的重点,是单峰情形下的解决问题的方法.
2.多峰情形是对单峰情形的扩展.
课堂练习
练习1
分别用0.618法和对分法安排试验,找出蒸馒头时合适的放碱量,哪种方法会更有效呢?为什么?
解答
解答:
蒸馒头放碱问题,用对分法安排试验比用0.618法更有效.
分析:
这是因为:
第一,合适的放碱量事先有明确的标准,容易判断放碱量合适与否以及多或少;
第二,用0.618法需要相对准确的计量,对于这个问题似必要性不大;
第三,用对分法可以比用0.618法做较少次数的试验就能达到最佳点.
继续解答……
