人教A版高中数学选修4-7 第一讲 优选法 二 单峰函数 上课课件(共32张PPT)
文档属性
| 名称 | 人教A版高中数学选修4-7 第一讲 优选法 二 单峰函数 上课课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-18 11:20:41 | ||
图片预览










文档简介
(共32张PPT)
一.了解并掌握优选法的概念.
二.学会查找最佳点的方法.
三.学会如何利用优选法解决优选问题.
知识回顾
记忆
新课导入
在军事训练中,经常要考虑发射角度多大时炮弹的射程情况.
下面,我们就以一实际炮弹射程问题进行进一步学习……
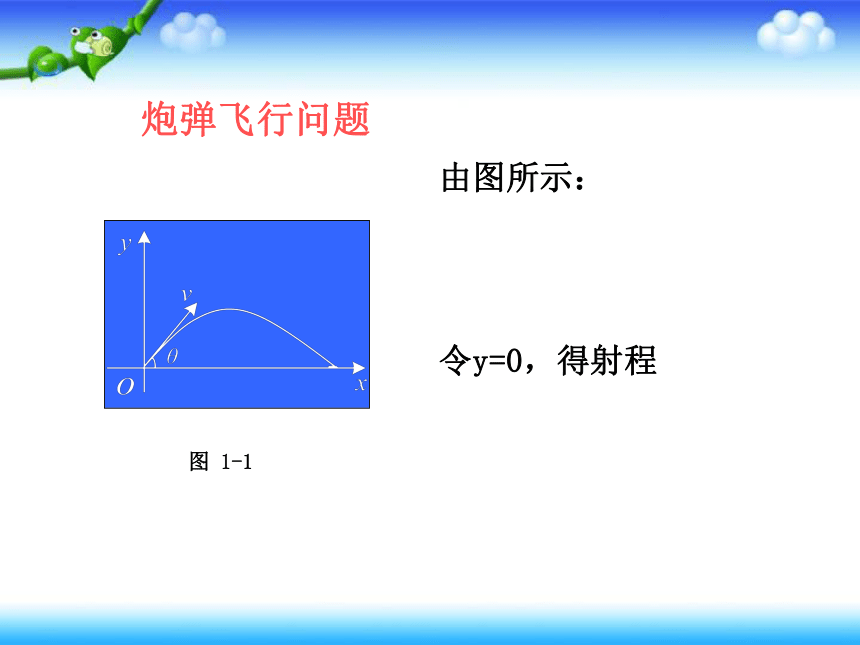
炮弹飞行问题
图 1-1
由图所示:
令y=0,得射程
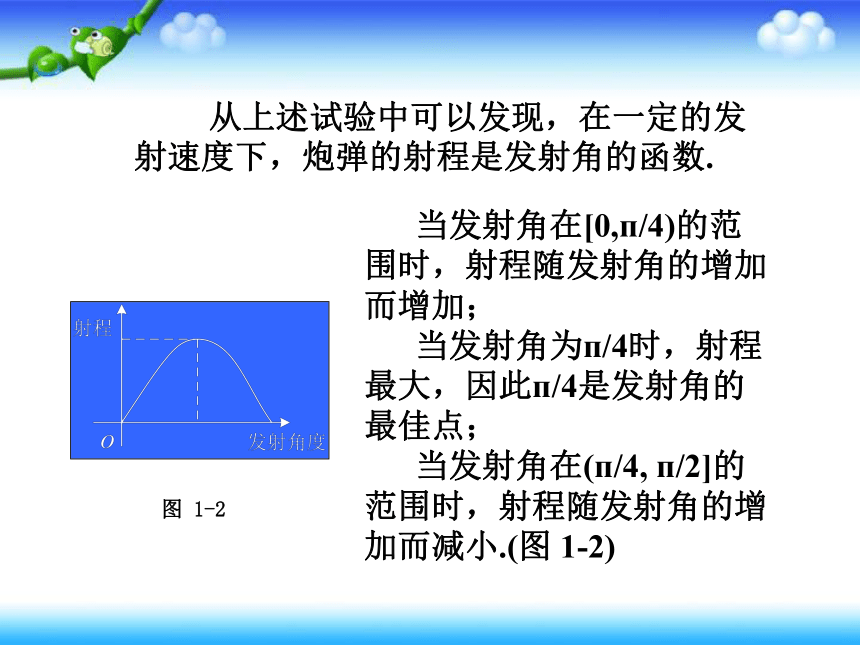
从上述试验中可以发现,在一定的发射速度下,炮弹的射程是发射角的函数.
当发射角在[0,п/4)的范围时,射程随发射角的增加而增加;
当发射角为п/4时,射程最大,因此п/4是发射角的最佳点;
当发射角在(п/4, п/2]的范围时,射程随发射角的增加而减小.(图 1-2)
图 1-2
从上述讨论中可以看出,在试验范围内有一个最佳点,但当在试验范围内变化因素的取值比最佳点再大些或再小些时,试验效果都差,而且取值距离最佳点越远试验效果越差,我们就称这样的试验具有单峰性.
接下来,我们就对单峰函数进行进一步的讲解……
第二节 单峰函数
教学目标
1. 知识与技能
(1)结合例子说明并掌握单峰函数、单因素问题、目标函数等概念.
(2)能够写出单因素问题下某区间内的目标函数.
(3)分析并掌握单峰函数中最佳点与好点和差点之间的关系.
2.过程与方法
(1)通过实例引入单峰函数,通过分析实例,指导学生观察分析,总结归纳.
(2)学生积极思考认真比较,理解单峰函数的定义,学会在单因素问题的条件下写出目标函数.
(3)学生在教师的指导下,通过实例,学会分析最佳点与好点和差点之间的关系.
3.情感态度与价值观
(1)通过学生之间的讨论、交流与协作探究,培养学生之间的团队合作精神.
(2)让学生在探究过程中体验解决问题的成功喜悦,增进学生学习的情感.
(3)学生在自主探究式的学习中,增强自己的创新能力,锻炼自己的思维分析能力.
教学重难点
重点
(1) 理解并掌握单峰函数的定义.
(2) 能够写出在单因素问题条件下某区间的目标函数.
(3) 掌握单峰函数中最佳点与好点和差点之间的关系.
(1)能够在实际问题中分析并且判断单峰函数.
(2)能够举例说明生活中遇到的具有单峰性质的现象.
观察
难点
想一想
根据前面的介绍,究竟什么是单峰函数呢?
单峰函数的定义
单峰函数的定义中注意的两个要点:
(1)f(x)在[a,b]上只有唯一的最大(小)值点C;
(2)f(x)在[a,C]上递增(减),在[C,b]上递减(增).例如,图1-3中的f(x)函数就是单峰函数.
图 1-3
“我们规定,区间[a,b]上的单调(递增或递减)函数也是单峰函数.” 这样的函数的最大(最小)值点是区间端点.
讨论
既然同学们已经了解了单峰函数的定义,那就讨论一下那些现象具有单峰性质呢?
单因素问题
在上述炮弹发射的试验中,我们把影响炮弹射程的物理量均称为因素.例如:发射角、初速度、空气阻力等.
但由于全面考虑试验中各种因素往往非常困难,我们经常忽略某些影响较小的因素,而把注意力集中在某个因素上面.例如:在炮弹发射的试验中,我们只考虑发射角这个因素,而忽略其他因素的影响.
因此,我们把只考虑试验过程中的一个因素对试验结果的影响的问题称为单因素问题.
总结
在单因素问题中,试验结果可以表示为一个一元函数f(x)(不一定要写出真正表达式),自变量x就是要考虑的影响试验结果的因素,定义域就是试验中因素x的变化范围[a,b](或在不考虑端点时写成(a,b)),这个函数就称为目标函数.
在分析完单因素问题之后,接下来的任务就是要选择某种方法来安排试验点(简称试点),我们要通过试验找出最佳点,使试验的结果(目标)最好.
介绍完试点之后呢,接下来,我们要学习好点和差点.
究竟什么是好点?什么又是差点呢?
好点与差点
设x1与x2是因素范围[a,b]内的任意两个试点,c点为最佳点,并把两个试点中效果较好的点称为好点,效果较差的点称为差点.
(1)
(2)
图 1-4
结论:
由图可以发现:
若目标函数为单峰函数,则最佳点与好点必在差点的同侧.
于是,如果我们以差点为分界点,把因素分为分成两部分,并称好点所在的部分为存优范围.
对于上述结论,我们应该怎样证明呢?
想一想
下面我们就针对单峰函数f(x)的上凸情形进行证明:
设点c为[a,b]上的单峰函数f(x)的最大值点,m,n在[a,b]的区间范围内,且f(m)>f(n).因为f(x)在[a,c]递增,在[c,b]递减.
(1) 设n属于[a,c],
因为m,n属于[a,b]且f(m)>f(n),
所以m不属于[a,n],即m属于[n,b].
因为n属于[a,c],
所以c属于[n,b].
因此,点m,c在点n的右侧.
(2)设n属于[c,b].
因为m,n属于[a,b]且f(m)>f(n),
所以m不属于[n,b],即m属于[a,n].
因为n属于[c,b],所以c属于[a,n].
因此,点m,n在点n的左侧.
由(1),(2)可知,点m,c始终在点n的同侧.
以上则为对上述结论的证明,请同学们加以理解……
课堂小结
单峰函数
(1)f(x)在[a,b]上只有唯一的最大(小)值点C;
(2)f(x)在[a,C]上递增(减),在[C,b]上递减(增).
单因素问题
我们把只考虑试验过程中的一个因素对试验结果的影响的问题称为单因素问题.
好点与差点
设x1与x2是因素范围[a,b]内的任意两个试点,c点为最佳点,并把两个试点中效果较好的点称为好点,效果较差的点称为差点.
最佳点、好点、差点
若目标函数为单峰函数,则最佳点与好点必在差点的同侧.
存优范围
我们以差点为分界点,把因素分为分成两部分,并称好点所在的部分为存优范围.
课堂练习
1.单峰函数的要点是什么?
答:(1)f(x)在[a,b]上只有唯一的最大(小)值点C;
(2)f(x)在[a,C]上递增(减),在[C,b]上递减(增).
2.判断下列函数在区间[-2,2]上那些是单峰函数:
(1) y=x2+5x-6;
(2) y=x2-4;
(3) y=x2-6x-8;
(4) y=x2+4x-12;
答:(2)、(4)
大
家
谈
在现实生活中遇到过哪些具有单峰性质的现象呢?
讨论
一.了解并掌握优选法的概念.
二.学会查找最佳点的方法.
三.学会如何利用优选法解决优选问题.
知识回顾
记忆
新课导入
在军事训练中,经常要考虑发射角度多大时炮弹的射程情况.
下面,我们就以一实际炮弹射程问题进行进一步学习……
炮弹飞行问题
图 1-1
由图所示:
令y=0,得射程
从上述试验中可以发现,在一定的发射速度下,炮弹的射程是发射角的函数.
当发射角在[0,п/4)的范围时,射程随发射角的增加而增加;
当发射角为п/4时,射程最大,因此п/4是发射角的最佳点;
当发射角在(п/4, п/2]的范围时,射程随发射角的增加而减小.(图 1-2)
图 1-2
从上述讨论中可以看出,在试验范围内有一个最佳点,但当在试验范围内变化因素的取值比最佳点再大些或再小些时,试验效果都差,而且取值距离最佳点越远试验效果越差,我们就称这样的试验具有单峰性.
接下来,我们就对单峰函数进行进一步的讲解……
第二节 单峰函数
教学目标
1. 知识与技能
(1)结合例子说明并掌握单峰函数、单因素问题、目标函数等概念.
(2)能够写出单因素问题下某区间内的目标函数.
(3)分析并掌握单峰函数中最佳点与好点和差点之间的关系.
2.过程与方法
(1)通过实例引入单峰函数,通过分析实例,指导学生观察分析,总结归纳.
(2)学生积极思考认真比较,理解单峰函数的定义,学会在单因素问题的条件下写出目标函数.
(3)学生在教师的指导下,通过实例,学会分析最佳点与好点和差点之间的关系.
3.情感态度与价值观
(1)通过学生之间的讨论、交流与协作探究,培养学生之间的团队合作精神.
(2)让学生在探究过程中体验解决问题的成功喜悦,增进学生学习的情感.
(3)学生在自主探究式的学习中,增强自己的创新能力,锻炼自己的思维分析能力.
教学重难点
重点
(1) 理解并掌握单峰函数的定义.
(2) 能够写出在单因素问题条件下某区间的目标函数.
(3) 掌握单峰函数中最佳点与好点和差点之间的关系.
(1)能够在实际问题中分析并且判断单峰函数.
(2)能够举例说明生活中遇到的具有单峰性质的现象.
观察
难点
想一想
根据前面的介绍,究竟什么是单峰函数呢?
单峰函数的定义
单峰函数的定义中注意的两个要点:
(1)f(x)在[a,b]上只有唯一的最大(小)值点C;
(2)f(x)在[a,C]上递增(减),在[C,b]上递减(增).例如,图1-3中的f(x)函数就是单峰函数.
图 1-3
“我们规定,区间[a,b]上的单调(递增或递减)函数也是单峰函数.” 这样的函数的最大(最小)值点是区间端点.
讨论
既然同学们已经了解了单峰函数的定义,那就讨论一下那些现象具有单峰性质呢?
单因素问题
在上述炮弹发射的试验中,我们把影响炮弹射程的物理量均称为因素.例如:发射角、初速度、空气阻力等.
但由于全面考虑试验中各种因素往往非常困难,我们经常忽略某些影响较小的因素,而把注意力集中在某个因素上面.例如:在炮弹发射的试验中,我们只考虑发射角这个因素,而忽略其他因素的影响.
因此,我们把只考虑试验过程中的一个因素对试验结果的影响的问题称为单因素问题.
总结
在单因素问题中,试验结果可以表示为一个一元函数f(x)(不一定要写出真正表达式),自变量x就是要考虑的影响试验结果的因素,定义域就是试验中因素x的变化范围[a,b](或在不考虑端点时写成(a,b)),这个函数就称为目标函数.
在分析完单因素问题之后,接下来的任务就是要选择某种方法来安排试验点(简称试点),我们要通过试验找出最佳点,使试验的结果(目标)最好.
介绍完试点之后呢,接下来,我们要学习好点和差点.
究竟什么是好点?什么又是差点呢?
好点与差点
设x1与x2是因素范围[a,b]内的任意两个试点,c点为最佳点,并把两个试点中效果较好的点称为好点,效果较差的点称为差点.
(1)
(2)
图 1-4
结论:
由图可以发现:
若目标函数为单峰函数,则最佳点与好点必在差点的同侧.
于是,如果我们以差点为分界点,把因素分为分成两部分,并称好点所在的部分为存优范围.
对于上述结论,我们应该怎样证明呢?
想一想
下面我们就针对单峰函数f(x)的上凸情形进行证明:
设点c为[a,b]上的单峰函数f(x)的最大值点,m,n在[a,b]的区间范围内,且f(m)>f(n).因为f(x)在[a,c]递增,在[c,b]递减.
(1) 设n属于[a,c],
因为m,n属于[a,b]且f(m)>f(n),
所以m不属于[a,n],即m属于[n,b].
因为n属于[a,c],
所以c属于[n,b].
因此,点m,c在点n的右侧.
(2)设n属于[c,b].
因为m,n属于[a,b]且f(m)>f(n),
所以m不属于[n,b],即m属于[a,n].
因为n属于[c,b],所以c属于[a,n].
因此,点m,n在点n的左侧.
由(1),(2)可知,点m,c始终在点n的同侧.
以上则为对上述结论的证明,请同学们加以理解……
课堂小结
单峰函数
(1)f(x)在[a,b]上只有唯一的最大(小)值点C;
(2)f(x)在[a,C]上递增(减),在[C,b]上递减(增).
单因素问题
我们把只考虑试验过程中的一个因素对试验结果的影响的问题称为单因素问题.
好点与差点
设x1与x2是因素范围[a,b]内的任意两个试点,c点为最佳点,并把两个试点中效果较好的点称为好点,效果较差的点称为差点.
最佳点、好点、差点
若目标函数为单峰函数,则最佳点与好点必在差点的同侧.
存优范围
我们以差点为分界点,把因素分为分成两部分,并称好点所在的部分为存优范围.
课堂练习
1.单峰函数的要点是什么?
答:(1)f(x)在[a,b]上只有唯一的最大(小)值点C;
(2)f(x)在[a,C]上递增(减),在[C,b]上递减(增).
2.判断下列函数在区间[-2,2]上那些是单峰函数:
(1) y=x2+5x-6;
(2) y=x2-4;
(3) y=x2-6x-8;
(4) y=x2+4x-12;
答:(2)、(4)
大
家
谈
在现实生活中遇到过哪些具有单峰性质的现象呢?
讨论
