人教A版高中数学选修4-7 第二讲 实验设计初步 二 正交试验的应用 上课课件(共31张PPT)
文档属性
| 名称 | 人教A版高中数学选修4-7 第二讲 实验设计初步 二 正交试验的应用 上课课件(共31张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 949.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-18 11:26:43 | ||
图片预览









文档简介
(共31张PPT)
知识回顾
正交表介绍
正交试验设计
正交试验应用
确定试验的因素和水平
正交表特性
选择合适的正交表
做表头设计
确定试验方案
试验结果分析,选出最佳组合
新课导入
想一想···
从教材中的案例1可以发现,用正交表安排试验只做了因素和水平所有组合中的一部分,那么只做部分试验能找出所有可能组合中的最好点吗?
提示:
从正交表的特性分析试验
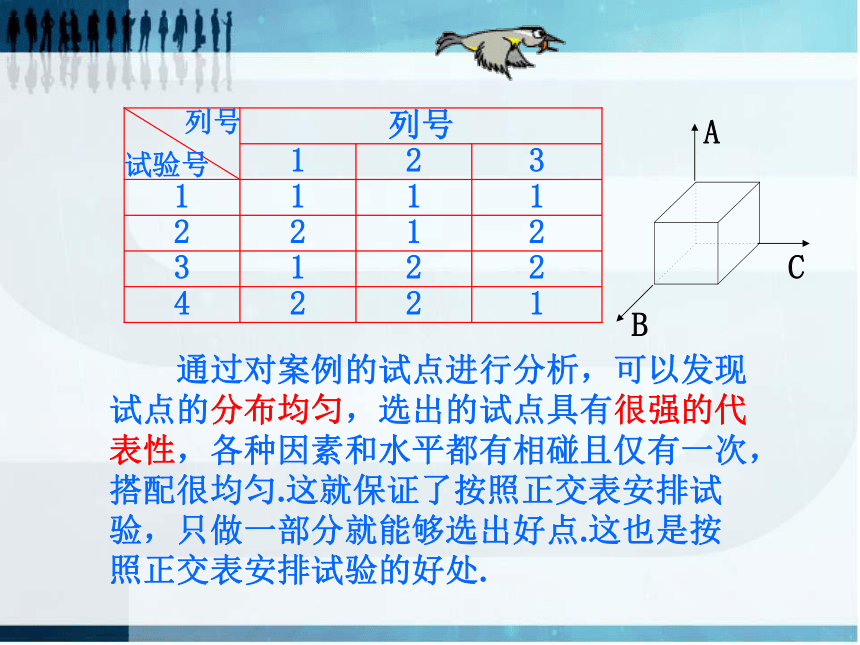
通过对案例的试点进行分析,可以发现试点的分布均匀,选出的试点具有很强的代表性,各种因素和水平都有相碰且仅有一次,搭配很均匀.这就保证了按照正交表安排试验,只做一部分就能够选出好点.这也是按照正交表安排试验的好处.
1
2
2
4
2
2
1
3
2
1
2
2
1
1
1
1
3
2
1
列号
列号
试验号
A
B
C
大
家
谈
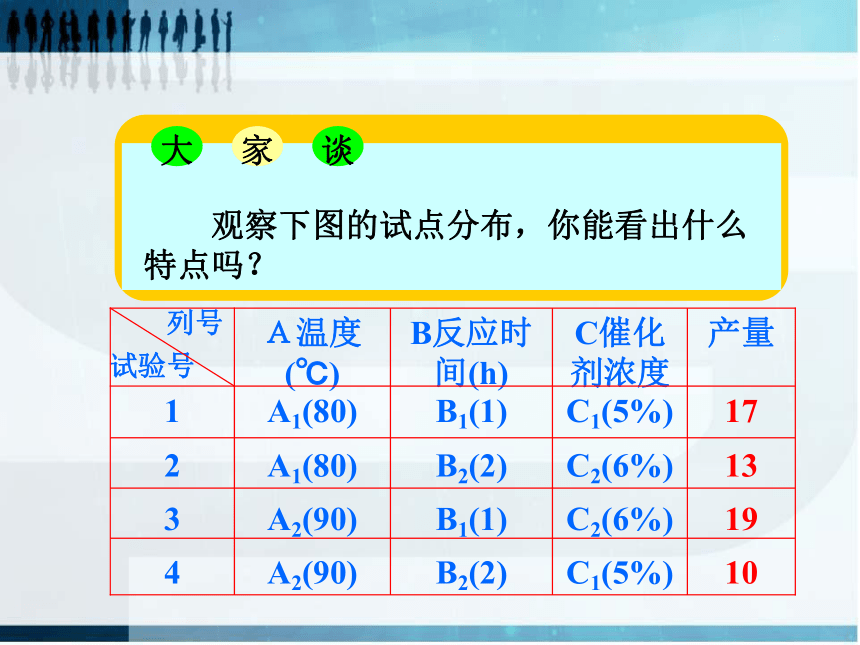
观察下图的试点分布,你能看出什么特点吗?
列号
试验号
10
C1(5%)
B2(2)
A2(90)
4
19
C2(6%)
B1(1)
A2(90)
3
13
C2(6%)
B2(2)
A1(80)
2
17
C1(5%)
B1(1)
A1(80)
1
产量
C催化剂浓度
B反应时间(h)
A温度
(℃)
总结
选出试点具有很强的代表性,各种因素和其他水平有相碰且仅有一次,可以归结出正交表的两条特性:
1.均衡分散性
2.整齐可比性
2.2 正交试验的应用
教学目标
知识与能力
过程与方法
1.了解正交表的结构特点.
2.了解正交试验设计试验的基本过程.
3.体会优选的思想.
通过对现实中具体实例的分析,熟悉正交表的结构特点,学习用正交表设计试验的基本过程.
情感态度与价值观
通过对现实问题的分析,能够对正交表的特性有比较感性的认识,提高学生对现实生活中问题的观察与分析能力.体会正交表在设计试验中具有的重要作用以及优选的思想.
教学重难点
重点
难点
了解用正交试验设计方法解决简单问题的过程,概括正交表的基本特性,体会优选思想.
了解正交试验的思想和方法,概括正交表中试点均匀分布的特性.正确应用正交表.
本节导航
一.通过案例提出如何只做部分试验找出最好点
二.观察试点分布,寻找试点分布规律
三.辨析正交表的特点
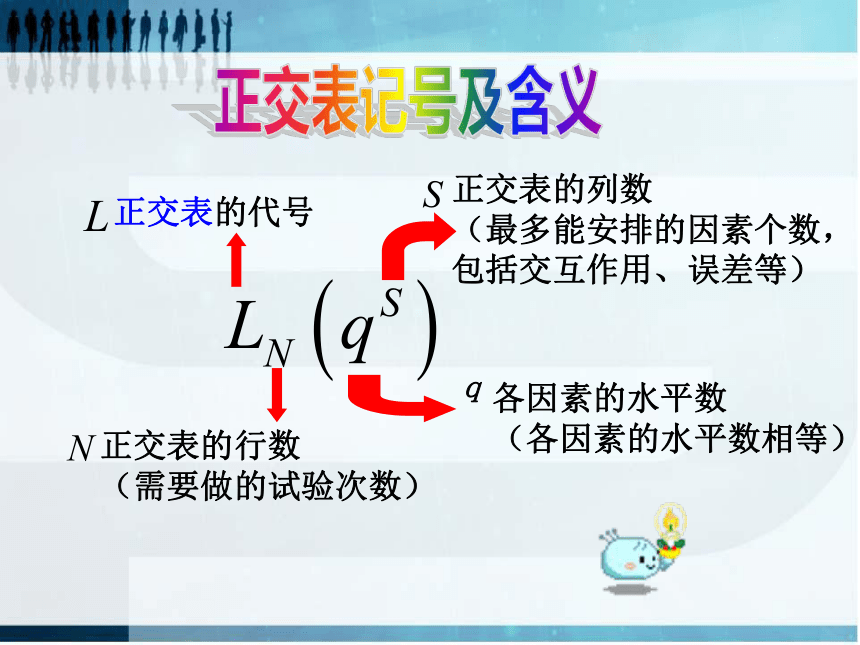
正交表的列数
(最多能安排的因素个数,
包括交互作用、误差等)
正交表的行数
(需要做的试验次数)
各因素的水平数
(各因素的水平数相等)
q
正交表的代号
正交表记号及含义
想一想······
表示
表示各因素的水平数为2,做8次试验,最多考虑7个因素(含交互作用)的正交表.
?
案例1
为了解决花菜留种问题,以进一步提高花菜种子的产量和质量,科技人员考察了浇水、施肥、病害防治和移入温室时间对花菜留种的影响,进行了四个因素各两个水平的正交试验,各因素及其水平如下表:
我们学种花菜···
因素 水平1 水平2
A:浇水次数 不干死为原则,整个生长期只浇水1~2次 根据生长需水量和自然条件浇水,但不过湿
B:喷药次数 发现病害即喷药 每半月喷一次
C:施肥次数 开花期施硫酸铵 进室发根期、抽薹期、开花期和结果期各施肥一次
D:进室时间 11月初 11月15日
【解析】
第一步:选择适当的正交表
这是一个四因素两水平的正交试验及分析问题.
因此要选择LN(2S)型的表,且不考虑交互作用时,S≥4,而L8(27)是满足条件的最小的正交表,所以选用正交表 L8(27).
若考虑A与B、A与C的交互作用
则S≥6, L8(27)仍然是满足条件的最小的正交表,所以还可以选用正交表L8(27).
其中:
N由 确定.
是可求出的,而 是未知的,
当不考虑交互作用时:可取
故 N 不是唯一的.
所以一般地,由
确定 N,
所以一般地,有
如三因素四水平 43 的正交试验至少应安排
3(4-1)+1=10次以上的试验.
如三因素四水平 43 并包括第一、二个因素的交互作用的正交试验至少应安排的试验次数为3(4-1)+(4-1)(4-1)+1=19.
又如安排43×23的混合水平的正交试验至少应安排3(4-1)+3(2-1)+1=13次以上的试验.
若再加上包括第一、五个因素的交互作用的正交试验则至少应安排的试验次数为
3(4-1)+3(2-1)+(4-1)(2-1)+1=16.
第二步 表头设计——查交互作用表
表示位于第二、第四列的两因素的交互作用要放于第六列.
注意:主效应因素尽量不放交互列.如A、B因素已放C1、C2列,则C 因素就不放C3列.
如P190 L8(27)的交互作用表
列号 1 2 3 4 5 6 7
1 (1) 3 2 5 4 7 6
2 (2) 1 6 7 4 5
3 (3) 7 6 5 4
4 (4) 1 2 3
5 (5) 3 2
6 (6) 1
列号 1 2 3 4 5 6 7
因子
考虑交互作用A?B和A?C,则例1的表头可设计为:
按正交表 得试验方案:
只需将各列中的数字“1”、“2”分别理解为所填因素在试验中的水平数,每一行就是一个试验方案.
375
275
250
200
425
425
325
350
产量
2
1
1
2
1
2
2
1
7
D
1
2
2
1
1
2
2
1
6
1
2
1
2
2
1
2
1
5
AXC
2
1
2
2
8
1
1
2
2
7
2
2
1
2
6
1
2
1
2
5
2
2
2
1
4
1
2
2
1
3
2
1
1
1
2
1
1
1
1
1
4
3
2
1
C
AXB
B
A
列号
水平
试验号
第三步 按所选定的正交试验方案组织试验,记录试验结果;
第四步 分析正交试验结果
直观分析(极差分析)
(1)计算极差,确定因素的主次顺序
第j列的极差
或
极差越大,说明这个因素的水平改变对试验结果的影响越大,极差最大的那个因素,就是最主要的因素.
对例1来说,各因素的主次顺序为
通过对案例的试点进行分析,可以发现试点的分布均匀,选出的试点具有很强的代表性,各种因素和水平都有相碰且仅有一次,搭配很均匀.这就保证了按照正交表安排试验,只做一部分就能够选出好点.这也是按照正交表安排试验的好处.
同学们,对于种花菜,你了解了吗?
你知道怎样解决花菜留种问题了吗?
有机会多多观察哦······
课堂小结
设计正交试验表的基本准则:
1、正交表中任意一列中,不同的数字出现的次数相等;
表示:在试验安排中,所挑选出来的水平组合是均匀分布的(每个因素的各水平出现的次数相同)——均衡分散性.
2、正交表中任意两列,把同行的两个数字看成有序数对时,所有可能的数对出现的次数相同.
表示:任意两因素的各种水平的搭配在所选试验中出现的次数相等——整齐可比性.
课堂练习
如果一个3因素3水平的正交试验结果如下表:
A B C 4 实验结果
1 A1 B1 C1 1 45
2 A1 B2 C2 2 53
3 A1 B3 C3 3 61
4 A2 B1 C1 3 55
5 A2 B2 C3 1 57
6 A2 B3 C1 2 48
7 A3 B1 C3 2 64
8 A3 B2 C1 3 52
9 A3 B3 C1 1 58
完成下表,求使得试验结果最优(数值最大)的因素组合,并找出影响试验结果的最主要因素.
Rq
k2q=1/3K2q
k3q=1/3K3q
k1q=1/3K1q
Rq
k2q=1/3K2q
k3q=1/3K3q
k1q=1/3K1q
61
53
54
8
58
57
57
1
7
60
58
53
从上表可以看出,影响结果最显著的因素是A,其次是因素C,因素B的影响最小.最优组合为
(A1,B1,C3)
解析:
2.考察表所列的对胶鞋弯曲性能有影响的3个因素和2个水平,请选取主要因素及较好的配方.
2.0
乙类炭黑
1.0
2
2.5
甲类炭黑
1.5
1
C
硫磺用量
B
炭黑品种
A
促进剂总量
因素
水平
答案:(A1,B1,C2)
3.某农场希望知道某个玉米品种的高产栽培条件,研究人员选择了3个试验因素:种植密度、施化肥量、施化肥时间,每个试验因素选3个水平,如表所示:
按3:5分2次施完
2800
30
3
一次施完
3200
40
2
按1:2:1分3次施完
3700
50
1
C
施化肥时间
B种植密度
(株/亩)
A施化肥量
(kg/亩)
因素
水平
最好的试验结果是什么?
提示:
1.找出适合实验要求的正交表
2.画产量和因素的关系图
3.从表中分析及验证
答案:
验证试验现实,(A21,B1,C3)为最好试验结果.水平搭配的试验结果为亩产量493.0kg.
知识回顾
正交表介绍
正交试验设计
正交试验应用
确定试验的因素和水平
正交表特性
选择合适的正交表
做表头设计
确定试验方案
试验结果分析,选出最佳组合
新课导入
想一想···
从教材中的案例1可以发现,用正交表安排试验只做了因素和水平所有组合中的一部分,那么只做部分试验能找出所有可能组合中的最好点吗?
提示:
从正交表的特性分析试验
通过对案例的试点进行分析,可以发现试点的分布均匀,选出的试点具有很强的代表性,各种因素和水平都有相碰且仅有一次,搭配很均匀.这就保证了按照正交表安排试验,只做一部分就能够选出好点.这也是按照正交表安排试验的好处.
1
2
2
4
2
2
1
3
2
1
2
2
1
1
1
1
3
2
1
列号
列号
试验号
A
B
C
大
家
谈
观察下图的试点分布,你能看出什么特点吗?
列号
试验号
10
C1(5%)
B2(2)
A2(90)
4
19
C2(6%)
B1(1)
A2(90)
3
13
C2(6%)
B2(2)
A1(80)
2
17
C1(5%)
B1(1)
A1(80)
1
产量
C催化剂浓度
B反应时间(h)
A温度
(℃)
总结
选出试点具有很强的代表性,各种因素和其他水平有相碰且仅有一次,可以归结出正交表的两条特性:
1.均衡分散性
2.整齐可比性
2.2 正交试验的应用
教学目标
知识与能力
过程与方法
1.了解正交表的结构特点.
2.了解正交试验设计试验的基本过程.
3.体会优选的思想.
通过对现实中具体实例的分析,熟悉正交表的结构特点,学习用正交表设计试验的基本过程.
情感态度与价值观
通过对现实问题的分析,能够对正交表的特性有比较感性的认识,提高学生对现实生活中问题的观察与分析能力.体会正交表在设计试验中具有的重要作用以及优选的思想.
教学重难点
重点
难点
了解用正交试验设计方法解决简单问题的过程,概括正交表的基本特性,体会优选思想.
了解正交试验的思想和方法,概括正交表中试点均匀分布的特性.正确应用正交表.
本节导航
一.通过案例提出如何只做部分试验找出最好点
二.观察试点分布,寻找试点分布规律
三.辨析正交表的特点
正交表的列数
(最多能安排的因素个数,
包括交互作用、误差等)
正交表的行数
(需要做的试验次数)
各因素的水平数
(各因素的水平数相等)
q
正交表的代号
正交表记号及含义
想一想······
表示
表示各因素的水平数为2,做8次试验,最多考虑7个因素(含交互作用)的正交表.
?
案例1
为了解决花菜留种问题,以进一步提高花菜种子的产量和质量,科技人员考察了浇水、施肥、病害防治和移入温室时间对花菜留种的影响,进行了四个因素各两个水平的正交试验,各因素及其水平如下表:
我们学种花菜···
因素 水平1 水平2
A:浇水次数 不干死为原则,整个生长期只浇水1~2次 根据生长需水量和自然条件浇水,但不过湿
B:喷药次数 发现病害即喷药 每半月喷一次
C:施肥次数 开花期施硫酸铵 进室发根期、抽薹期、开花期和结果期各施肥一次
D:进室时间 11月初 11月15日
【解析】
第一步:选择适当的正交表
这是一个四因素两水平的正交试验及分析问题.
因此要选择LN(2S)型的表,且不考虑交互作用时,S≥4,而L8(27)是满足条件的最小的正交表,所以选用正交表 L8(27).
若考虑A与B、A与C的交互作用
则S≥6, L8(27)仍然是满足条件的最小的正交表,所以还可以选用正交表L8(27).
其中:
N由 确定.
是可求出的,而 是未知的,
当不考虑交互作用时:可取
故 N 不是唯一的.
所以一般地,由
确定 N,
所以一般地,有
如三因素四水平 43 的正交试验至少应安排
3(4-1)+1=10次以上的试验.
如三因素四水平 43 并包括第一、二个因素的交互作用的正交试验至少应安排的试验次数为3(4-1)+(4-1)(4-1)+1=19.
又如安排43×23的混合水平的正交试验至少应安排3(4-1)+3(2-1)+1=13次以上的试验.
若再加上包括第一、五个因素的交互作用的正交试验则至少应安排的试验次数为
3(4-1)+3(2-1)+(4-1)(2-1)+1=16.
第二步 表头设计——查交互作用表
表示位于第二、第四列的两因素的交互作用要放于第六列.
注意:主效应因素尽量不放交互列.如A、B因素已放C1、C2列,则C 因素就不放C3列.
如P190 L8(27)的交互作用表
列号 1 2 3 4 5 6 7
1 (1) 3 2 5 4 7 6
2 (2) 1 6 7 4 5
3 (3) 7 6 5 4
4 (4) 1 2 3
5 (5) 3 2
6 (6) 1
列号 1 2 3 4 5 6 7
因子
考虑交互作用A?B和A?C,则例1的表头可设计为:
按正交表 得试验方案:
只需将各列中的数字“1”、“2”分别理解为所填因素在试验中的水平数,每一行就是一个试验方案.
375
275
250
200
425
425
325
350
产量
2
1
1
2
1
2
2
1
7
D
1
2
2
1
1
2
2
1
6
1
2
1
2
2
1
2
1
5
AXC
2
1
2
2
8
1
1
2
2
7
2
2
1
2
6
1
2
1
2
5
2
2
2
1
4
1
2
2
1
3
2
1
1
1
2
1
1
1
1
1
4
3
2
1
C
AXB
B
A
列号
水平
试验号
第三步 按所选定的正交试验方案组织试验,记录试验结果;
第四步 分析正交试验结果
直观分析(极差分析)
(1)计算极差,确定因素的主次顺序
第j列的极差
或
极差越大,说明这个因素的水平改变对试验结果的影响越大,极差最大的那个因素,就是最主要的因素.
对例1来说,各因素的主次顺序为
通过对案例的试点进行分析,可以发现试点的分布均匀,选出的试点具有很强的代表性,各种因素和水平都有相碰且仅有一次,搭配很均匀.这就保证了按照正交表安排试验,只做一部分就能够选出好点.这也是按照正交表安排试验的好处.
同学们,对于种花菜,你了解了吗?
你知道怎样解决花菜留种问题了吗?
有机会多多观察哦······
课堂小结
设计正交试验表的基本准则:
1、正交表中任意一列中,不同的数字出现的次数相等;
表示:在试验安排中,所挑选出来的水平组合是均匀分布的(每个因素的各水平出现的次数相同)——均衡分散性.
2、正交表中任意两列,把同行的两个数字看成有序数对时,所有可能的数对出现的次数相同.
表示:任意两因素的各种水平的搭配在所选试验中出现的次数相等——整齐可比性.
课堂练习
如果一个3因素3水平的正交试验结果如下表:
A B C 4 实验结果
1 A1 B1 C1 1 45
2 A1 B2 C2 2 53
3 A1 B3 C3 3 61
4 A2 B1 C1 3 55
5 A2 B2 C3 1 57
6 A2 B3 C1 2 48
7 A3 B1 C3 2 64
8 A3 B2 C1 3 52
9 A3 B3 C1 1 58
完成下表,求使得试验结果最优(数值最大)的因素组合,并找出影响试验结果的最主要因素.
Rq
k2q=1/3K2q
k3q=1/3K3q
k1q=1/3K1q
Rq
k2q=1/3K2q
k3q=1/3K3q
k1q=1/3K1q
61
53
54
8
58
57
57
1
7
60
58
53
从上表可以看出,影响结果最显著的因素是A,其次是因素C,因素B的影响最小.最优组合为
(A1,B1,C3)
解析:
2.考察表所列的对胶鞋弯曲性能有影响的3个因素和2个水平,请选取主要因素及较好的配方.
2.0
乙类炭黑
1.0
2
2.5
甲类炭黑
1.5
1
C
硫磺用量
B
炭黑品种
A
促进剂总量
因素
水平
答案:(A1,B1,C2)
3.某农场希望知道某个玉米品种的高产栽培条件,研究人员选择了3个试验因素:种植密度、施化肥量、施化肥时间,每个试验因素选3个水平,如表所示:
按3:5分2次施完
2800
30
3
一次施完
3200
40
2
按1:2:1分3次施完
3700
50
1
C
施化肥时间
B种植密度
(株/亩)
A施化肥量
(kg/亩)
因素
水平
最好的试验结果是什么?
提示:
1.找出适合实验要求的正交表
2.画产量和因素的关系图
3.从表中分析及验证
答案:
验证试验现实,(A21,B1,C3)为最好试验结果.水平搭配的试验结果为亩产量493.0kg.
