2020鲁教版五四制七上数学1.1认识三角形第2课时课件(24张ppt)
文档属性
| 名称 | 2020鲁教版五四制七上数学1.1认识三角形第2课时课件(24张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 00:00:00 | ||
图片预览





文档简介
课件24张PPT。1 认识三角形
第2课时1.了解三角形的中线、角平分线、高的概念.
2.知道三角形的中线、角平分线、高所在的直线交于一点.
3.会利用三角形的中线、角平分线、高解决实际问题,进一步提高学生的空间想象能力和语言表述能力.⒈ 判断下列长度的三条线段a,b,c能否组成三角形.
⑴ a=1 cm,b=2 cm,c=3 cm;
⑵ a=10 cm,b=6 cm,c=3 cm;
⑶ a=2 cm,b=10 cm,c=11 cm;
⑷ a=1.1 cm;b=8.2 cm,c=9.31 cm.
⒉ 三角形的三个内角的和等于 度.180√⒊ 直角三角形的两个锐角 .
⒋ 一个三角形的三个内角中( )
(A)至少有一个角等于90°
(B)至少有一个角大于90°
(C)可能只有一个角小于90°
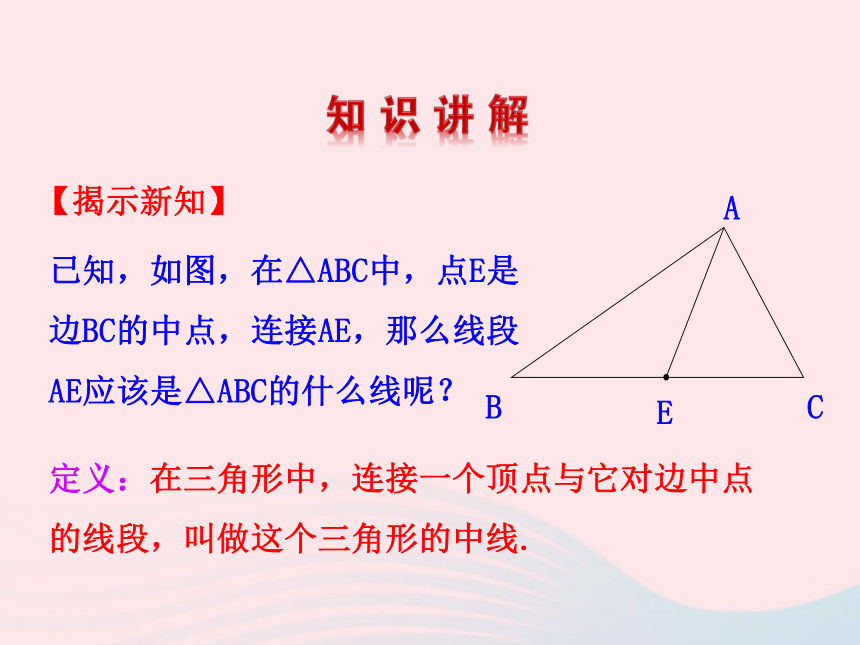
(D)不可能都小于60°互余D⒌ 如图,线段DG,EM,FN两两相交于B,C,A三点,则
∠D+∠E+∠F+∠G+∠M+∠N的度数是( )
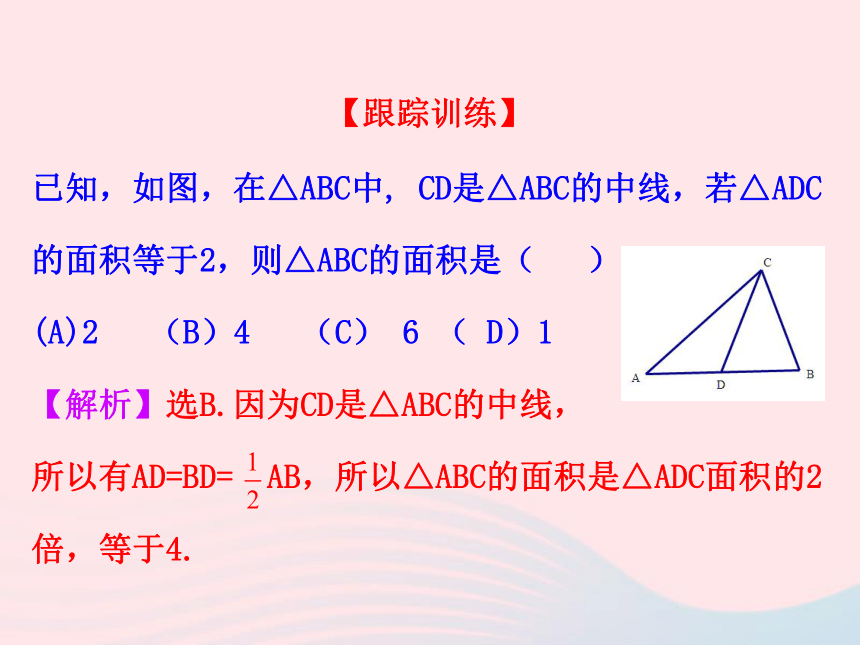
(A)90° (B)180° (C)270° (D)360°D已知,如图,在△ABC中,点E是边BC的中点,连接AE,那么线段AE应该是△ABC的什么线呢?定义:在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线.【揭示新知】(1)在纸上画一个锐角三角形,并画出这个三角形的三条中线,它们有怎样的位置关系?
(2)直角三角形、钝角三角形的三条中线是否也有同样的位置关系?
折一折,画一画,并与同伴进行交流.三角形的三条中线交于一点,这点称为三角形的重心.【做一做】已知,如图,在△ABC中, CD是△ABC的中线,若△ADC的面积等于2,则△ABC的面积是( )
(A)2 (B)4 (C) 6 ( D)1
【解析】选B.因为CD是△ABC的中线,
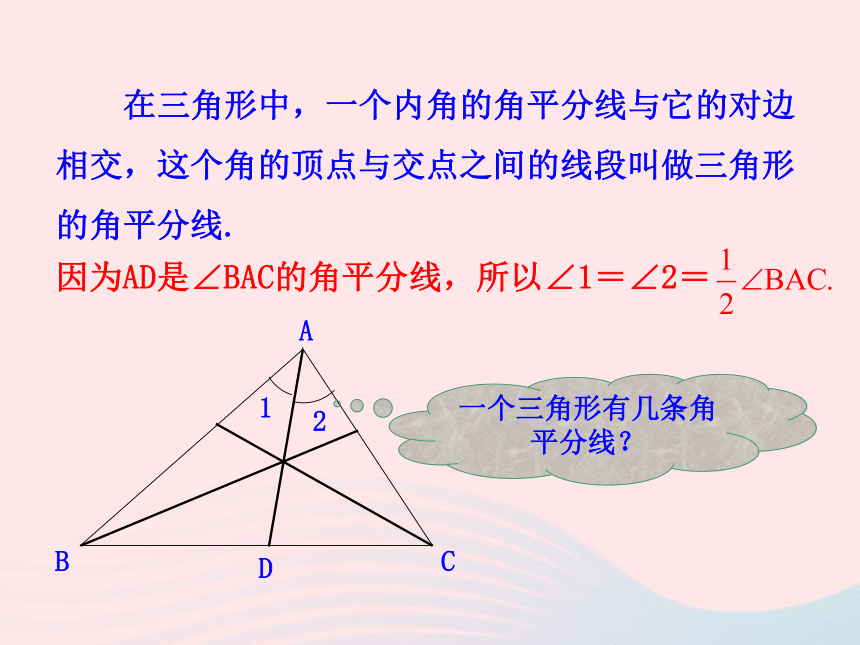
所以有AD=BD= AB,所以△ABC的面积是△ADC面积的2倍,等于4.【跟踪训练】 在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.D12因为AD是∠BAC的角平分线,所以∠1=∠2=一个三角形有几条角平分线? 每人准备锐角三角形、直角三角形、钝角三角形纸片各一个.
(1)你能分别画出这三个三角形的三条角平分线吗?
(2)你能通过折纸的方法得到它们吗?
(3)在每个三角形中,三条角平分线之间有怎样的位置关系?
将你的结果与同伴进行交流.三角形的三条角平分线交于一点.【做一做】你会“过一点画已知直线的垂线”吗?画法:过三角形的一个顶点,你能画出它的对边的垂线吗?BAC【做一做】A从三角形的一个顶点BC向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.如图, 线段AD是BC边上的高.任意画一个锐角三角形ABC,请你画出BC边上的高.【画一画】每人准备一个锐角三角形的纸片.
(1) 你能画出这个三角形的三条高吗?(3) 这三条高之间有怎样的位置关系?将你的结果与同伴进行交流.锐角三角形的三条高交于同一点.(2) 你能用折纸的办法得到它们吗?锐角三角形的三条高是在三角形的内部还是外部?锐角三角形的三条高都在三角形的内部.ABCDEF在纸上画出一个直角三角形.将你的结果与同伴进行交流.ABC(1) 画出直角三角形的三条高,直角边BC边上的高是 ;AB直角边AB边上的高是 ;CB(2)它们有怎样的位置关系?直角三角形的三条高交于直角顶点.D斜边AC边上的高是 .BD●(1) 钝角三角形的三条高交于一点吗?钝角三角形的三条高不相交于一点(2)它们所在的直线交于一点吗?将你的结果与同伴进行交流.钝角三角形的三条高所在直线交于一点O三角形的三条高所在直线交于一点因为AD是△ABC的高,D所以∠BDA=∠CDA=90°.三角形的高的表示法【揭示新知】如图,在△ABC中, ∠1=∠2,G为AD的中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法哪些是正确的,哪些是错误的.①AD是△ABE的角平分线 ( )②BE是△ABD边AD上的中线 ( )③BE是△ABC边AC上的中线 ( )④CH是△ACD边AD上的高 ( )三角形的高、中线与角平分线都是线段×××√【跟踪训练】2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )(A)锐角三角形 (B)直角三角形
(C)钝角三角形 (D)不确定1.下列图形,哪一个图形中AD是△ABC的高( )(A)(B)(C)(D)BDD3.如图所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC
翻折180°,使点B 落在点B′的位置,则线段AC具有的
性质( )
(A)是边BB′上的中线 (B)是边BB′上的高
(C)是∠BAB′的平分线 (D)以上三种性质合一4.如图所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
(A)DE是△BCD的中线
(B)BD是△ABC的中线
(C)AD=DC,BD=EC
(D)∠C的对边是DEC5.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高.填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°.CEBC∠CAD∠BAC∠AFC⒈ 三角形的角平分线、中线、高线的定义.
⒉ 三角形的三条角平分线交于一点,三条中线交于一点,三条高所在的直线交于一点. 通过本课时的学习,需要我们掌握:人生如登山,往上走,即使一小步也有新高度.
第2课时1.了解三角形的中线、角平分线、高的概念.
2.知道三角形的中线、角平分线、高所在的直线交于一点.
3.会利用三角形的中线、角平分线、高解决实际问题,进一步提高学生的空间想象能力和语言表述能力.⒈ 判断下列长度的三条线段a,b,c能否组成三角形.
⑴ a=1 cm,b=2 cm,c=3 cm;
⑵ a=10 cm,b=6 cm,c=3 cm;
⑶ a=2 cm,b=10 cm,c=11 cm;
⑷ a=1.1 cm;b=8.2 cm,c=9.31 cm.
⒉ 三角形的三个内角的和等于 度.180√⒊ 直角三角形的两个锐角 .
⒋ 一个三角形的三个内角中( )
(A)至少有一个角等于90°
(B)至少有一个角大于90°
(C)可能只有一个角小于90°
(D)不可能都小于60°互余D⒌ 如图,线段DG,EM,FN两两相交于B,C,A三点,则
∠D+∠E+∠F+∠G+∠M+∠N的度数是( )
(A)90° (B)180° (C)270° (D)360°D已知,如图,在△ABC中,点E是边BC的中点,连接AE,那么线段AE应该是△ABC的什么线呢?定义:在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线.【揭示新知】(1)在纸上画一个锐角三角形,并画出这个三角形的三条中线,它们有怎样的位置关系?
(2)直角三角形、钝角三角形的三条中线是否也有同样的位置关系?
折一折,画一画,并与同伴进行交流.三角形的三条中线交于一点,这点称为三角形的重心.【做一做】已知,如图,在△ABC中, CD是△ABC的中线,若△ADC的面积等于2,则△ABC的面积是( )
(A)2 (B)4 (C) 6 ( D)1
【解析】选B.因为CD是△ABC的中线,
所以有AD=BD= AB,所以△ABC的面积是△ADC面积的2倍,等于4.【跟踪训练】 在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.D12因为AD是∠BAC的角平分线,所以∠1=∠2=一个三角形有几条角平分线? 每人准备锐角三角形、直角三角形、钝角三角形纸片各一个.
(1)你能分别画出这三个三角形的三条角平分线吗?
(2)你能通过折纸的方法得到它们吗?
(3)在每个三角形中,三条角平分线之间有怎样的位置关系?
将你的结果与同伴进行交流.三角形的三条角平分线交于一点.【做一做】你会“过一点画已知直线的垂线”吗?画法:过三角形的一个顶点,你能画出它的对边的垂线吗?BAC【做一做】A从三角形的一个顶点BC向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.如图, 线段AD是BC边上的高.任意画一个锐角三角形ABC,请你画出BC边上的高.【画一画】每人准备一个锐角三角形的纸片.
(1) 你能画出这个三角形的三条高吗?(3) 这三条高之间有怎样的位置关系?将你的结果与同伴进行交流.锐角三角形的三条高交于同一点.(2) 你能用折纸的办法得到它们吗?锐角三角形的三条高是在三角形的内部还是外部?锐角三角形的三条高都在三角形的内部.ABCDEF在纸上画出一个直角三角形.将你的结果与同伴进行交流.ABC(1) 画出直角三角形的三条高,直角边BC边上的高是 ;AB直角边AB边上的高是 ;CB(2)它们有怎样的位置关系?直角三角形的三条高交于直角顶点.D斜边AC边上的高是 .BD●(1) 钝角三角形的三条高交于一点吗?钝角三角形的三条高不相交于一点(2)它们所在的直线交于一点吗?将你的结果与同伴进行交流.钝角三角形的三条高所在直线交于一点O三角形的三条高所在直线交于一点因为AD是△ABC的高,D所以∠BDA=∠CDA=90°.三角形的高的表示法【揭示新知】如图,在△ABC中, ∠1=∠2,G为AD的中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法哪些是正确的,哪些是错误的.①AD是△ABE的角平分线 ( )②BE是△ABD边AD上的中线 ( )③BE是△ABC边AC上的中线 ( )④CH是△ACD边AD上的高 ( )三角形的高、中线与角平分线都是线段×××√【跟踪训练】2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )(A)锐角三角形 (B)直角三角形
(C)钝角三角形 (D)不确定1.下列图形,哪一个图形中AD是△ABC的高( )(A)(B)(C)(D)BDD3.如图所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC
翻折180°,使点B 落在点B′的位置,则线段AC具有的
性质( )
(A)是边BB′上的中线 (B)是边BB′上的高
(C)是∠BAB′的平分线 (D)以上三种性质合一4.如图所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
(A)DE是△BCD的中线
(B)BD是△ABC的中线
(C)AD=DC,BD=EC
(D)∠C的对边是DEC5.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高.填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°.CEBC∠CAD∠BAC∠AFC⒈ 三角形的角平分线、中线、高线的定义.
⒉ 三角形的三条角平分线交于一点,三条中线交于一点,三条高所在的直线交于一点. 通过本课时的学习,需要我们掌握:人生如登山,往上走,即使一小步也有新高度.
