2019年四川省成都市七中育才学校九年级数学上册 第1章 特殊平行四边形 复习(部分有答案)
文档属性
| 名称 | 2019年四川省成都市七中育才学校九年级数学上册 第1章 特殊平行四边形 复习(部分有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 00:00:00 | ||
图片预览


文档简介
成都市七中育才学校初2019届九年级数学上册 第1章 特殊平行四边形 复习
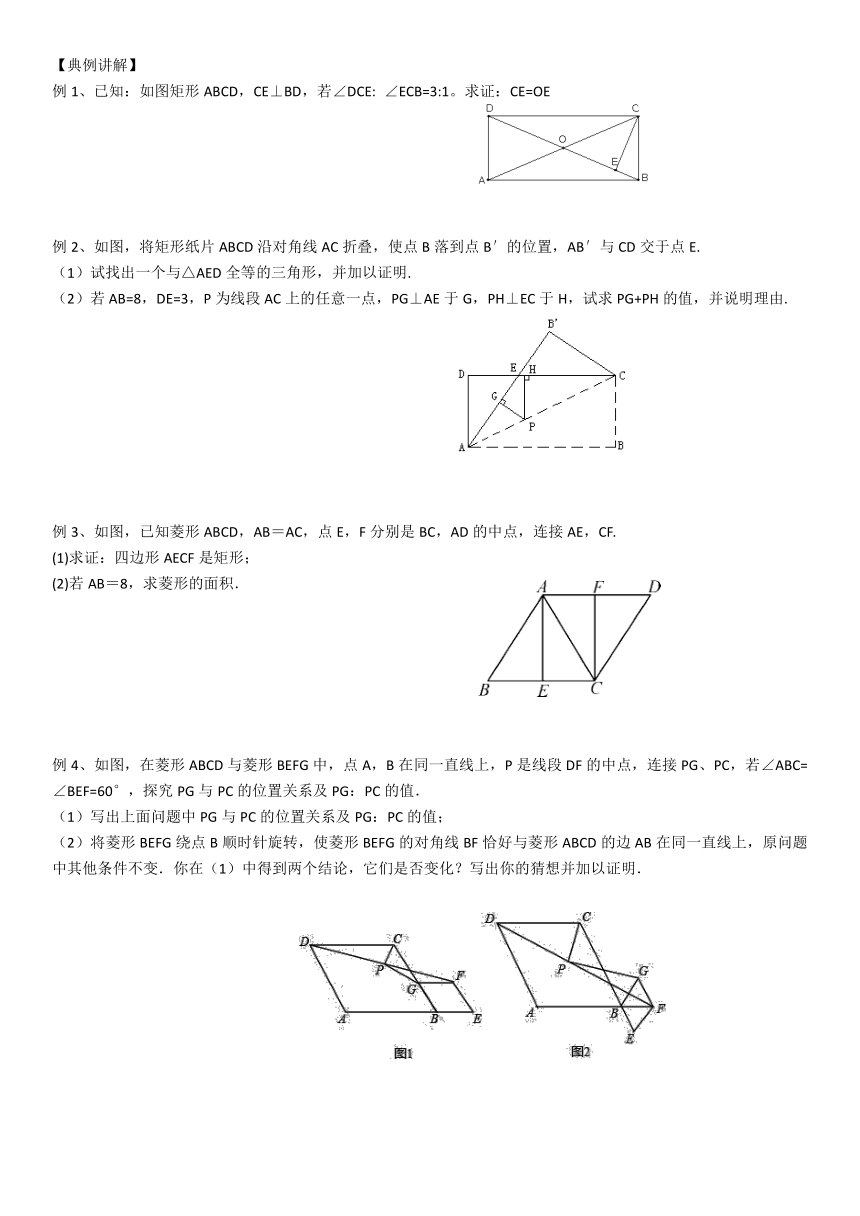
【知识要点复习】
1.四边形关系图:
2、特殊四边形的性质
边 角 对 角 线 对称性
平行四边形 对边 对角 两条对角线互相
矩 形 对边 四个角都是 两条对角线互相
菱 形 对边 四条边都 对角 两条对角线互相 , 每条对角线 一组对角
正方形 对边 四条边 四个角都是 两条对角线互相 , 每条对角线 一组对角
3.特殊四边形的常用判定方法
平行四边形 1、有两组 的四边形是平行四边形。 (定义) 2、两组 的四边形是平行四边形。 3、一组 的四边形是平行四边形。 4、 的四边形是平行四边形 (对角线) 5、 的四边形是平行四边形 (角)
矩 形 1、有一个角是 + 是矩 形 (定义) 2、有三个角是 的四边形是矩 形 3、对角线 的平行四边形是矩 形
菱 形 1、 + 是菱形 (定义) 2、 边都相等的四边形是菱形。 3、对角线 的平行四边形是菱形。
正方形 1、有一个角是 且有一组 的平行四边形是正方形(定义) 2、一组邻边相等 + 是正方形 3、一角为90°+ 是正方形
4. 其他重要定理
直角三角形的两条重要性质定理:(1)30°的直角三角形
(2)直角三角形斜边上的中线
5. 两条平行线间的距离的定义
若两条直线互相平行,则其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离,平行线间的距离__________.
6. 三角形的中位线
(1)三角形中位线的定义:连接三角线两边中点的线段叫做三角形的中位线
(2)三角形中位线定理:三角形的中位线__________________________________________.
7. 多边形的内角与外角和
(1)正多边形:在平面内,______________________________的多边形叫做正多边形
(2)多边形的内角和:n边形的内角和等于_________________________.
(3)多边形的外角和:多边形的外角和等于___________________.
(4)n边形的对角线有: _________________________.
【典例讲解】
例1、已知:如图矩形ABCD,CE⊥BD,若∠DCE: ∠ECB=3:1。求证:CE=OE
例2、如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
(1)试找出一个与△AED全等的三角形,并加以证明.
(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,试求PG+PH的值,并说明理由.
例3、如图,已知菱形ABCD,AB=AC,点E,F分别是BC,AD的中点,连接AE,CF.
(1)求证:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.
例4、如图,在菱形ABCD与菱形BEFG中,点A,B在同一直线上,P是线段DF的中点,连接PG、PC,若∠ABC=∠BEF=60°,探究PG与PC的位置关系及PG:PC的值.
(1)写出上面问题中PG与PC的位置关系及PG:PC的值;
(2)将菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一直线上,原问题中其他条件不变.你在(1)中得到两个结论,它们是否变化?写出你的猜想并加以证明.
课外作业: 姓名 _________ 班_________ 学号_________
一、选择题
1、下列说法正确的是 ( )
一组对边相等的四边形是平行四边形
一组对边平行,另一组对边相等的四边形是平行四边形
一组对角相等,一组对边平行的四边形是平行四边形
对角线互相垂直的四边形是平行四边形
2、如图,矩形ABCD的对角线AC=8 cm,∠AOD=120°,则AB的长为( )
A. cm B.2 cm C.2 cm D.4 cm
3、在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为( )
A. B. C. D. 8
4、 已知四边形的两条对角线相等,那么顺次连结四边形各边中点得到得四边形是( )
A.平行四边形 B.矩形 C. 菱形 D. 正方形
填空题
5、在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=14,BD=8,AB= ,那么的取值范围是 .
6、已知菱形的两条对角线长分别为12㎝和6㎝,那么这个菱形的面积为 ㎝2 .
7、矩形的两条对角线的一个夹角为60°两条对角线的和是8㎝,此矩形较短的边长是 ,较长边与对角线的夹角是 .
8、矩形一个角的平分线分矩形一边为1㎝和3㎝两部分,则这个矩形的面积为 .
9、如图,在△ABC中,点D,E,F分别在边BC,AB,CA上,且
DE∥CA,DF∥BA.下列四种说法:①四边形AEDF是平行四边形;②如
果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那
么四边形AEDF是菱形;④如果AD⊥BC且AB=AC,那么四边形AEDF
是菱形.其中,正确的有 .(填序号)
三、解答题
10、如图,△ABC中,AD是角平分线,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.
11、如图所示,将矩形ABCD沿着直线BD折叠,使点C落在C′,BC′交AD于E,AD=8,AB=4,
求△BED的面积.
12、如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:BD=EC;(2)若∠E=50°,求∠BAO的大小.
13、若四边形的四条边长a、b、c、d满足a4+b4+ c4+ d4=4abcd.求证:该四边形是菱形.
14、如图(1),在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转°得到四边形OAB'C',此时直线OA’、 直线B’C’分别与射线BC相交于点P、Q.
(1)四边形OABC的形状是 ,当=90°时,BP:BQ的值是 ;
(2)如图(2),当四边形OA’B’C’的顶点B’落在直线BC上时,求△OPB'的面积;
(3)在四边形OA’B’C’旋转过程中,当0°<а°≤180°时,是否存在这样的点P和点Q,使BP=0.5BQ?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(图1) (图2) (备用图)
四边形
F
E
D
C
B
A
C′
B
A
C
D
E
【知识要点复习】
1.四边形关系图:
2、特殊四边形的性质
边 角 对 角 线 对称性
平行四边形 对边 对角 两条对角线互相
矩 形 对边 四个角都是 两条对角线互相
菱 形 对边 四条边都 对角 两条对角线互相 , 每条对角线 一组对角
正方形 对边 四条边 四个角都是 两条对角线互相 , 每条对角线 一组对角
3.特殊四边形的常用判定方法
平行四边形 1、有两组 的四边形是平行四边形。 (定义) 2、两组 的四边形是平行四边形。 3、一组 的四边形是平行四边形。 4、 的四边形是平行四边形 (对角线) 5、 的四边形是平行四边形 (角)
矩 形 1、有一个角是 + 是矩 形 (定义) 2、有三个角是 的四边形是矩 形 3、对角线 的平行四边形是矩 形
菱 形 1、 + 是菱形 (定义) 2、 边都相等的四边形是菱形。 3、对角线 的平行四边形是菱形。
正方形 1、有一个角是 且有一组 的平行四边形是正方形(定义) 2、一组邻边相等 + 是正方形 3、一角为90°+ 是正方形
4. 其他重要定理
直角三角形的两条重要性质定理:(1)30°的直角三角形
(2)直角三角形斜边上的中线
5. 两条平行线间的距离的定义
若两条直线互相平行,则其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离,平行线间的距离__________.
6. 三角形的中位线
(1)三角形中位线的定义:连接三角线两边中点的线段叫做三角形的中位线
(2)三角形中位线定理:三角形的中位线__________________________________________.
7. 多边形的内角与外角和
(1)正多边形:在平面内,______________________________的多边形叫做正多边形
(2)多边形的内角和:n边形的内角和等于_________________________.
(3)多边形的外角和:多边形的外角和等于___________________.
(4)n边形的对角线有: _________________________.
【典例讲解】
例1、已知:如图矩形ABCD,CE⊥BD,若∠DCE: ∠ECB=3:1。求证:CE=OE
例2、如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
(1)试找出一个与△AED全等的三角形,并加以证明.
(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,试求PG+PH的值,并说明理由.
例3、如图,已知菱形ABCD,AB=AC,点E,F分别是BC,AD的中点,连接AE,CF.
(1)求证:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.
例4、如图,在菱形ABCD与菱形BEFG中,点A,B在同一直线上,P是线段DF的中点,连接PG、PC,若∠ABC=∠BEF=60°,探究PG与PC的位置关系及PG:PC的值.
(1)写出上面问题中PG与PC的位置关系及PG:PC的值;
(2)将菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一直线上,原问题中其他条件不变.你在(1)中得到两个结论,它们是否变化?写出你的猜想并加以证明.
课外作业: 姓名 _________ 班_________ 学号_________
一、选择题
1、下列说法正确的是 ( )
一组对边相等的四边形是平行四边形
一组对边平行,另一组对边相等的四边形是平行四边形
一组对角相等,一组对边平行的四边形是平行四边形
对角线互相垂直的四边形是平行四边形
2、如图,矩形ABCD的对角线AC=8 cm,∠AOD=120°,则AB的长为( )
A. cm B.2 cm C.2 cm D.4 cm
3、在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为( )
A. B. C. D. 8
4、 已知四边形的两条对角线相等,那么顺次连结四边形各边中点得到得四边形是( )
A.平行四边形 B.矩形 C. 菱形 D. 正方形
填空题
5、在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=14,BD=8,AB= ,那么的取值范围是 .
6、已知菱形的两条对角线长分别为12㎝和6㎝,那么这个菱形的面积为 ㎝2 .
7、矩形的两条对角线的一个夹角为60°两条对角线的和是8㎝,此矩形较短的边长是 ,较长边与对角线的夹角是 .
8、矩形一个角的平分线分矩形一边为1㎝和3㎝两部分,则这个矩形的面积为 .
9、如图,在△ABC中,点D,E,F分别在边BC,AB,CA上,且
DE∥CA,DF∥BA.下列四种说法:①四边形AEDF是平行四边形;②如
果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那
么四边形AEDF是菱形;④如果AD⊥BC且AB=AC,那么四边形AEDF
是菱形.其中,正确的有 .(填序号)
三、解答题
10、如图,△ABC中,AD是角平分线,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.
11、如图所示,将矩形ABCD沿着直线BD折叠,使点C落在C′,BC′交AD于E,AD=8,AB=4,
求△BED的面积.
12、如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:BD=EC;(2)若∠E=50°,求∠BAO的大小.
13、若四边形的四条边长a、b、c、d满足a4+b4+ c4+ d4=4abcd.求证:该四边形是菱形.
14、如图(1),在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转°得到四边形OAB'C',此时直线OA’、 直线B’C’分别与射线BC相交于点P、Q.
(1)四边形OABC的形状是 ,当=90°时,BP:BQ的值是 ;
(2)如图(2),当四边形OA’B’C’的顶点B’落在直线BC上时,求△OPB'的面积;
(3)在四边形OA’B’C’旋转过程中,当0°<а°≤180°时,是否存在这样的点P和点Q,使BP=0.5BQ?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(图1) (图2) (备用图)
四边形
F
E
D
C
B
A
C′
B
A
C
D
E
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
