人教版六年级下册数学课件 圆柱的体积——水面升高多少厘米(动画演示)(共17张PPT)
文档属性
| 名称 | 人教版六年级下册数学课件 圆柱的体积——水面升高多少厘米(动画演示)(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
六年:圆柱的体积
——水面升高多少厘米
水面升降问题
一学就会
金色绿叶
(动画演示)
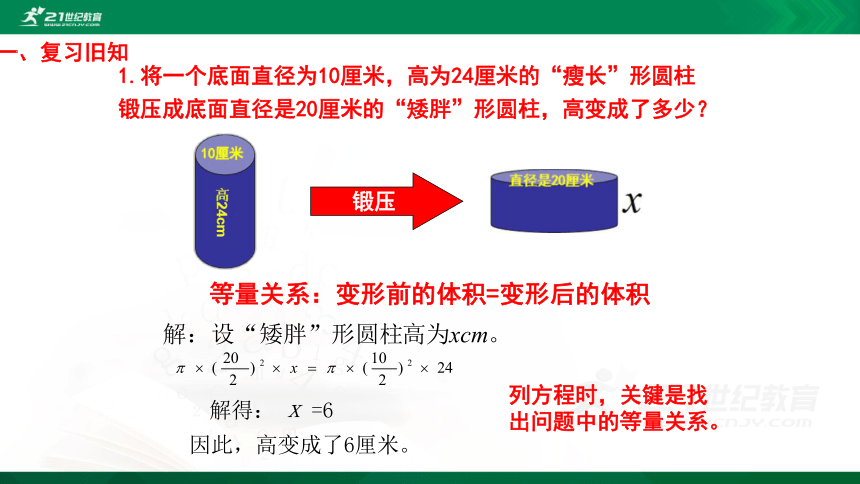
1.将一个底面直径为10厘米,高为24厘米的“瘦长”形圆柱锻压成底面直径是20厘米的“矮胖”形圆柱,高变成了多少?
一、复习旧知
锻压
等量关系:变形前的体积=变形后的体积
解得: x =6
因此,高变成了6厘米。
列方程时,关键是找出问题中的等量关系。
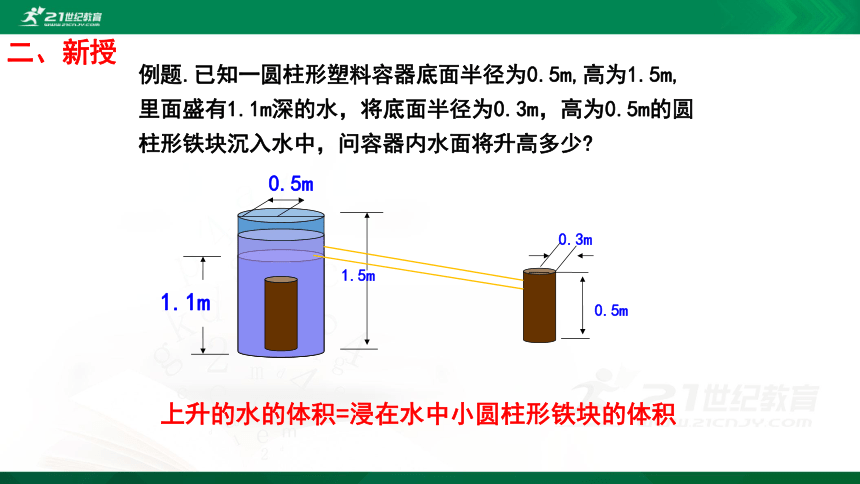
例题.已知一圆柱形塑料容器底面半径为0.5m,高为1.5m,里面盛有1.1m深的水,将底面半径为0.3m,高为0.5m的圆柱形铁块沉入水中,问容器内水面将升高多少
1.5m
0.5m
0.5m
0.3m
二、新授
1.1m
上升的水的体积=浸在水中小圆柱形铁块的体积
1.5m
0.5m
0.3m
1.1m
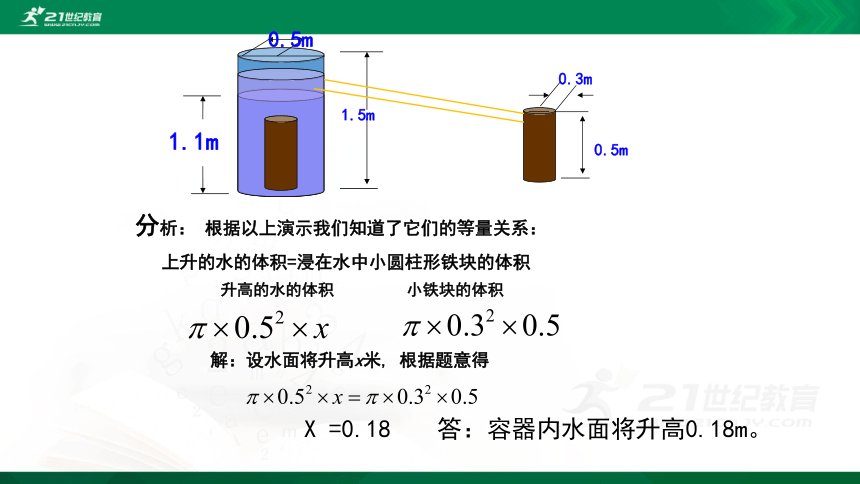
分析: 根据以上演示我们知道了它们的等量关系:
上升的水的体积=浸在水中小圆柱形铁块的体积
小铁块的体积
解:设水面将升高x米, 根据题意得
X =0.18
答:容器内水面将升高0.18m。
升高的水的体积
0.5m
1、把一块长31.4cm、宽2cm、高4cm的长方体钢坯熔铸成底面半径是4cm的圆柱,圆柱的高是多少厘米?
把长方体熔铸成圆柱,形状变了体积没有发生变化,长方体的体积等于圆柱的体积,再通过圆柱体积÷圆柱底面积=高的公式可求出圆柱的高。
31.4×2×4÷(3.14×42)
=251.2÷50.24
=5(cm)
答:圆柱的高是5cm。
三、巩固应用
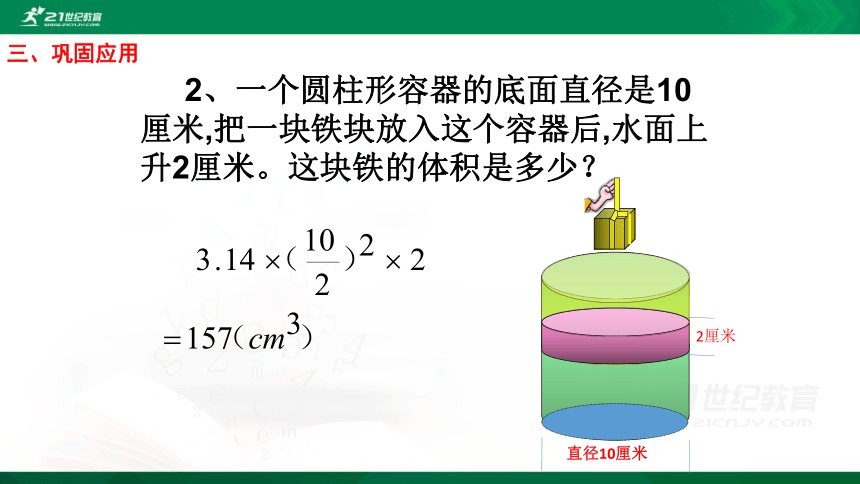
2、一个圆柱形容器的底面直径是10厘米,把一块铁块放入这个容器后,水面上升2厘米。这块铁的体积是多少?
直径10厘米
2厘米
三、巩固应用
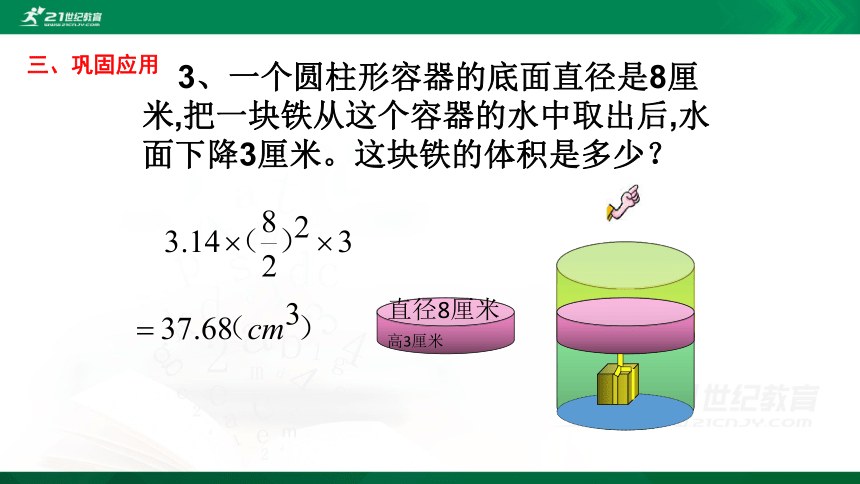
3、一个圆柱形容器的底面直径是8厘米,把一块铁从这个容器的水中取出后,水面下降3厘米。这块铁的体积是多少?
三、巩固应用
直径8厘米
高3厘米
4、一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸在这个容器的水中的铁块取出后,水面下降2cm。这块铁块的体积是多少?
综合练习
想:铁块的体积就是高度为2cm的圆柱体积。
3.14×(10÷2)2×2
=3.14×25×2
=157(cm3)
答:这块铁块的体积157cm3。
容器的底面积×变化的水面高度=物体的体积
排水法
5、一只底面半径是20厘米的贮水桶,把一段直径是10厘米的圆钢浸入水中,这时水面升高了2厘米,求这段圆钢的长是多少厘米?
容器的底面积×变化的水面高度=浸在水中物体的体积
想:先利用排水法求圆柱的体积。
1
1
16
1
=32(cm)
答:这段圆钢的长是32cm。
半径是20厘米
直径是10厘米
水升高2厘米
6、一个装有水的圆柱形容器,底面直径是10厘米;现将一个底面直径是4厘米,高15厘米的圆柱形零件完全浸没水中,水面上升了多少厘米?
容器的底面积×变化的水面高度=物体的体积
物体的体积÷容器的底面积=变化的水面高度
1
1
3
5
=2.4(cm)
答:水面上升了2.4cm。
一圆柱体容器的内半径为3厘米,内壁高30厘米,容器内盛有15厘米高的水。现将一个底面半径为2厘米、高18厘米的金属圆柱竖直放入容器内,问容器的水将升高多少米?
四、拔高题
一圆柱体容器的内半径为3厘米,内壁高30厘米,容器内盛有15厘米高的水。现将一个底面半径为2厘米、高18厘米的金属圆柱竖直放入容器内,问容器的水将升高多少米?
分析:本题涉及圆柱的体积v= π r2h,这里r是圆柱底面半径,h为圆柱的高。一个金属圆柱竖直放入容器内,会出现两种可能:
(1)容器内的水升高后不淹没放入的金属圆柱;(2) 容器内的水升高后 淹没放入的金属圆柱 。
因此列方程求解时要分两种情况。
四、拔高题
3cm
15cm
30cm
半径:2cm
18cm
分析:难点在浸在水中的圆柱体高度是多少不知道,所以浸在水中圆柱体体积不知怎样求。
质疑:小圆柱体垂直放入水中不会让水溢出,我们可结合生活经验理解。
答案与完全浸在水中答案矛盾,显然此答案不可能。
所以,容器内的水升高8厘米。
教师质疑:如果插入的圆柱体高10米,其它条件不变,显然是不能完全浸入水中的,那么水面会升高多少厘米,你敢尝试么?
利用了体积不变的特性,把不规则图形转化成规则图形来计算。
六年:圆柱的体积
——水面升高多少厘米
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
六年:圆柱的体积
——水面升高多少厘米
水面升降问题
一学就会
金色绿叶
(动画演示)
1.将一个底面直径为10厘米,高为24厘米的“瘦长”形圆柱锻压成底面直径是20厘米的“矮胖”形圆柱,高变成了多少?
一、复习旧知
锻压
等量关系:变形前的体积=变形后的体积
解得: x =6
因此,高变成了6厘米。
列方程时,关键是找出问题中的等量关系。
例题.已知一圆柱形塑料容器底面半径为0.5m,高为1.5m,里面盛有1.1m深的水,将底面半径为0.3m,高为0.5m的圆柱形铁块沉入水中,问容器内水面将升高多少
1.5m
0.5m
0.5m
0.3m
二、新授
1.1m
上升的水的体积=浸在水中小圆柱形铁块的体积
1.5m
0.5m
0.3m
1.1m
分析: 根据以上演示我们知道了它们的等量关系:
上升的水的体积=浸在水中小圆柱形铁块的体积
小铁块的体积
解:设水面将升高x米, 根据题意得
X =0.18
答:容器内水面将升高0.18m。
升高的水的体积
0.5m
1、把一块长31.4cm、宽2cm、高4cm的长方体钢坯熔铸成底面半径是4cm的圆柱,圆柱的高是多少厘米?
把长方体熔铸成圆柱,形状变了体积没有发生变化,长方体的体积等于圆柱的体积,再通过圆柱体积÷圆柱底面积=高的公式可求出圆柱的高。
31.4×2×4÷(3.14×42)
=251.2÷50.24
=5(cm)
答:圆柱的高是5cm。
三、巩固应用
2、一个圆柱形容器的底面直径是10厘米,把一块铁块放入这个容器后,水面上升2厘米。这块铁的体积是多少?
直径10厘米
2厘米
三、巩固应用
3、一个圆柱形容器的底面直径是8厘米,把一块铁从这个容器的水中取出后,水面下降3厘米。这块铁的体积是多少?
三、巩固应用
直径8厘米
高3厘米
4、一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸在这个容器的水中的铁块取出后,水面下降2cm。这块铁块的体积是多少?
综合练习
想:铁块的体积就是高度为2cm的圆柱体积。
3.14×(10÷2)2×2
=3.14×25×2
=157(cm3)
答:这块铁块的体积157cm3。
容器的底面积×变化的水面高度=物体的体积
排水法
5、一只底面半径是20厘米的贮水桶,把一段直径是10厘米的圆钢浸入水中,这时水面升高了2厘米,求这段圆钢的长是多少厘米?
容器的底面积×变化的水面高度=浸在水中物体的体积
想:先利用排水法求圆柱的体积。
1
1
16
1
=32(cm)
答:这段圆钢的长是32cm。
半径是20厘米
直径是10厘米
水升高2厘米
6、一个装有水的圆柱形容器,底面直径是10厘米;现将一个底面直径是4厘米,高15厘米的圆柱形零件完全浸没水中,水面上升了多少厘米?
容器的底面积×变化的水面高度=物体的体积
物体的体积÷容器的底面积=变化的水面高度
1
1
3
5
=2.4(cm)
答:水面上升了2.4cm。
一圆柱体容器的内半径为3厘米,内壁高30厘米,容器内盛有15厘米高的水。现将一个底面半径为2厘米、高18厘米的金属圆柱竖直放入容器内,问容器的水将升高多少米?
四、拔高题
一圆柱体容器的内半径为3厘米,内壁高30厘米,容器内盛有15厘米高的水。现将一个底面半径为2厘米、高18厘米的金属圆柱竖直放入容器内,问容器的水将升高多少米?
分析:本题涉及圆柱的体积v= π r2h,这里r是圆柱底面半径,h为圆柱的高。一个金属圆柱竖直放入容器内,会出现两种可能:
(1)容器内的水升高后不淹没放入的金属圆柱;(2) 容器内的水升高后 淹没放入的金属圆柱 。
因此列方程求解时要分两种情况。
四、拔高题
3cm
15cm
30cm
半径:2cm
18cm
分析:难点在浸在水中的圆柱体高度是多少不知道,所以浸在水中圆柱体体积不知怎样求。
质疑:小圆柱体垂直放入水中不会让水溢出,我们可结合生活经验理解。
答案与完全浸在水中答案矛盾,显然此答案不可能。
所以,容器内的水升高8厘米。
教师质疑:如果插入的圆柱体高10米,其它条件不变,显然是不能完全浸入水中的,那么水面会升高多少厘米,你敢尝试么?
利用了体积不变的特性,把不规则图形转化成规则图形来计算。
六年:圆柱的体积
——水面升高多少厘米
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
