人教版高一物理必修二第五章 5.1曲线运动之小船过河(22张ppt) 课件
文档属性
| 名称 | 人教版高一物理必修二第五章 5.1曲线运动之小船过河(22张ppt) 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 903.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-16 20:04:26 | ||
图片预览







文档简介
(共22张PPT)
1.2 运动的合成与分解
第一章 抛体运动
小船过河
绳杆末端速度分解问题
例1:一艘小船在100m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是4m/s,求:(1)欲使船渡河时间最短,船应该怎样渡河?最短时间是多少?船经过的位移多大?
典型问题1、小船过河
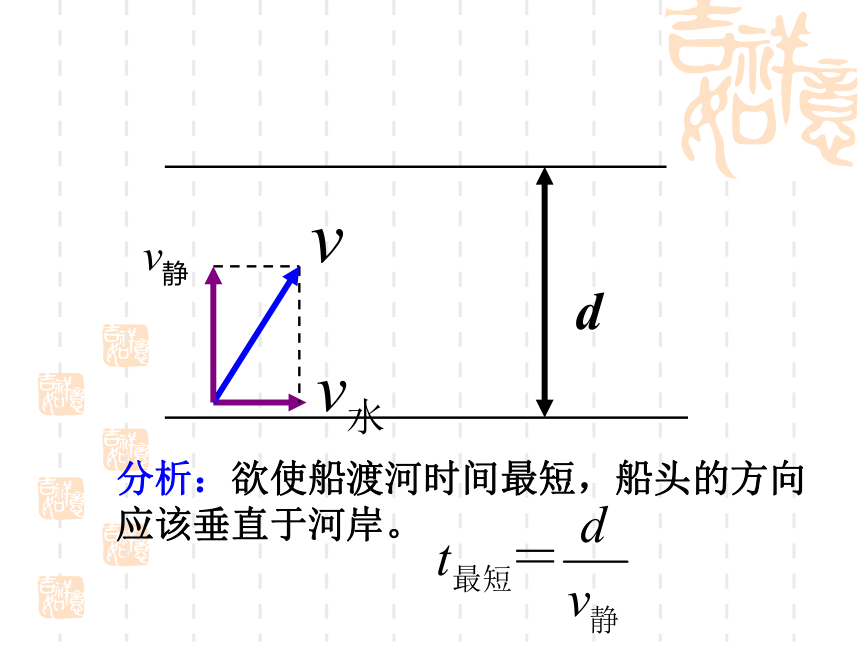
d
分析:欲使船渡河时间最短,船头的方向应该垂直于河岸。
最短时间
此时合速度
此时航程
解:当船头垂直河岸时,所用时间最短
例1:一艘小船在100m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是4m/s,求:(2)欲使航行距离最短,船应该怎样渡河?渡河时间多长?
15.一艘小船在 200m宽的河中横渡到对岸,已知水流速度是2m/s,小船在静水中的速度是4m/s,求:
①当船头始终正对着对岸时,小船多长时间到达对岸,小船实际运行了多远?
②如果小船的路径要与河岸垂直,应如何行驶?消耗的时间是多少?
③如果小船要用最短时间过河,应如何?船行最短时间为多少?
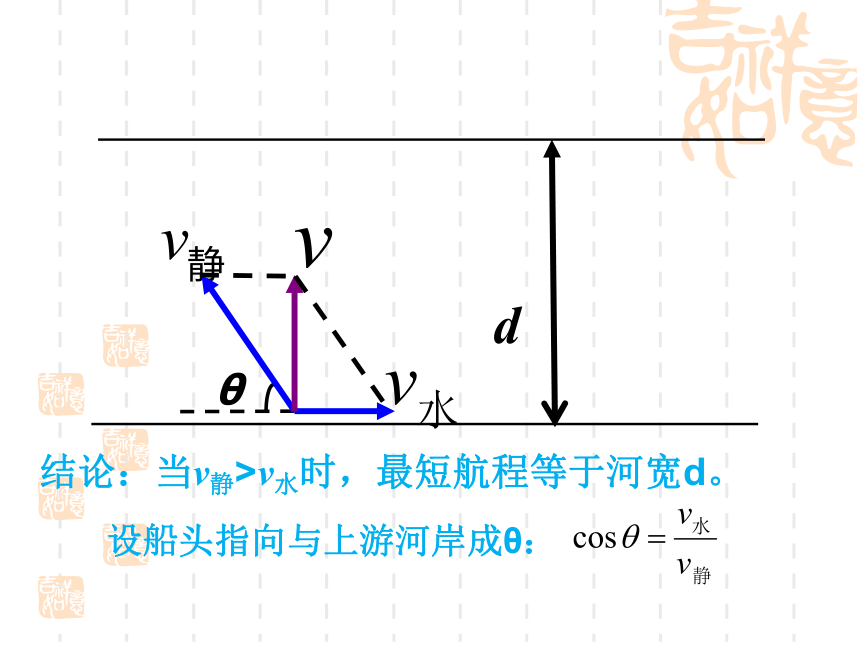
θ
d
设船头指向与上游河岸成θ:
结论:当v静>v水时,最短航程等于河宽d。
过河时间:
合速度:
则
解:1.当船头指向斜上游,与岸夹角为?时,合运动垂直河岸,航程最短,数值等于河宽100m.
练习1.船在400米宽的河中横渡,河水流速是2m/s,船在静水中的航速是4m/s,试求:
(1)要使船到达对岸的时间最短,船头应指向何处?最短时间是多少?
(2)要使船航程最短,船头应指向何处?最短航程为多少?
例2:若河宽仍为100m,已知水流速度是4m/s,小船在静水中的速度是3m/s.(注意:v静求:
(1)欲使船渡河时间最短,船应该怎样渡河?
(2)欲使航行距离最短,船应该怎样渡河?最短航线是河宽吗?
在v静和v水合成的所有合速度中,以v水矢量末端为圆心,以v静矢量的大小为半径画弧,从v水矢量的始端向圆弧作切线,则合速度沿此切线方向航程最短.
θ
θ
结论:当v静< v水时,最短航程不等于河宽d。
船头指向与上游河岸成θ:
1.小船过河问题分析
(1)船的实际运动是水流的运动和船相对静水的
运动的合运动.
(2)三种速度:v静(船在静水中的速度)、v水(水的
流速)、v船(船的实际速度).
(3)三种情景
①过河时间最短:船头正对河岸时,渡河时间最
短, (d为河宽).
②过河路径最短(v静>v水时):合速度垂直于河岸,
航程最短,s短=d
典型问题:
③过河路径最短(v静岸,无法垂直渡河.确定方法如下:如图所示,以v水矢量末端为圆心,以v静矢量的大小为半径画弧,从v水矢量的始端向圆弧作切线,则合速度沿此切线方向航程最短.
图2
v水
v静
v静
如果:
1、在船头始终垂直对岸的情况下,在行驶到河中间时,水流速度突然增大,过河时间如何变化?
2、为了垂直到达河对岸,在行驶到河中间时,水流速度突然增大,过河时间如何变化?
答案:变长
答案:不变
解析:水的速度增加,且为了垂直到达河对岸,所以船在沿水的方向的分速度增加,垂直分量减小。使时间增加。
典型问题2、绳杆末端速度分解问题
绳子末端运动的效果有两个:一个是沿牵引方向的平动效果,改变速度的大小;二是垂直于牵引方向的转动效果,改变速度的方向.因此,此类问题中两分运动的方向分别为沿绳和垂直于绳的方向.
2.绳连物体的速度分解问题
原则:把物体的实际速度分解为垂直于绳和沿绳方向的两个分速度,根据绳连物体沿绳方向的分速度大小相等求解。
【同一根绳子上,张力大小处处相等,运动情况相同】
例:如图5所示,物体A和B质量均为m,且分别与轻绳连接跨过光滑轻质定滑轮,B放在水平面上,A与悬绳竖直.用力F拉B沿水平面向左“匀速”运动过程中,绳对A的拉力的大小是( )
A.大于mg
B.总等于mg
C.一定小于mg
D.以上三项都不正确
绳拉物体或物体拉绳问题的主要思路:
(1)物体的实际运动为合运动;
(2)沿绳的运动为一个分运动;
(3)垂直于绳的运动为另一个分运动。
解析 物体B向左的速度vB是合速度,
根据其效果,分解为如右图所示的两
个速度v1和v2,其中v2=vA,又因v2=
vBcosθ,当物体B向左匀速运动时,
vB大小不变,θ变小,cosθ增大,所以
v2增大,即物体A向上做加速运动,由牛顿第二定律得:FT-mg=ma,可知:FT=mg+ma>mg,故A正确.
答案 A
方法提炼
在进行速度分解时,首先要分清合速度与分速度.
合速度就是物体实际运动的速度,由物体的实际运
动确定,分速度由合速度的效果利用平行四边形定
则确定.
练习 1、如图6所示,汽车向右沿水平面做匀速直线运动,通过绳子提升重物M.若不计绳子质量和绳子与滑轮间的摩擦,则在提升重物的过程中,下列有关判断正确的是( )
A.重物加速上升
B.重物减速上升
C.绳子张力不断减小
D.地面对汽车的支持力增大
图6
ACD
分析:将小车的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向的速度等于M的速度,根据A的运动情况得出M的加速度方向,得知物体运动情况
解析:A、设绳子与水平方向的夹角为α,将小车的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向的速度等于M的速度,
根据平行四边形定则得,vM=vcosα,车子在匀速向右的运动过程中,绳子与水平方向的夹角为α减小,
所以M的速度增大,M做加速上升运动,且拉力大于重物的重力,故A正确,B错误;
C、车速一定 重物速度随着角度的减小,速度逐渐加快,重物在做加速上升,角度越来越小,由vM=vcosα,可知,在相等的时间内,速度的增加变小,则加速度也越来越小【由“余弦函数图像”递推到“速度-时间图像”可得】,绳子张力等于Mg+Ma,故C正确;
D、对小车受力分析可知,地面对小车的支持力增大.
答案:ACD
点评:解决本题的关键会对小车的速度进行分解,知道小车的速度是沿绳子方向和垂直于绳子方向速度的合速度.
1.2 运动的合成与分解
第一章 抛体运动
小船过河
绳杆末端速度分解问题
例1:一艘小船在100m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是4m/s,求:(1)欲使船渡河时间最短,船应该怎样渡河?最短时间是多少?船经过的位移多大?
典型问题1、小船过河
d
分析:欲使船渡河时间最短,船头的方向应该垂直于河岸。
最短时间
此时合速度
此时航程
解:当船头垂直河岸时,所用时间最短
例1:一艘小船在100m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是4m/s,求:(2)欲使航行距离最短,船应该怎样渡河?渡河时间多长?
15.一艘小船在 200m宽的河中横渡到对岸,已知水流速度是2m/s,小船在静水中的速度是4m/s,求:
①当船头始终正对着对岸时,小船多长时间到达对岸,小船实际运行了多远?
②如果小船的路径要与河岸垂直,应如何行驶?消耗的时间是多少?
③如果小船要用最短时间过河,应如何?船行最短时间为多少?
θ
d
设船头指向与上游河岸成θ:
结论:当v静>v水时,最短航程等于河宽d。
过河时间:
合速度:
则
解:1.当船头指向斜上游,与岸夹角为?时,合运动垂直河岸,航程最短,数值等于河宽100m.
练习1.船在400米宽的河中横渡,河水流速是2m/s,船在静水中的航速是4m/s,试求:
(1)要使船到达对岸的时间最短,船头应指向何处?最短时间是多少?
(2)要使船航程最短,船头应指向何处?最短航程为多少?
例2:若河宽仍为100m,已知水流速度是4m/s,小船在静水中的速度是3m/s.(注意:v静
(1)欲使船渡河时间最短,船应该怎样渡河?
(2)欲使航行距离最短,船应该怎样渡河?最短航线是河宽吗?
在v静和v水合成的所有合速度中,以v水矢量末端为圆心,以v静矢量的大小为半径画弧,从v水矢量的始端向圆弧作切线,则合速度沿此切线方向航程最短.
θ
θ
结论:当v静< v水时,最短航程不等于河宽d。
船头指向与上游河岸成θ:
1.小船过河问题分析
(1)船的实际运动是水流的运动和船相对静水的
运动的合运动.
(2)三种速度:v静(船在静水中的速度)、v水(水的
流速)、v船(船的实际速度).
(3)三种情景
①过河时间最短:船头正对河岸时,渡河时间最
短, (d为河宽).
②过河路径最短(v静>v水时):合速度垂直于河岸,
航程最短,s短=d
典型问题:
③过河路径最短(v静
图2
v水
v静
v静
如果:
1、在船头始终垂直对岸的情况下,在行驶到河中间时,水流速度突然增大,过河时间如何变化?
2、为了垂直到达河对岸,在行驶到河中间时,水流速度突然增大,过河时间如何变化?
答案:变长
答案:不变
解析:水的速度增加,且为了垂直到达河对岸,所以船在沿水的方向的分速度增加,垂直分量减小。使时间增加。
典型问题2、绳杆末端速度分解问题
绳子末端运动的效果有两个:一个是沿牵引方向的平动效果,改变速度的大小;二是垂直于牵引方向的转动效果,改变速度的方向.因此,此类问题中两分运动的方向分别为沿绳和垂直于绳的方向.
2.绳连物体的速度分解问题
原则:把物体的实际速度分解为垂直于绳和沿绳方向的两个分速度,根据绳连物体沿绳方向的分速度大小相等求解。
【同一根绳子上,张力大小处处相等,运动情况相同】
例:如图5所示,物体A和B质量均为m,且分别与轻绳连接跨过光滑轻质定滑轮,B放在水平面上,A与悬绳竖直.用力F拉B沿水平面向左“匀速”运动过程中,绳对A的拉力的大小是( )
A.大于mg
B.总等于mg
C.一定小于mg
D.以上三项都不正确
绳拉物体或物体拉绳问题的主要思路:
(1)物体的实际运动为合运动;
(2)沿绳的运动为一个分运动;
(3)垂直于绳的运动为另一个分运动。
解析 物体B向左的速度vB是合速度,
根据其效果,分解为如右图所示的两
个速度v1和v2,其中v2=vA,又因v2=
vBcosθ,当物体B向左匀速运动时,
vB大小不变,θ变小,cosθ增大,所以
v2增大,即物体A向上做加速运动,由牛顿第二定律得:FT-mg=ma,可知:FT=mg+ma>mg,故A正确.
答案 A
方法提炼
在进行速度分解时,首先要分清合速度与分速度.
合速度就是物体实际运动的速度,由物体的实际运
动确定,分速度由合速度的效果利用平行四边形定
则确定.
练习 1、如图6所示,汽车向右沿水平面做匀速直线运动,通过绳子提升重物M.若不计绳子质量和绳子与滑轮间的摩擦,则在提升重物的过程中,下列有关判断正确的是( )
A.重物加速上升
B.重物减速上升
C.绳子张力不断减小
D.地面对汽车的支持力增大
图6
ACD
分析:将小车的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向的速度等于M的速度,根据A的运动情况得出M的加速度方向,得知物体运动情况
解析:A、设绳子与水平方向的夹角为α,将小车的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向的速度等于M的速度,
根据平行四边形定则得,vM=vcosα,车子在匀速向右的运动过程中,绳子与水平方向的夹角为α减小,
所以M的速度增大,M做加速上升运动,且拉力大于重物的重力,故A正确,B错误;
C、车速一定 重物速度随着角度的减小,速度逐渐加快,重物在做加速上升,角度越来越小,由vM=vcosα,可知,在相等的时间内,速度的增加变小,则加速度也越来越小【由“余弦函数图像”递推到“速度-时间图像”可得】,绳子张力等于Mg+Ma,故C正确;
D、对小车受力分析可知,地面对小车的支持力增大.
答案:ACD
点评:解决本题的关键会对小车的速度进行分解,知道小车的速度是沿绳子方向和垂直于绳子方向速度的合速度.
