1.1.2 弧度制课件 (共30张PPT)
文档属性
| 名称 | 1.1.2 弧度制课件 (共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-18 18:35:57 | ||
图片预览









文档简介
课件30张PPT。1.1.2 弧度制CONTENTS PART 01学习目标
PART 02问题导学
PART 03题型探究
PART 04达标检测
1234学习目标1.理解角度制与弧度制的概念,能对弧度和角度进行正确的转换.
2.体会引入弧度制的必要性,建立角的集合与实数集一一对应关系
3.掌握并能应用弧度制下的弧长公式和扇形面积公式.问题导学1.度量角的单位制
(1)角度制
用 作为单位来度量角的单位制叫做角度制,规定1度的角等于周角的 .
(2)弧度制
①弧度制的定义
长度等于 的弧所对的圆心角叫做1弧度的角,用符号rad表示,读作弧度.以 作为单位来度量角的单位制叫做弧度制.度半径长弧度②任意角的弧度数与实数的对应关系
正角的弧度数是一个 ;负角的弧度数是一个 ;零角的弧度数是 .
③角的弧度数的计算
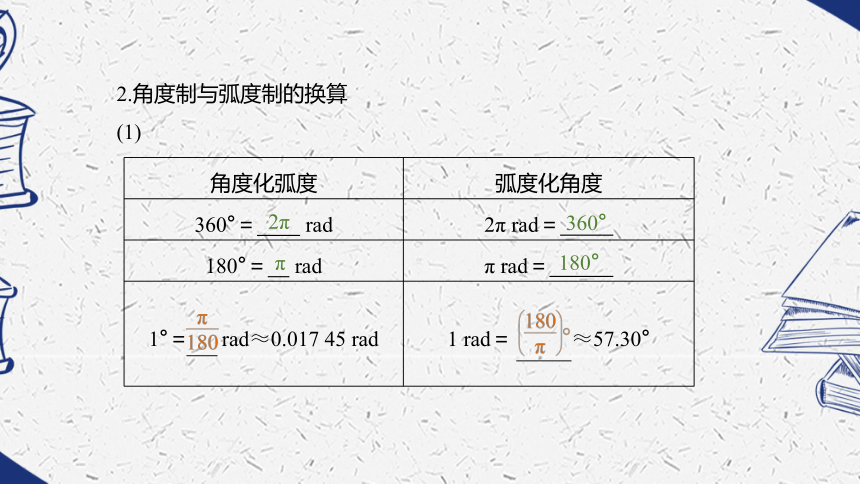
如果半径为r的圆的圆心角α所对弧的长为l,那么,角α的弧度数的绝对值是|α|= .正数负数零2.角度制与弧度制的换算
(1)2π360°π180°(2)一些特殊角的度数与弧度数的对应关系3.扇形的弧长及面积公式
设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则??题型探究思考1 1弧度的角是怎样规定的?1弧度的角和圆半径的大小有关吗?你能作出一个1弧度的角吗?
答 把长度等于半径长的弧所对的圆心角叫做1
弧度的角.1弧度的角是一个定值,与所在圆的半
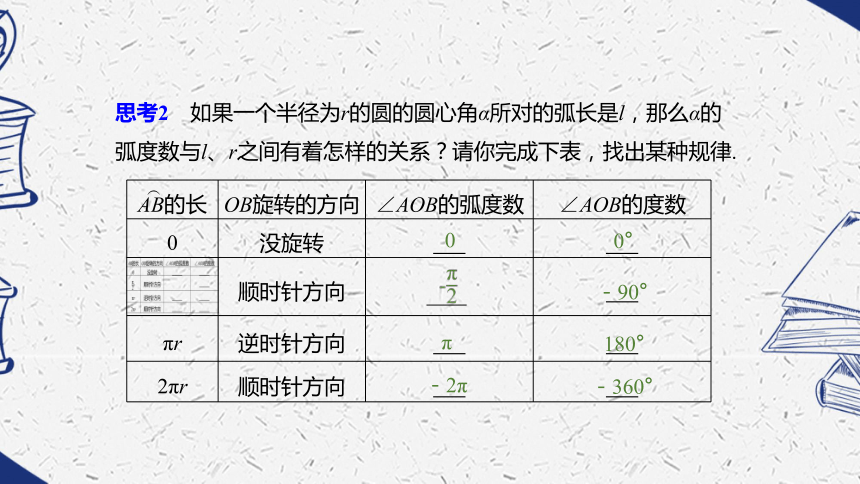
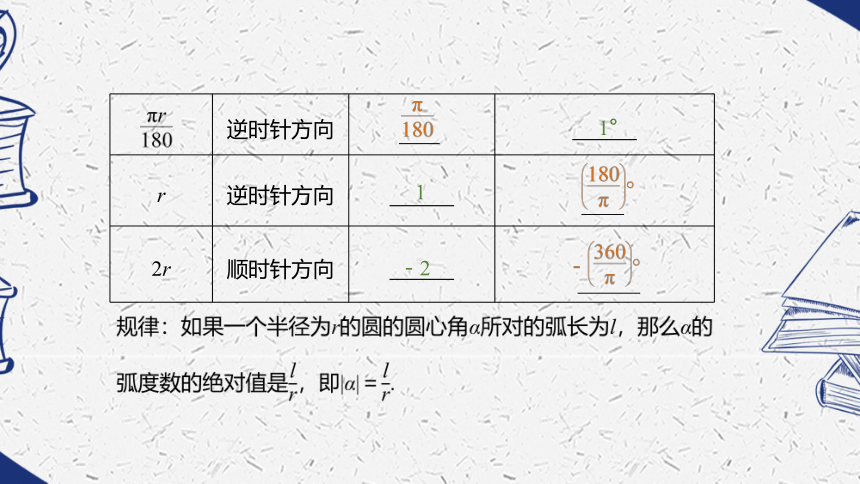
径无关.如图所示,∠AOB就是1弧度的角.思考2 如果一个半径为r的圆的圆心角α所对的弧长是l,那么α的弧度数与l、r之间有着怎样的关系?请你完成下表,找出某种规律. 00°-90°π180°-2π-360°(?1°1-2反思及感悟小结 一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.如果半径为r的圆的圆心角α所对弧的长为l,那么,角α的弧度数的绝对值是|α|="l" /"r" .这里,α的正负由角α的终边的旋转方向决定.思考3 角度制与弧度制换算时,灵活运用下表中的对应关系,请补充完整.2π360°π180°例1 (1)把67°30′化成弧度;反思及感悟将角度转化为弧度时,要把带有分、秒的部分化为度之后,牢记π rad=180°即可求解.把弧度转化为角度时,直接用弧度数乘以 即可.??288探究点二 弧度制下的弧长公式和扇形面积公式思考 我们已经学习过角度制下的弧长公式和扇形面积公式,请根据“一周角(即360°)的弧度数为2π”这一事实化简上述公式.(设半径为r,圆心角弧度数为α).例2 已知一扇形的周长为40 cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
解 设扇形的圆心角为θ,半径为r,弧长为l,面积为S,
则l+2r=40,∴l=40-2r.∴当半径r=10 cm时,扇形的面积最大,最大值为100 cm2,所以当扇形的圆心角为2 rad,半径为10 cm时,扇形的面积最大为100 cm2.反思及感悟灵活运用扇形弧长公式、面积公式列方程组求解是解决此类问题的关键,有时运用函数思想、转化思想解决扇形中的有关最值问题,将扇形面积表示为半径的函数,转化为r的二次函数的最值问题.?探究点三 利用弧度制表示终边相同的角导引 在弧度制下,与α终边相同的角连同α在内可以表示为2kπ+α(k∈Z),其中α的单位必须是弧度.
思考1 利用弧度制表示出终边落在坐标轴上的角的集合.思考2 利用弧度制表示出终边落在各个象限的角的集合.?解 (1)∵-1 500°=-1 800°+300°=-5×360°+300°.∴-4与2π-4终边相同,是第二象限角.跟踪训练3 (1)把-1 480°写成α+2kπ(k∈Z)的形式,其中0≤α<2π;(2)若β∈[-4π,0],且β与(1)中α的终边相同,求β.又β∈[-4 π ,0],达标检测1.时针经过一小时,时针转过了( )解析 时针经过一小时,转过-30°,B2.已知扇形的周长是6 cm,面积是2 cm2,则扇形的中心角的弧度数是( )
A.1 B.1或2 C.1或4 D.2或4
解析 设扇形半径为r,中心角弧度数为α,C3.已知两角的和是1弧度,两角的差是1°,则这两个角分别为__________________.
解析 设这两个角为α,β弧度,不妨设α>β,规律及方法1.角的概念推广后,在弧度制下,角的集合与实数集R之间建立起一一对应的关系:每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.3.在弧度制下,扇形的弧长公式及面积公式都得到了简化,具体应用时,要注意角的单位取弧度.
PART 02问题导学
PART 03题型探究
PART 04达标检测
1234学习目标1.理解角度制与弧度制的概念,能对弧度和角度进行正确的转换.
2.体会引入弧度制的必要性,建立角的集合与实数集一一对应关系
3.掌握并能应用弧度制下的弧长公式和扇形面积公式.问题导学1.度量角的单位制
(1)角度制
用 作为单位来度量角的单位制叫做角度制,规定1度的角等于周角的 .
(2)弧度制
①弧度制的定义
长度等于 的弧所对的圆心角叫做1弧度的角,用符号rad表示,读作弧度.以 作为单位来度量角的单位制叫做弧度制.度半径长弧度②任意角的弧度数与实数的对应关系
正角的弧度数是一个 ;负角的弧度数是一个 ;零角的弧度数是 .
③角的弧度数的计算
如果半径为r的圆的圆心角α所对弧的长为l,那么,角α的弧度数的绝对值是|α|= .正数负数零2.角度制与弧度制的换算
(1)2π360°π180°(2)一些特殊角的度数与弧度数的对应关系3.扇形的弧长及面积公式
设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则??题型探究思考1 1弧度的角是怎样规定的?1弧度的角和圆半径的大小有关吗?你能作出一个1弧度的角吗?
答 把长度等于半径长的弧所对的圆心角叫做1
弧度的角.1弧度的角是一个定值,与所在圆的半
径无关.如图所示,∠AOB就是1弧度的角.思考2 如果一个半径为r的圆的圆心角α所对的弧长是l,那么α的弧度数与l、r之间有着怎样的关系?请你完成下表,找出某种规律. 00°-90°π180°-2π-360°(?1°1-2反思及感悟小结 一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.如果半径为r的圆的圆心角α所对弧的长为l,那么,角α的弧度数的绝对值是|α|="l" /"r" .这里,α的正负由角α的终边的旋转方向决定.思考3 角度制与弧度制换算时,灵活运用下表中的对应关系,请补充完整.2π360°π180°例1 (1)把67°30′化成弧度;反思及感悟将角度转化为弧度时,要把带有分、秒的部分化为度之后,牢记π rad=180°即可求解.把弧度转化为角度时,直接用弧度数乘以 即可.??288探究点二 弧度制下的弧长公式和扇形面积公式思考 我们已经学习过角度制下的弧长公式和扇形面积公式,请根据“一周角(即360°)的弧度数为2π”这一事实化简上述公式.(设半径为r,圆心角弧度数为α).例2 已知一扇形的周长为40 cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
解 设扇形的圆心角为θ,半径为r,弧长为l,面积为S,
则l+2r=40,∴l=40-2r.∴当半径r=10 cm时,扇形的面积最大,最大值为100 cm2,所以当扇形的圆心角为2 rad,半径为10 cm时,扇形的面积最大为100 cm2.反思及感悟灵活运用扇形弧长公式、面积公式列方程组求解是解决此类问题的关键,有时运用函数思想、转化思想解决扇形中的有关最值问题,将扇形面积表示为半径的函数,转化为r的二次函数的最值问题.?探究点三 利用弧度制表示终边相同的角导引 在弧度制下,与α终边相同的角连同α在内可以表示为2kπ+α(k∈Z),其中α的单位必须是弧度.
思考1 利用弧度制表示出终边落在坐标轴上的角的集合.思考2 利用弧度制表示出终边落在各个象限的角的集合.?解 (1)∵-1 500°=-1 800°+300°=-5×360°+300°.∴-4与2π-4终边相同,是第二象限角.跟踪训练3 (1)把-1 480°写成α+2kπ(k∈Z)的形式,其中0≤α<2π;(2)若β∈[-4π,0],且β与(1)中α的终边相同,求β.又β∈[-4 π ,0],达标检测1.时针经过一小时,时针转过了( )解析 时针经过一小时,转过-30°,B2.已知扇形的周长是6 cm,面积是2 cm2,则扇形的中心角的弧度数是( )
A.1 B.1或2 C.1或4 D.2或4
解析 设扇形半径为r,中心角弧度数为α,C3.已知两角的和是1弧度,两角的差是1°,则这两个角分别为__________________.
解析 设这两个角为α,β弧度,不妨设α>β,规律及方法1.角的概念推广后,在弧度制下,角的集合与实数集R之间建立起一一对应的关系:每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.3.在弧度制下,扇形的弧长公式及面积公式都得到了简化,具体应用时,要注意角的单位取弧度.
