人教A版高中数学必修四2.2.2 向量减法运算及其几何意义 课件(共16张PPT)
文档属性
| 名称 | 人教A版高中数学必修四2.2.2 向量减法运算及其几何意义 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 388.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-18 00:00:00 | ||
图片预览



文档简介
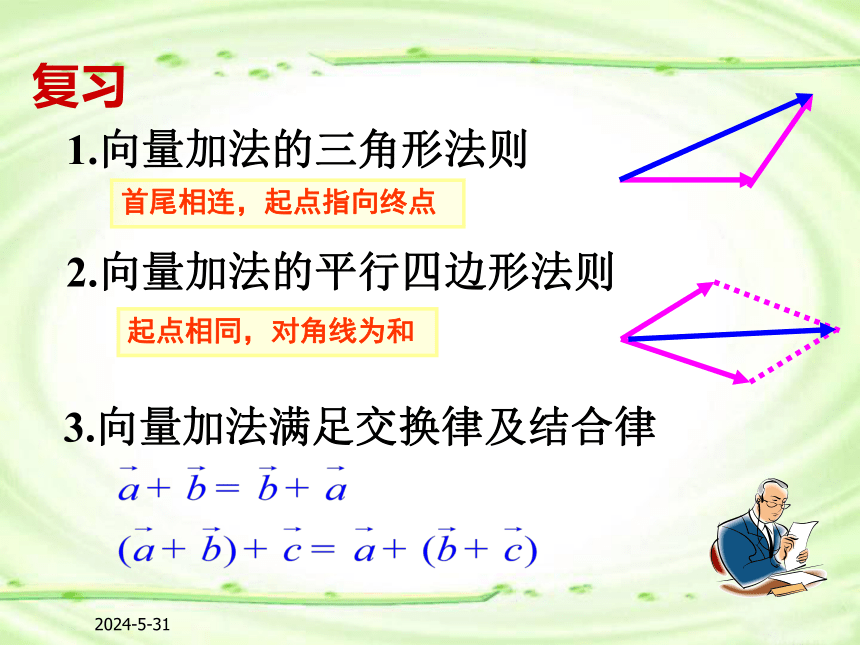
课件16张PPT。2020-4-172.2.2 向量减法运算及其几何意义2020-4-17复习1.向量加法的三角形法则2.向量加法的平行四边形法则 3.向量加法满足交换律及结合律首尾相连,起点指向终点起点相同,对角线为和2020-4-17结论:(2)零向量的相反向量仍是零向量,
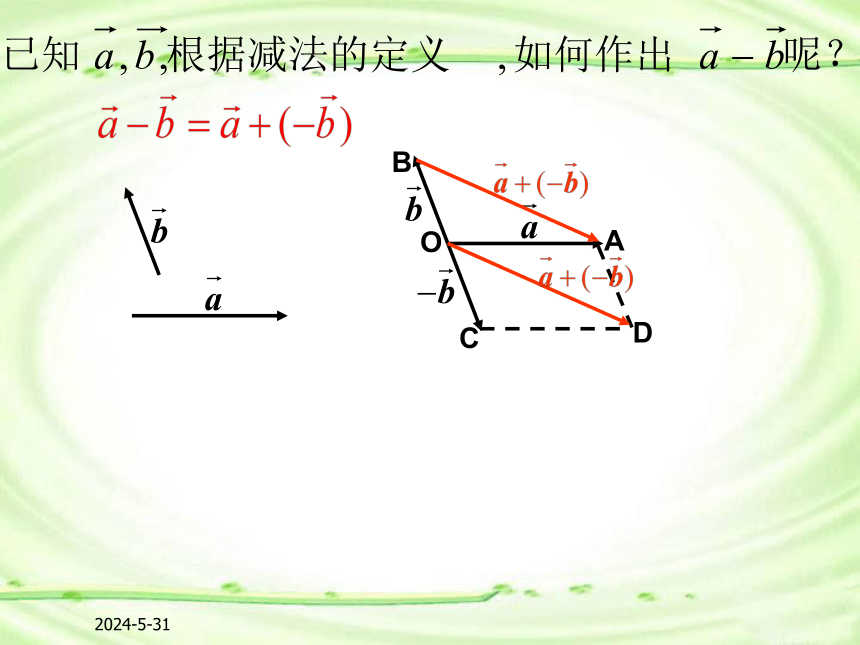
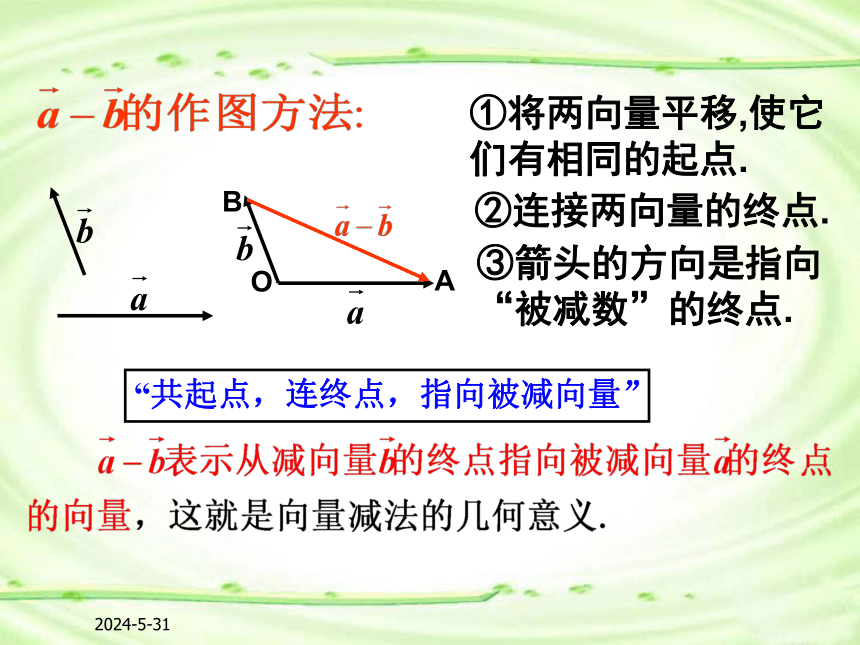
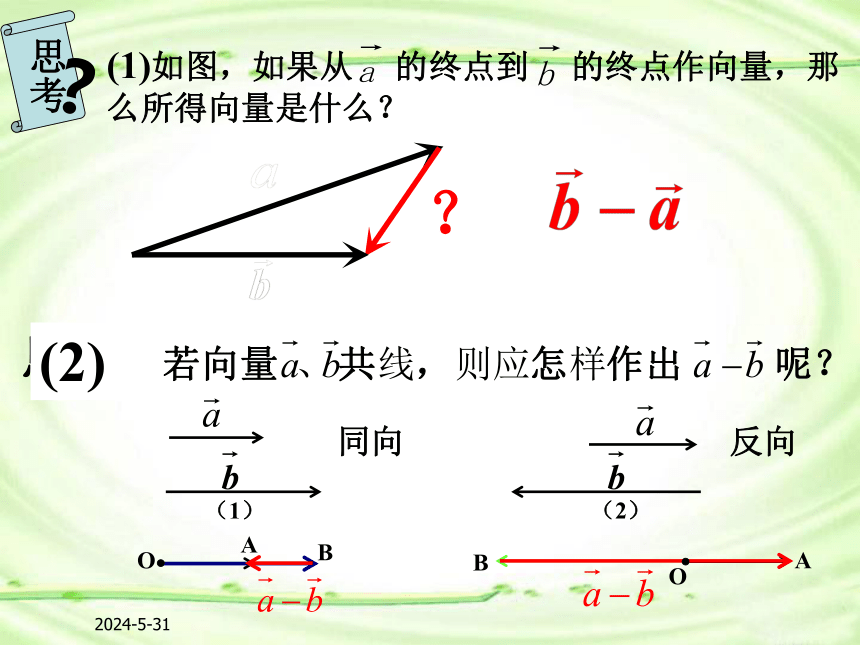
探究问题(一):相反向量的概念2020-4-171.定义:即:减去一个向量相当于加上这个向量的相反向量。2.向量减法的作图方法:探究问题(二):向量的减法2020-4-172020-4-17①将两向量平移,使它们有相同的起点.②连接两向量的终点.③箭头的方向是指向“被减数”的终点.“共起点,连终点,指向被减向量”2020-4-17?(1)如图,如果从 的终点到 的终点作向量,那么所得向量是什么?(1)(2)ABAB(2)同向反向2020-4-17探究问题(三):向量减法法则的应用2020-4-17练习
(1)(2)2020-4-17解:由向量加法的平行四边形法则,
得由向量的减法可得,2020-4-17不可能.因为平行四边形的两条对角线方向不同.2020-4-172020-4-17课后练习你能将减法运算转化为加法运算吗?2020-4-17练习22020-4-17练习3、判断下列命题是否正确,若不正确,说明理由3、相反向量就是方向相反的量4、若 ,则A、B、C
三点是一个三角形的顶点( )( )( )( )( )6、两个向量是互为相反向量,则两个向量共线( )√2020-4-171、向量的减法可以转化为向量的加法进行:
减去一个向量等于加上这个向量的相反向量.2、向量减法仍遵循三角形法则,它的规律是:
把两个向量平移到同一起点,再连结这两个向量的终点,则差向量的大小就是连结两终点的线段的长,方向指向被减向量的终点。“共起点,连终点,指向被减向量”3、在解题中要注意转化思想和数形结合思想的应用.
探究问题(一):相反向量的概念2020-4-171.定义:即:减去一个向量相当于加上这个向量的相反向量。2.向量减法的作图方法:探究问题(二):向量的减法2020-4-172020-4-17①将两向量平移,使它们有相同的起点.②连接两向量的终点.③箭头的方向是指向“被减数”的终点.“共起点,连终点,指向被减向量”2020-4-17?(1)如图,如果从 的终点到 的终点作向量,那么所得向量是什么?(1)(2)ABAB(2)同向反向2020-4-17探究问题(三):向量减法法则的应用2020-4-17练习
(1)(2)2020-4-17解:由向量加法的平行四边形法则,
得由向量的减法可得,2020-4-17不可能.因为平行四边形的两条对角线方向不同.2020-4-172020-4-17课后练习你能将减法运算转化为加法运算吗?2020-4-17练习22020-4-17练习3、判断下列命题是否正确,若不正确,说明理由3、相反向量就是方向相反的量4、若 ,则A、B、C
三点是一个三角形的顶点( )( )( )( )( )6、两个向量是互为相反向量,则两个向量共线( )√2020-4-171、向量的减法可以转化为向量的加法进行:
减去一个向量等于加上这个向量的相反向量.2、向量减法仍遵循三角形法则,它的规律是:
把两个向量平移到同一起点,再连结这两个向量的终点,则差向量的大小就是连结两终点的线段的长,方向指向被减向量的终点。“共起点,连终点,指向被减向量”3、在解题中要注意转化思想和数形结合思想的应用.
