1.3 三角函数的诱导公式(一)课件(共18张PPT)
文档属性
| 名称 | 1.3 三角函数的诱导公式(一)课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 712.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-18 18:52:10 | ||
图片预览






文档简介
课件18张PPT。§1.3 三角函数的诱导公式(一)学习目标1.了解三角函数的诱导公式的意义和作用.
2.理解诱导公式的推导过程.
3.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题.自主学习1.结合课本得到三个推到公式
2.理解公式的推到
3.用时10分钟设角α的终边与单位圆的交点为P,由三角函数定义知P点坐标为(cos α,sin α).
知识点一 诱导公式二角π+α的终边与角α的终边关于原点对称,角π+α的终边与单位圆的交点P1与P也关于原点对称,因此点P的坐标是(-cos α,-sin α),它们的三角函数关系如下:
诱导公式二sin(π+α)=-sin α,
cos(π+α)=-cos α,
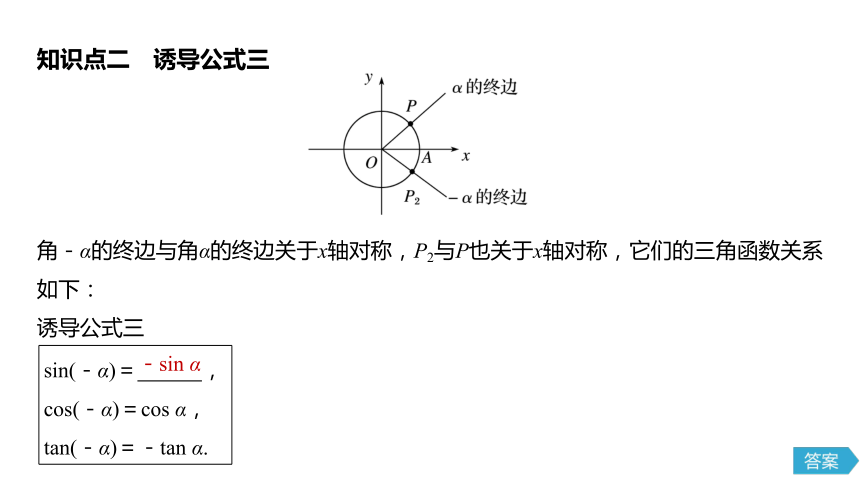
tan(π+α)=tan α.知识点二 诱导公式三角-α的终边与角α的终边关于x轴对称,P2与P也关于x轴对称,它们的三角函数关系如下:
诱导公式三sin(-α)= ,
cos(-α)=cos α,
tan(-α)=-tan α.-sin α知识点三 诱导公式四角π-α的终边与角α的终边关于y轴对称,P3与P也关于y轴对称,它们的三角函数关系如下:
诱导公式四sin(π-α)=sin α,
cos(π-α)=-cos α,
tan(π-α)= .-tan α公式一~四都叫做诱导公式,它们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数值与α的三角函数值之间的关系,这四组公式的共同特点是:
2kπ+α(k∈Z),π+α,-α,π-α的三角函数值等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.简记为“函数名不变,符号看象限”.1.诱导公式中角α是任意角.( )思考辨析 判断正误SI KAO BIAN XI PAN DUAN ZHENG WU×提示 正弦、余弦函数的诱导公式中,α为任意角,但是正切函数的诱导公式中,α的取值必须使公式中角的正切值有意义.2.sin(α-π)=sin α.( )×提示 sin(α-π)=sin[-(π-α)]=-sin(π-α)=-sin α.4.诱导公式对弧度制适用,对角度制不适用.( )×提示 在角度制和弧度制下,诱导公式都成立.√[基础自测]答案:B答案:A答案:-1[课堂探究]题型一 给角求值问题题型二 化简求值问题答案:1题型三 给值(或式)求值问题答案:D课堂小结sin(π+α)=-sin α,
cos(π+α)=-cos α,
tan(π+α)=tan α.sin(-α)= ,
cos(-α)=cos α,
tan(-α)=-tan α.sin(π-α)=sin α,
cos(π-α)=-cos α,
tan(π-α)= tan α .公式二公式三公式四作业 1.3.1 的对应练习题
2.理解诱导公式的推导过程.
3.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题.自主学习1.结合课本得到三个推到公式
2.理解公式的推到
3.用时10分钟设角α的终边与单位圆的交点为P,由三角函数定义知P点坐标为(cos α,sin α).
知识点一 诱导公式二角π+α的终边与角α的终边关于原点对称,角π+α的终边与单位圆的交点P1与P也关于原点对称,因此点P的坐标是(-cos α,-sin α),它们的三角函数关系如下:
诱导公式二sin(π+α)=-sin α,
cos(π+α)=-cos α,
tan(π+α)=tan α.知识点二 诱导公式三角-α的终边与角α的终边关于x轴对称,P2与P也关于x轴对称,它们的三角函数关系如下:
诱导公式三sin(-α)= ,
cos(-α)=cos α,
tan(-α)=-tan α.-sin α知识点三 诱导公式四角π-α的终边与角α的终边关于y轴对称,P3与P也关于y轴对称,它们的三角函数关系如下:
诱导公式四sin(π-α)=sin α,
cos(π-α)=-cos α,
tan(π-α)= .-tan α公式一~四都叫做诱导公式,它们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数值与α的三角函数值之间的关系,这四组公式的共同特点是:
2kπ+α(k∈Z),π+α,-α,π-α的三角函数值等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.简记为“函数名不变,符号看象限”.1.诱导公式中角α是任意角.( )思考辨析 判断正误SI KAO BIAN XI PAN DUAN ZHENG WU×提示 正弦、余弦函数的诱导公式中,α为任意角,但是正切函数的诱导公式中,α的取值必须使公式中角的正切值有意义.2.sin(α-π)=sin α.( )×提示 sin(α-π)=sin[-(π-α)]=-sin(π-α)=-sin α.4.诱导公式对弧度制适用,对角度制不适用.( )×提示 在角度制和弧度制下,诱导公式都成立.√[基础自测]答案:B答案:A答案:-1[课堂探究]题型一 给角求值问题题型二 化简求值问题答案:1题型三 给值(或式)求值问题答案:D课堂小结sin(π+α)=-sin α,
cos(π+α)=-cos α,
tan(π+α)=tan α.sin(-α)= ,
cos(-α)=cos α,
tan(-α)=-tan α.sin(π-α)=sin α,
cos(π-α)=-cos α,
tan(π-α)= tan α .公式二公式三公式四作业 1.3.1 的对应练习题
