人教版数学八年级下册同步练习:18.2.1矩形的性质与判定( 含详细答案)
文档属性
| 名称 | 人教版数学八年级下册同步练习:18.2.1矩形的性质与判定( 含详细答案) |  | |
| 格式 | zip | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 23:06:06 | ||
图片预览


文档简介
八年级下册同步练习:18.2.1矩形的性质与判定
一.选择题(共7小题)
1.检查一个门框(已知两组对边分别相等)是不是矩形,不可用的方法是( )
A.测量两条对角线是否相等
B.用重锤线检查竖门框是否与地面垂直
C.测量两条对角线是否互相平分
D.测量门框的三个角是否都是直角
2.如图,用一根绳子检查一个书架的侧边是否和上、下底都垂直,只需要用绳子分别测量比较书架的两条对角线AC,BD就可以判断,其数学依据是( )
A.三个角都是直角的四边形是矩形
B.对角线互相平分的四边形是平行四边形
C.对角线相等的平行四边形是矩形
D.对角线互相垂直平分的四边形是菱形
3.如图,在矩形ABCD中,AB>BC,点E,F,G,H分别是边DA,AB,BC,CD的中点,连接EG,HF,则图中矩形的个数共有( )
A.5个 B.8个 C.9个 D.11个
4.在矩形ABCD中,对角线AC=10cm,AB:BC=4:3,则它的周长为( )cm.
A.14 B.20 C.28 D.30
5.如图,在?ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=55°,则∠OAB的度数为( )
A.35° B.40° C.45° D.50°
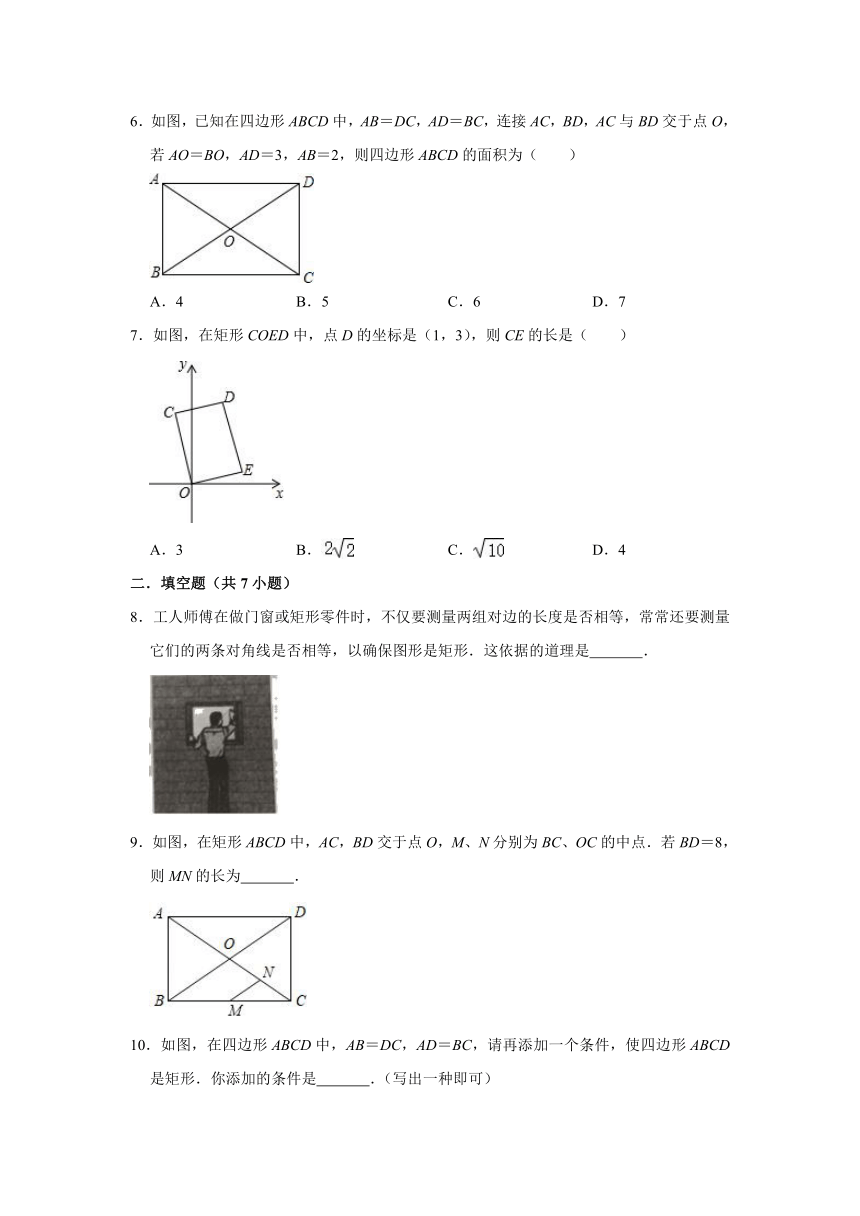
6.如图,已知在四边形ABCD中,AB=DC,AD=BC,连接AC,BD,AC与BD交于点O,若AO=BO,AD=3,AB=2,则四边形ABCD的面积为( )
A.4 B.5 C.6 D.7
7.如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )
A.3 B. C. D.4
二.填空题(共7小题)
8.工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形.这依据的道理是 .
9.如图,在矩形ABCD中,AC,BD交于点O,M、N分别为BC、OC的中点.若BD=8,则MN的长为 .
10.如图,在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD是矩形.你添加的条件是 .(写出一种即可)
11.如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n= 时,四边形ABEC是矩形.
12.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,若矩形ABCD的面积是12,那么阴影部分的面积是 .
13.如图,四边形ABDE是长方形,AC⊥DC于点C,交BD于点F,AE=AC,∠ADE=62°,则∠BAF的度数为 .
14.如图,矩形ABCD中,直线MN垂直平分AC,与CD,AB分别交于点M,N.若DM=2,CM=3,则矩形的对角线AC的长为 .
三.解答题(共6小题)
15.矩形ABCD中,AE平分∠BAD交BC于点E,CF平分∠BCD交AD于点F,
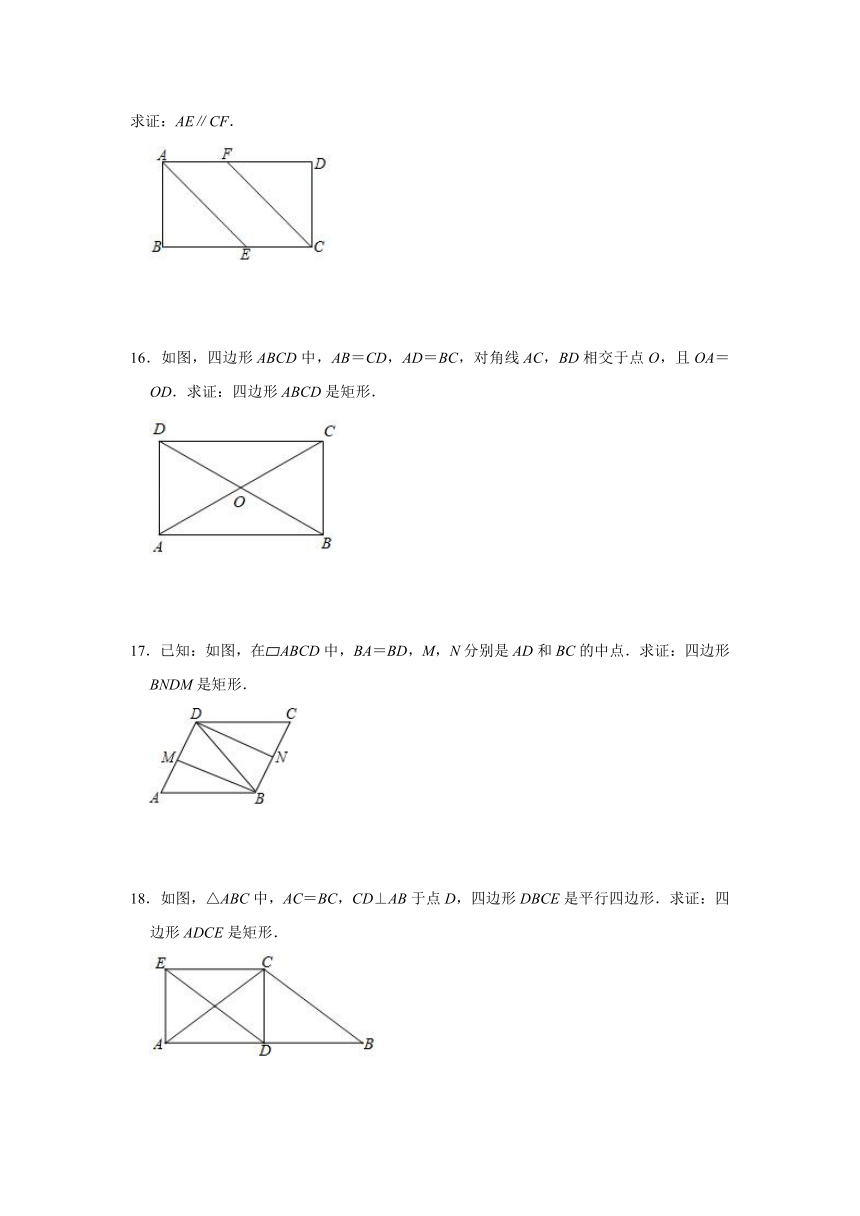
求证:AE∥CF.
16.如图,四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.
17.已知:如图,在?ABCD中,BA=BD,M,N分别是AD和BC的中点.求证:四边形BNDM是矩形.
18.如图,△ABC中,AC=BC,CD⊥AB于点D,四边形DBCE是平行四边形.求证:四边形ADCE是矩形.
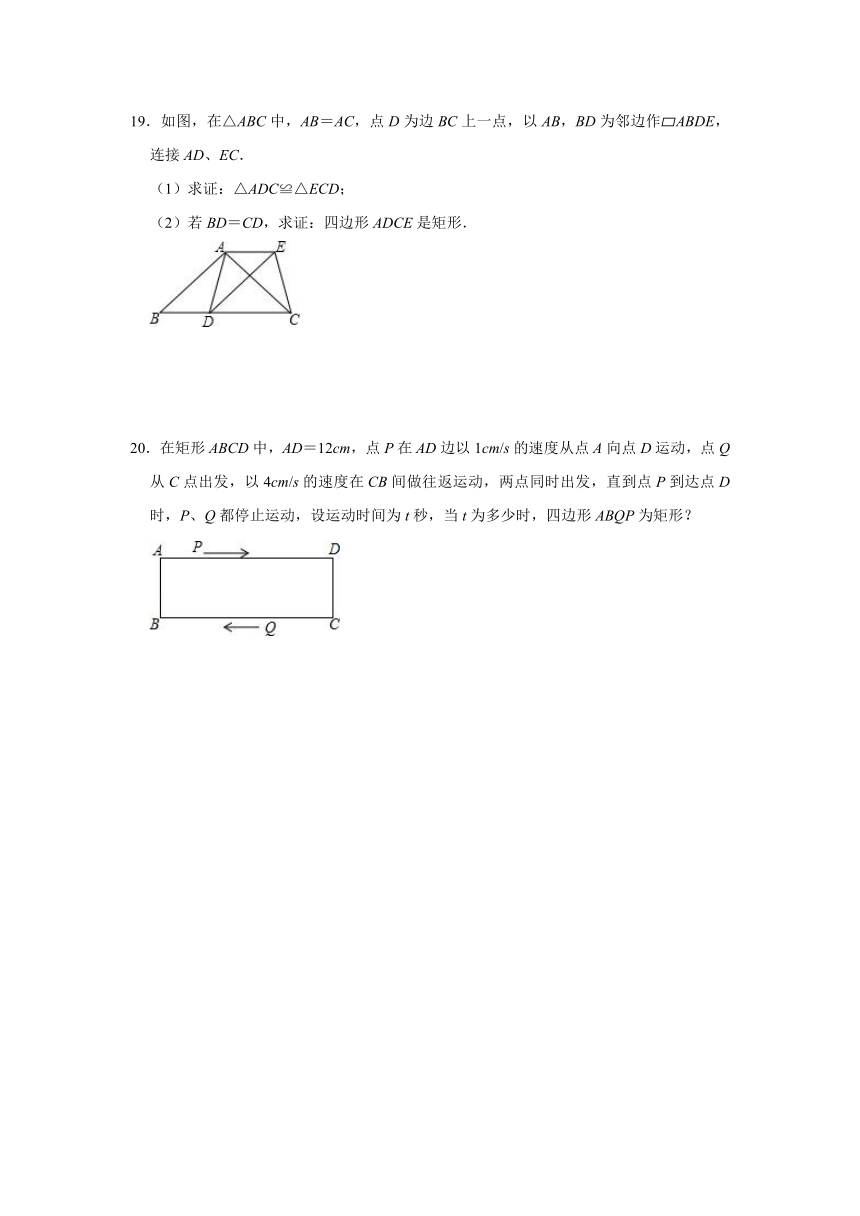
19.如图,在△ABC中,AB=AC,点D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD、EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
20.在矩形ABCD中,AD=12cm,点P在AD边以1cm/s的速度从点A向点D运动,点Q从C点出发,以4cm/s的速度在CB间做往返运动,两点同时出发,直到点P到达点D时,P、Q都停止运动,设运动时间为t秒,当t为多少时,四边形ABQP为矩形?
参考答案
一.选择题(共7小题)
1.【解答】解:∵门框两组对边分别相等,
∴门框是个平行四边形,
∵对角线相等的平行四边形是矩形,
故A不符合题意;
∵竖门框与地面垂直,门框一定是矩形;
故B不符合题意,
∵对角线互相平分的四边形是平行四边形,
∴C符合题意,
∵三个角都是直角的四边形是矩形,
故D不符合题意;
故选:C.
2.【解答】解:这种做法的依据是对角线相等的平行四边形为矩形,
故选:C.
3.【解答】解:∵E,G分别是边DA,BC的中点,四边形ABCD是矩形,
∴四边形DEGC、AEGB是矩形,
同理四边形ADHF、BCHF是矩形,
则图中四个小四边形是矩形,
故图中矩形的个数共有9个,
故选:C.
4.【解答】解:设AB=4xcm,则BC=3xcm,
∵四边形ABCD是矩形,
∴∠B=90°,AB=CD,AD=BC,
∴AC===5x(cm),
∴5x=10cm,
∴x=2cm,
∴AB=8cm,BC=6cm,
∴矩形ABCD的周长=2(8+6)=28(cm),
故选:C.
5.【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠DAB=90°,
∵∠OAD=55°,
∴∠OAB=∠DAB﹣∠OAD=35°
故选:A.
6.【解答】解:∵AB=DC,AD=BC,
∴四边形ABCD为平行四边形,
∴AO=OC,BO=DO,
∵AO=BO,
∴AC=BD,
∴四边形ABCD为矩形,
∵AD=3,AB=2,
∴四边形ABCD的面积为:AD?AB=2×3=6,
故选:C.
7.【解答】解:∵四边形COED是矩形,
∴CE=OD,
∵点D的坐标是(1,3),
∴OD==,
∴CE=,
故选:C.
二.填空题(共7小题)
8.【解答】解:因为门窗所构成的形状是矩形,
所以根据矩形的判定(对角线相等的平行四边形为矩形)可得出.
故答案为:对角线相等的平行四边形是矩形.
9.【解答】解:如图,∵四边形ABCD是矩形,AC,BD交于点O,BD=8
∴BD=2BO,即2BO=8.
∴BO=4.
又∵M、N分别为BC、OC的中点,
∴MN是△CBO的中位线,
∴MN=BO=2.
故答案是:2.
10.【解答】解:若四边形ABCD的对角线相等,
则由AB=DC,AD=BC可得.
△ABD≌△BAC≌△DAC≌△CDB,
所以四边形ABCD的四个内角相等分别等于90°即直角,
所以四边形ABCD是矩形,
故答案为:对角线相等(答案不唯一).
11.【解答】解:当∠AFC=2∠D时,四边形ABEC是矩形.
∵四边形ABCD是平行四边形,
∴BC∥AD,∠BCE=∠D,
由题意易得AB∥EC,AB=EC,
∴四边形ABEC是平行四边形.
∵∠AFC=∠FEC+∠BCE,
∴当∠AFC=2∠D时,则有∠FEC=∠FCE,
∴FC=FE,
∴四边形ABEC是矩形,
故答案为:2.
12.【解答】解:∵四边形ABCD是矩形,
∴AB∥CD,OA=OC,
∴∠EAO=∠FCO,
在△AOE和△COF中,,
∴△AOE≌△COF(ASA),
∴S△AOE=S△COF,
∴S阴=S△COD=S矩形ABCD=3,
故答案为:3.
13.【解答】解:∵四边形ABDE是矩形,
∴∠BAE=∠E=90°,
∵∠ADE=62°,
∴∠EAD=28°,
∵AC⊥CD,
∴∠C=∠E=90°
∵AE=AC,AD=AD,
∴Rt△ACD≌Rt△AED(HL)
∴∠EAD=∠CAD=28°,
∴∠BAF=90°﹣28°﹣28°=34°,
故答案为:34°.
14.【解答】解:如图,连接AM.
∵直线MN垂直平分AC,
∴MA=MC=3,
∵四边形ABCD是矩形,
∴∠D=90°,
∵DM=2,MA=3,
∴AD2=AM2﹣DM2=32﹣22=5,
∴AC===;
故答案为:.
三.解答题(共6小题)
15.【解答】证明:∵四边形ABCD是矩形,
∴AD∥BC,∠BAD=∠BCD=90°,
∴∠AEB=∠DAE,
∵AE平分∠BAD,CF平分∠BCD,
∴∠DAE=∠BAD=45°,∠BCF=∠BCD=45°,
∴∠AEB=∠DAE=∠BCF,
∴AE∥CF.
16.【解答】证明;∵四边形ABCD中,AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AC=2AO,BD=2OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形.
17.【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,BA=DC,
∵BA=BD,
∴BA=BD=DC,
∵M、N分别是AD和BC的中点,
∴BM⊥AD,DM=AD,BN=BC,
∴DM=BN,
又∵DM∥BN,
∴四边形BMDN是平行四边形,
∵BM⊥AD,
∴∠BMD=90°,
∴四边形BMDN是矩形.
18.【解答】证明:∵AC=BC,CD⊥AB,
∴∠ADC=90°,AD=BD.
∵在?DBCE中,EC∥BD,EC=BD,
∴EC∥AD,EC=AD.
∴四边形ADCE是平行四边形.
又∵∠ADC=90°,
∴四边形ADCE是矩形.
19.【解答】证明:(1)∵四边形ABDE是平行四边形(已知),
∴AB∥DE,AB=DE(平行四边形的对边平行且相等);
∴∠B=∠EDC(两直线平行,同位角相等);
又∵AB=AC(已知),
∴AC=DE(等量代换),∠B=∠ACB(等边对等角),
∴∠EDC=∠ACD(等量代换);
∵在△ADC和△ECD中,
,
∴△ADC≌△ECD(SAS);
(2)∵四边形ABDE是平行四边形(已知),
∴BD∥AE,BD=AE(平行四边形的对边平行且相等),
∴AE∥CD;
又∵BD=CD,
∴AE=CD(等量代换),
∴四边形ADCE是平行四边形(对边平行且相等的四边形是平行四边形);
在△ABC中,AB=AC,BD=CD,
∴AD⊥BC(等腰三角形的“三合一”性质),
∴∠ADC=90°,
∴?ADCE是矩形.
20.【解答】解:∵在矩形ABCD中,AD=12cm,
∴AD=BC=12cm.
当四边形ABQP为矩形时,AP=BQ.
①当0<t<3时,t=12﹣4t,
解得,t=;
②当3≤t<6时,t=4t﹣12,
解得 t=4;
③当6≤t<9时,t=36﹣4t,
解得 t=;
④当9≤t≤12时,t=4t﹣36,
解得,t=12.
综上所述,当t为或4或或12时,四边形ABQP为矩形.
