2.2.3 向量的数乘运算件(共38张PPT)
文档属性
| 名称 | 2.2.3 向量的数乘运算件(共38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 876.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-18 18:50:32 | ||
图片预览








文档简介
课件38张PPT。必修 四第二章
平面向量
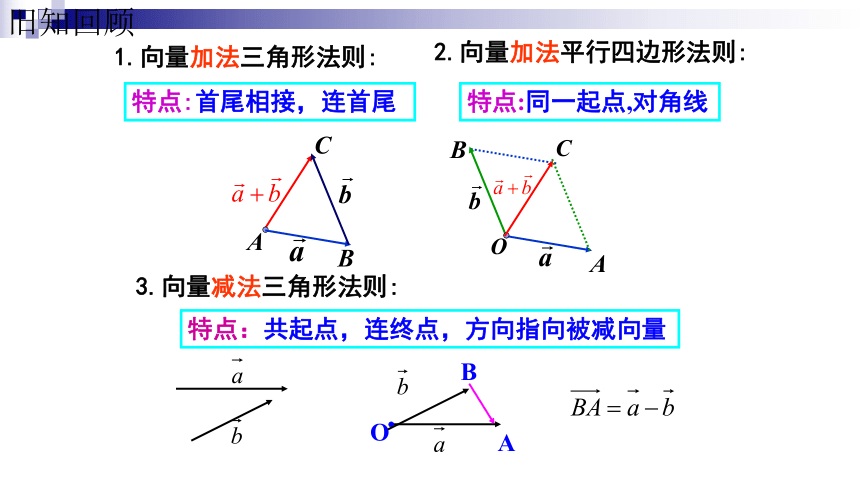
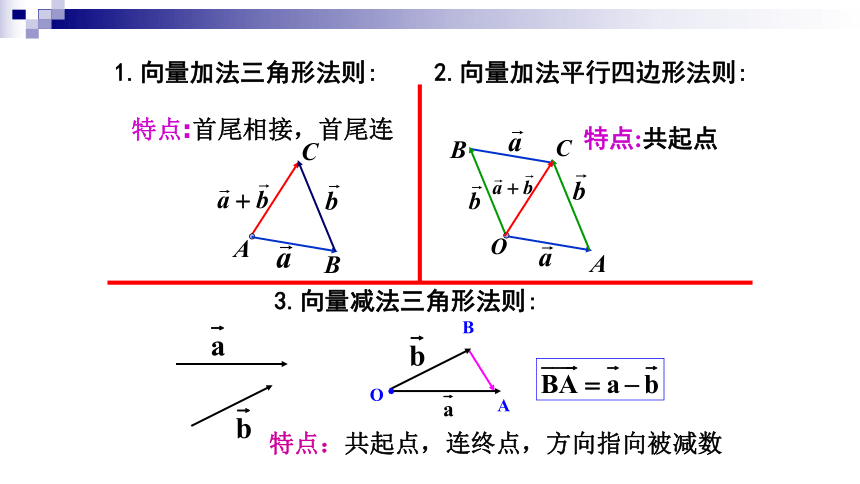
及其应用2.2.3向量的数乘运算 特点:共起点,连终点,方向指向被减向量1.向量加法三角形法则:特点:首尾相接,连首尾特点:同一起点,对角线2.向量加法平行四边形法则:3.向量减法三角形法则:旧知回顾1.向量加法三角形法则:特点:首尾相接,首尾连特点:共起点特点:共起点,连终点,方向指向被减数2.向量加法平行四边形法则:3.向量减法三角形法则:实际背景讲授新课即:一、向量的数乘运算的定义:注意:比较两个向量时,主要看它们的长度和方向二、数乘向量的几何意义数乘向量的几何意义就是把向量 沿 的方向或反
方向放大或缩短.若 ,当 沿 的方
向放大了 倍.当 沿 的方向缩短了 倍.
当 ,沿 的反方向放大了 倍.当
沿 的反方向缩短了 倍.由其几何意义可以看出
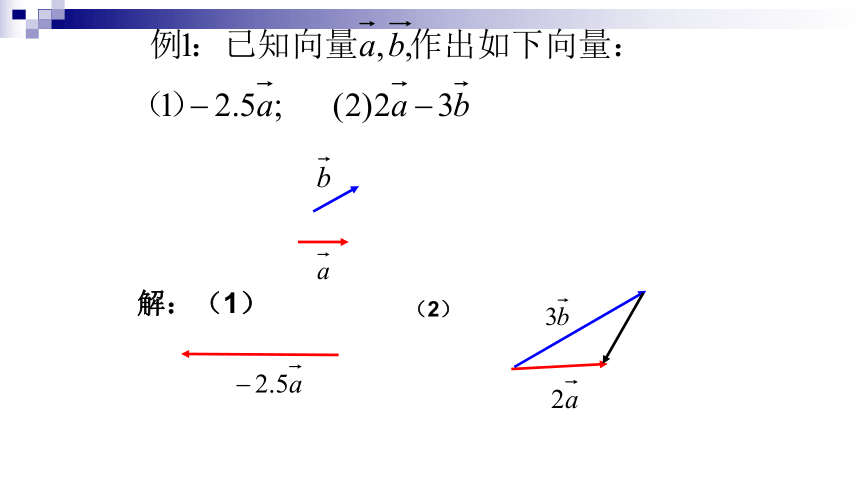
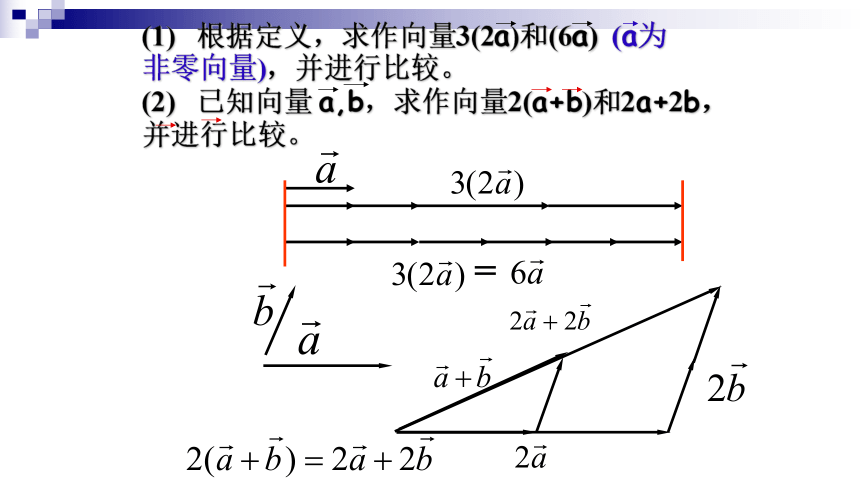
用数乘向量能解决几何中的相似问题.解:(1)(2)(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。(2) 已知向量 a,b,求作向量2(a+b)和2a+2b,并进行比较。三、向量的数乘运算满足如下运算律:向量的加、减、数乘运算统称为向量的线性运算例2:计算下列各式共线向量的充要条件:向量共线定理:1.把下列各小题中得向量b表示为实数与向量a得积.练习:2.判断下列各小题中的向量a与b是否共线.练习:例3.设AB=2(a+5b),BC= ?2a + 8b,CD=3(a ?b),
求证:A、B、D 三点共线。 分析要证A、B、D三点共线,可证AB=λBD关键是找到λ解:∵BD=BC+CD= ?2a + 8b+ 3(a ?b)=a+5b∴AB=2 BD∴ A、B、D 三点共线 向量 与非零向量 共线
有且仅有一个实数 ,使得 .定理 向量 与非零向量 共线
有且仅有一个实数 ,使得 .定理解:作图如右O依图猜想:A、B、C三点共线∴ A、B、C三点共线.练习例7:若
其中 , 是已知向量,求 ,分析:此题可把已知条件看作向量的方程,通过解方程组获得解:记 ①, ②例8. 在 中,设D为边BC的中点,求证:解:因为则四边形ABEC是平行四边形,D是BC中点,则D也是AE中点.由向量加法平行四边形法则有解2:例8. 在 中,设D为边BC的中点,求证:例8. 在 中,设D为边BC的中点,求证:解:(2)所以,所证等式成立练习: 如图,在 中,延长BA到C,使AC=BA,在OB上取
点D,使BD= OB.DC与OA交于E,设 请用
.解:因为A是BC的中点,所以 基础知识反馈C.A.B.(2).设 是非零向量, 是非零实数,下列结论正确的是( ).D.(1).下列四个说法正确的个数有( ).B.2个A.1个C.3个D.4个BC练习( C )分析:由 所以 在平行四边形ABCD中, ,M为BC的
中点,则 等于______ (1)(2)ABCD课堂小结:向量与平面几何CC四边形ABCD是菱形四边形ABCD是矩形对于任意一个三角形,
三角形的三条高的交点叫做垂心,
三角形的三条中线的交点所为重心,
三角形的三条角平分线的交点叫内心,
三角形的三条中垂线的交点叫外心 向量与三角形的“心”: ODMOM外心重心重心通过三角形ABC的_________内心例1,λ∈[0,+∞),则 P 的轨迹一定通过 △ABC 的( ) A.外心 B.内心C.重心 D.垂心B例2.又λ∈[0,+∞) 因此点 P 一定通过 ΔABC 的内心. ∴ 选(B)∴谢谢观看
平面向量
及其应用2.2.3向量的数乘运算 特点:共起点,连终点,方向指向被减向量1.向量加法三角形法则:特点:首尾相接,连首尾特点:同一起点,对角线2.向量加法平行四边形法则:3.向量减法三角形法则:旧知回顾1.向量加法三角形法则:特点:首尾相接,首尾连特点:共起点特点:共起点,连终点,方向指向被减数2.向量加法平行四边形法则:3.向量减法三角形法则:实际背景讲授新课即:一、向量的数乘运算的定义:注意:比较两个向量时,主要看它们的长度和方向二、数乘向量的几何意义数乘向量的几何意义就是把向量 沿 的方向或反
方向放大或缩短.若 ,当 沿 的方
向放大了 倍.当 沿 的方向缩短了 倍.
当 ,沿 的反方向放大了 倍.当
沿 的反方向缩短了 倍.由其几何意义可以看出
用数乘向量能解决几何中的相似问题.解:(1)(2)(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。(2) 已知向量 a,b,求作向量2(a+b)和2a+2b,并进行比较。三、向量的数乘运算满足如下运算律:向量的加、减、数乘运算统称为向量的线性运算例2:计算下列各式共线向量的充要条件:向量共线定理:1.把下列各小题中得向量b表示为实数与向量a得积.练习:2.判断下列各小题中的向量a与b是否共线.练习:例3.设AB=2(a+5b),BC= ?2a + 8b,CD=3(a ?b),
求证:A、B、D 三点共线。 分析要证A、B、D三点共线,可证AB=λBD关键是找到λ解:∵BD=BC+CD= ?2a + 8b+ 3(a ?b)=a+5b∴AB=2 BD∴ A、B、D 三点共线 向量 与非零向量 共线
有且仅有一个实数 ,使得 .定理 向量 与非零向量 共线
有且仅有一个实数 ,使得 .定理解:作图如右O依图猜想:A、B、C三点共线∴ A、B、C三点共线.练习例7:若
其中 , 是已知向量,求 ,分析:此题可把已知条件看作向量的方程,通过解方程组获得解:记 ①, ②例8. 在 中,设D为边BC的中点,求证:解:因为则四边形ABEC是平行四边形,D是BC中点,则D也是AE中点.由向量加法平行四边形法则有解2:例8. 在 中,设D为边BC的中点,求证:例8. 在 中,设D为边BC的中点,求证:解:(2)所以,所证等式成立练习: 如图,在 中,延长BA到C,使AC=BA,在OB上取
点D,使BD= OB.DC与OA交于E,设 请用
.解:因为A是BC的中点,所以 基础知识反馈C.A.B.(2).设 是非零向量, 是非零实数,下列结论正确的是( ).D.(1).下列四个说法正确的个数有( ).B.2个A.1个C.3个D.4个BC练习( C )分析:由 所以 在平行四边形ABCD中, ,M为BC的
中点,则 等于______ (1)(2)ABCD课堂小结:向量与平面几何CC四边形ABCD是菱形四边形ABCD是矩形对于任意一个三角形,
三角形的三条高的交点叫做垂心,
三角形的三条中线的交点所为重心,
三角形的三条角平分线的交点叫内心,
三角形的三条中垂线的交点叫外心 向量与三角形的“心”: ODMOM外心重心重心通过三角形ABC的_________内心例1,λ∈[0,+∞),则 P 的轨迹一定通过 △ABC 的( ) A.外心 B.内心C.重心 D.垂心B例2.又λ∈[0,+∞) 因此点 P 一定通过 ΔABC 的内心. ∴ 选(B)∴谢谢观看
