1.4.2正弦函数、余弦函数的性质---周期性公开课教学课件 (共24张PPT)
文档属性
| 名称 | 1.4.2正弦函数、余弦函数的性质---周期性公开课教学课件 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-18 18:45:59 | ||
图片预览






文档简介
课件24张PPT。yOx普通高中课程标准实验教科书(人教A版)数学4
?
正弦函数、余弦函数的性质-------周期性
1. 从生活实际的周期现象出发,概括抽象出周期函数的概念;
2. 运用数形结合方法探究正、余弦函数的周期性,从而进一步推导出正、余弦型函数的周期公式;
3. 会求一些简单三角函数的周期.
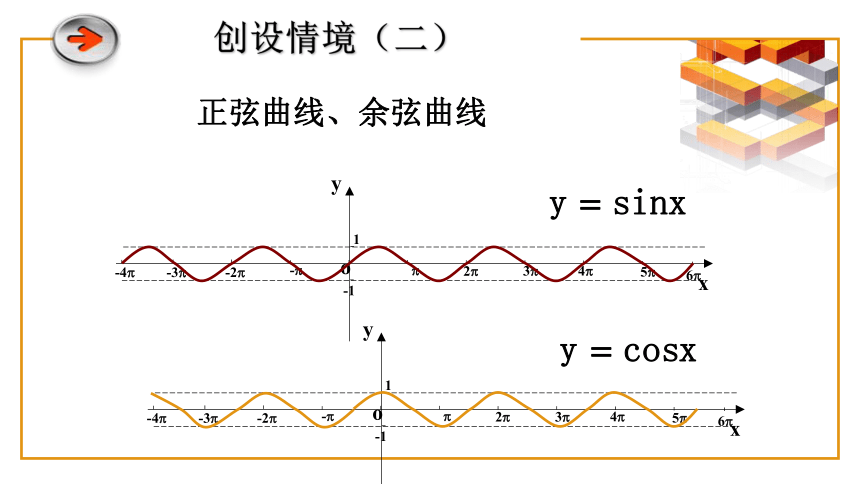
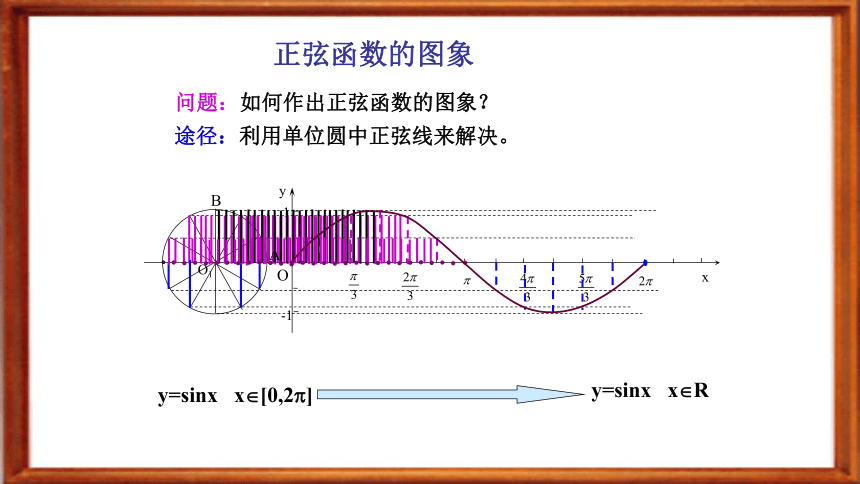
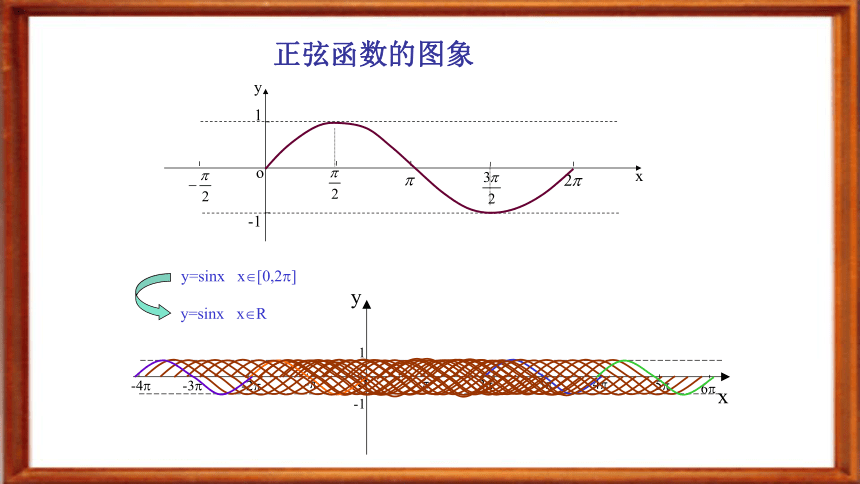
学习目标创设情境(一)★今天是星期四,再过几天又是星期四?换句话说,只要过的天数具有什么特征,就会再次出现星期四?正弦曲线、余弦曲线创设情境(二) 正弦函数的图象 问题:如何作出正弦函数的图象?途径:利用单位圆中正弦线来解决。 y=sinx x?[0,2?]y=sinx x?R AB 正弦函数的图象 y=sinx x?[0,2?]y=sinx x?Rsin(x+2k?)=sinx, k?Z建构概念终边相同角的三角函数值相等3问题探究11. 对于函数f(x),如果存在一个非零的常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数非零常数T叫做这个函数的周期建构概念??思考 ??问题探究21. 对于函数f(x),如果存在一个非零的常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数问题探究3 正弦函数y=sinx是周期函数吗?若是,周期是多少?2π、4π 、6π……-2π、-4π 、-6π ……
2kπ(k∈Z且K≠0)都是它的周期.2.对于一个周期函数f(x),如果在它所有的周 期中存在一个最小的正数,那么这个最小 的正数就叫做f(x)的最小正周期。
建构概念 正弦函数y=sinx是周期函数,周期是多少?正弦函数y=sinx的周期是2? 如果不加特别说明,我们谈到函数周期时,都是指最小正周期。知识探究 类比的方法,得到余弦函数y=cosx的周期性. 思考:是不是所有的周期函数都有最小正周期?余弦函数y=cosx是周期函数,周期是2?例1. 求下列函数的周期:知识应用我来当老师编题要求:以正、余弦型函数 y=Asin(ωx+φ) 及y=Acos(ωx+φ) (其中A ,ω,φ为常数,且 A≠0, ω≠0 )为模型编题.
思考:你能从上面的解答过程中归纳一下这些函数的周期与解析式中的哪些量有关系吗?
你能从上面的解答过程中归纳一下这些函数的周期与解析式中的哪些量有关系吗?周期知识探究
(小组合作)解:归纳总结当堂检测:求下列函数的周期: 一般地,函数 y=Asin(ωx+φ) 及y=Acos(ωx+φ) (其中A ,ω,φ为常数,且 A≠0, ω≠0 )的周期是:周期求法1.定义法:
2.公式法:3.图象法:1. 从生活实际的周期现象出发,概括抽象出周期函数的概念;
2. 运用数形结合方法探究正、余弦函数的周期性,从而进一步推导出正、余弦型函数的周期公式;
3. 会求一些简单三角函数的周期.
目标回顾课堂小结 本节课你在 上都有哪些收获?
知识?方法?思想 必做:P46 习题1.A组 第3题
B组 第3题
知者加速:探究正弦函数、余弦函数还有哪些性质?
课堂作业
?
正弦函数、余弦函数的性质-------周期性
1. 从生活实际的周期现象出发,概括抽象出周期函数的概念;
2. 运用数形结合方法探究正、余弦函数的周期性,从而进一步推导出正、余弦型函数的周期公式;
3. 会求一些简单三角函数的周期.
学习目标创设情境(一)★今天是星期四,再过几天又是星期四?换句话说,只要过的天数具有什么特征,就会再次出现星期四?正弦曲线、余弦曲线创设情境(二) 正弦函数的图象 问题:如何作出正弦函数的图象?途径:利用单位圆中正弦线来解决。 y=sinx x?[0,2?]y=sinx x?R AB 正弦函数的图象 y=sinx x?[0,2?]y=sinx x?Rsin(x+2k?)=sinx, k?Z建构概念终边相同角的三角函数值相等3问题探究11. 对于函数f(x),如果存在一个非零的常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数非零常数T叫做这个函数的周期建构概念??思考 ??问题探究21. 对于函数f(x),如果存在一个非零的常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数问题探究3 正弦函数y=sinx是周期函数吗?若是,周期是多少?2π、4π 、6π……-2π、-4π 、-6π ……
2kπ(k∈Z且K≠0)都是它的周期.2.对于一个周期函数f(x),如果在它所有的周 期中存在一个最小的正数,那么这个最小 的正数就叫做f(x)的最小正周期。
建构概念 正弦函数y=sinx是周期函数,周期是多少?正弦函数y=sinx的周期是2? 如果不加特别说明,我们谈到函数周期时,都是指最小正周期。知识探究 类比的方法,得到余弦函数y=cosx的周期性. 思考:是不是所有的周期函数都有最小正周期?余弦函数y=cosx是周期函数,周期是2?例1. 求下列函数的周期:知识应用我来当老师编题要求:以正、余弦型函数 y=Asin(ωx+φ) 及y=Acos(ωx+φ) (其中A ,ω,φ为常数,且 A≠0, ω≠0 )为模型编题.
思考:你能从上面的解答过程中归纳一下这些函数的周期与解析式中的哪些量有关系吗?
你能从上面的解答过程中归纳一下这些函数的周期与解析式中的哪些量有关系吗?周期知识探究
(小组合作)解:归纳总结当堂检测:求下列函数的周期: 一般地,函数 y=Asin(ωx+φ) 及y=Acos(ωx+φ) (其中A ,ω,φ为常数,且 A≠0, ω≠0 )的周期是:周期求法1.定义法:
2.公式法:3.图象法:1. 从生活实际的周期现象出发,概括抽象出周期函数的概念;
2. 运用数形结合方法探究正、余弦函数的周期性,从而进一步推导出正、余弦型函数的周期公式;
3. 会求一些简单三角函数的周期.
目标回顾课堂小结 本节课你在 上都有哪些收获?
知识?方法?思想 必做:P46 习题1.A组 第3题
B组 第3题
知者加速:探究正弦函数、余弦函数还有哪些性质?
课堂作业
