2.2.1向量的加法运算及其几何意义课件(共25张PPT)
文档属性
| 名称 | 2.2.1向量的加法运算及其几何意义课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-19 12:25:57 | ||
图片预览



文档简介
课件25张PPT。2.2 平面向量的线性运算
2.2.1向量加法运算及其几何意义
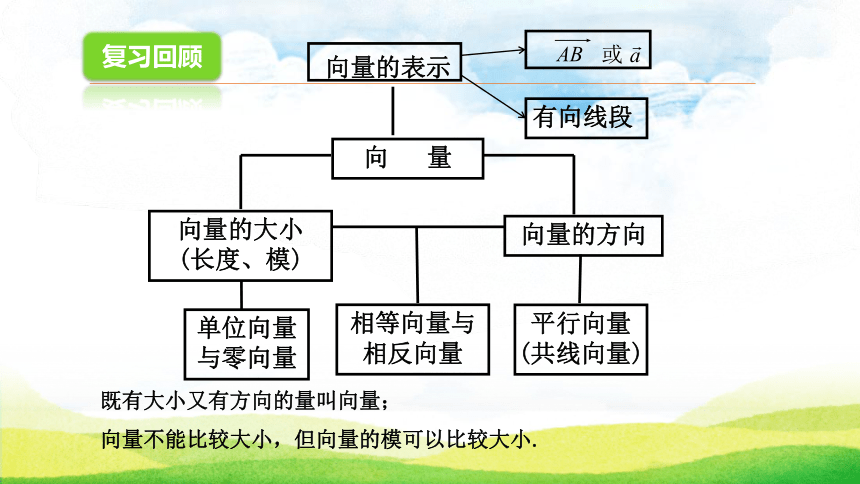
复习回顾既有大小又有方向的量叫向量;
向量不能比较大小,但向量的模可以比较大小.向 量 数能进行运算,因为有了运算而使数的威力无穷。与数的运算类比,向量是否也能进行运算呢? 今天我们学习向量的加法运算。 人们从向量的物理背景和数的运算中得到启发,引进了向量的运算。学习目标1.理解并掌握加法的概念,了解向量加法的物理意义及其几何意义.
2.掌握向量加法的三角形法则和平行四边形法则,并能熟练地运用这两个法则作两个向量的加法运算.
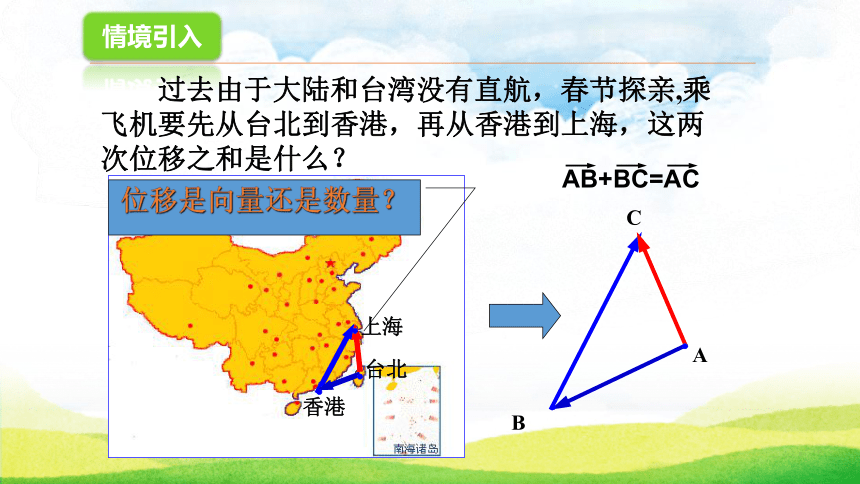
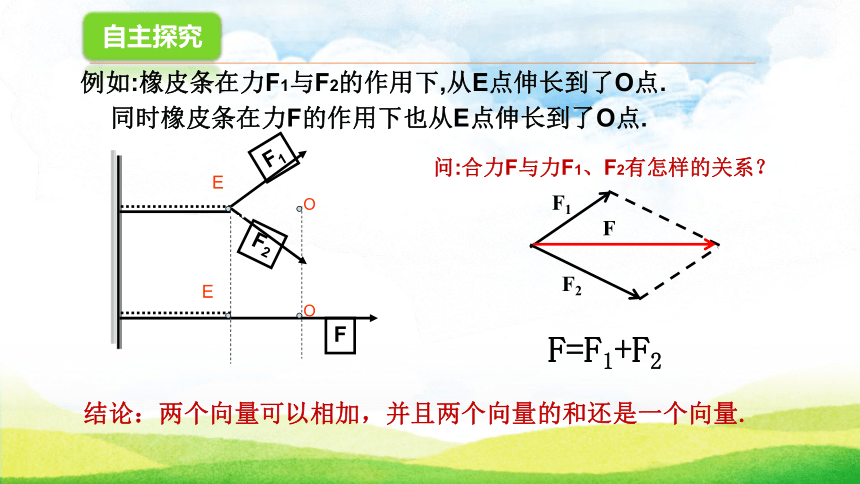
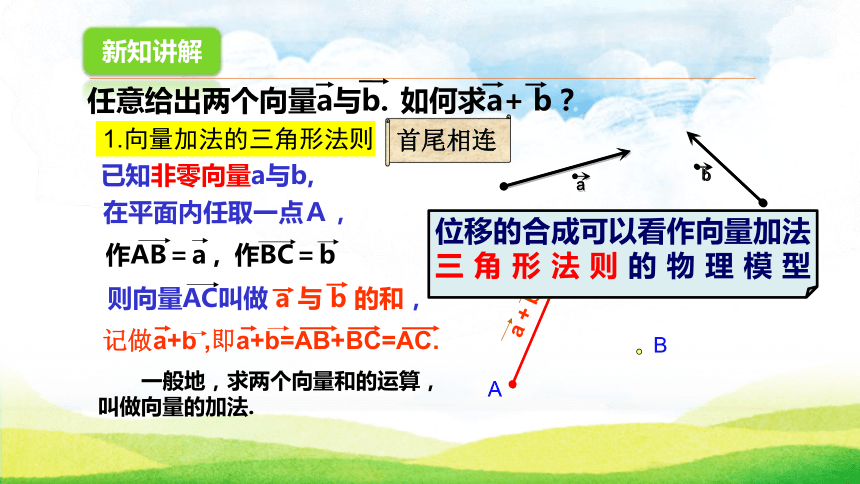
3.了解向量加法的交换律和结合律,并能依几何意义作图解释加法运算律的合理性.情境引入 过去由于大陆和台湾没有直航,春节探亲,乘飞机要先从台北到香港,再从香港到上海,这两次位移之和是什么?上海台北香港位移是向量还是数量?自主探究EOOE例如:橡皮条在力F1与F2的作用下,从E点伸长到了O点.同时橡皮条在力F的作用下也从E点伸长到了O点.问:合力F与力F1、F2有怎样的关系?F=F1+F2结论:两个向量可以相加,并且两个向量的和还是一个向量.新知讲解1.向量加法的三角形法则已知非零向量a与b,在平面内任取一点A,作AB=a , 作BC=b 则向量AC叫做 a 与 b 的和,记做a+b ,即a+b=AB+BC=AC.位移的合成可以看作向量加法三角形法则的物理模型首尾相连 一般地,求两个向量和的运算,
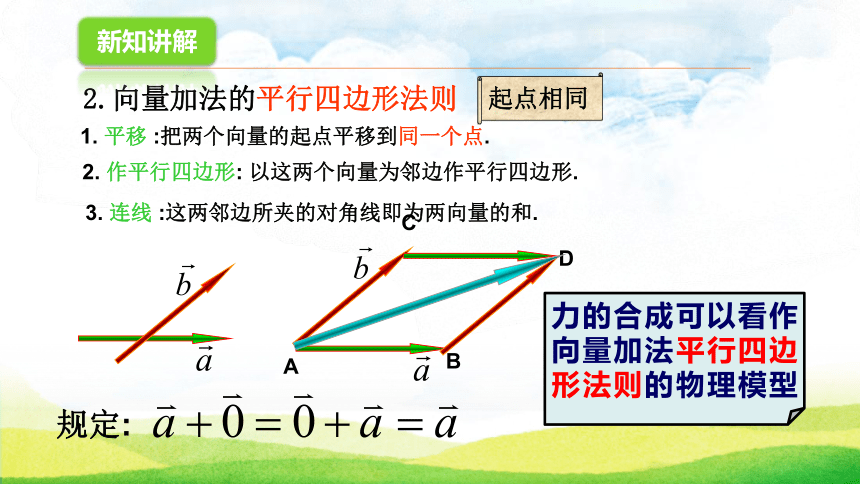
叫做向量的加法.2.向量加法的平行四边形法则1. 平移 :把两个向量的起点平移到同一个点.2. 作平行四边形: 以这两个向量为邻边作平行四边形.3. 连线 :这两邻边所夹的对角线即为两向量的和.新知讲解力的合成可以看作向量加法平行四边形法则的物理模型起点相同探究:求和时用三角形法则与平行四边形法则
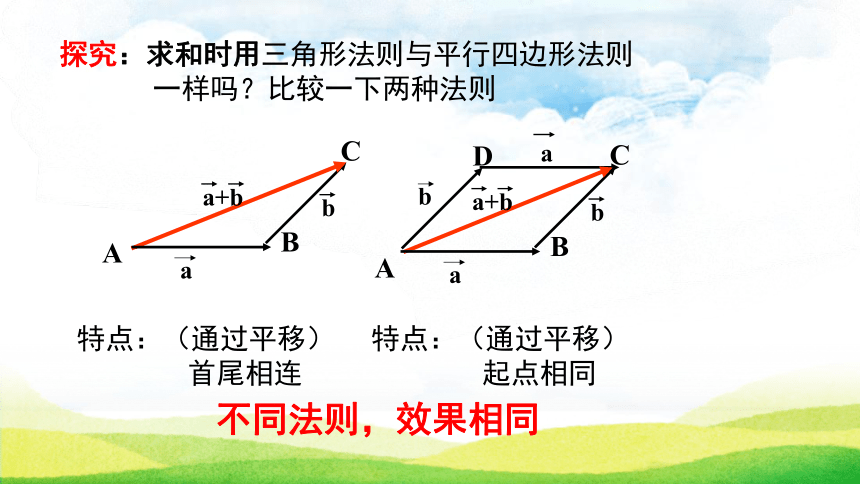
一样吗?比较一下两种法则特点:(通过平移)
首尾相连特点:(通过平移)
起点相同不同法则,效果相同典例剖析
则 三角形法则作法1:在平面内任取一点O,作法2:在平面内任取一点O,平行四边形法则随堂练习 已知向量 ,用向量加法的三角形法则和平行四边形法则作出① ② 独立思考请选用合适符号连接:?自主探究 任意向量 的加法是否也满足交换律和结合律??随堂练习ABCDE1. 根据图示填空:推广:典例剖析例2: 长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图所示,一艘船从长江南岸A点出发,以5km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度(保留两个有效数字)
(2)求船实际航行的速度的大小与方向(用与江水速度间的夹角表示,精确到度).
解:(1)C(1)试用向量表示江水速度、船速以及船实际航行的速度(保留两个有效数字)(2)求船实际航行的速度的大小与方向(用与江水速度间的夹角表示,精确到度).在Rt△ABC中,船实际航行速度大小约为5.4km/h,方向与水的流速间的夹角约为68°??达标检测1. 化简???????达标检测D达标检测5. 一艘船以5 km/h的速度向垂直于对岸方向行驶,船实际航行方向与水流方向成30°角,求水流速度和船实际速度.1.两个向量的和仍然是向量。 向量加法的三角形法则 以第一个向量的终点作为第二个向量的起点,则从第一个向量的起点到第二个向量的终点的向量就表示和向量.向量加法平行四边形法则以两个同一起点的向量为邻边作平行四边形, 以这两个向量的起点为起点的对角线所对应的向量就表示和向量.小结:2.向量加法法则:3.向量加法的运算律 (1)交换律:a+b=b+a. (2)结合律:(a+b)+c=a+(b+c).4.向量三角不等式:?谢谢大家祝同学们劳逸结合、学习愉快!2020年2月自主探究??1.向量的加法满足交换律吗?如何检验?自主探究ABCDbc ?2.向量的加法满足结合律吗?如何检验?
2.2.1向量加法运算及其几何意义
复习回顾既有大小又有方向的量叫向量;
向量不能比较大小,但向量的模可以比较大小.向 量 数能进行运算,因为有了运算而使数的威力无穷。与数的运算类比,向量是否也能进行运算呢? 今天我们学习向量的加法运算。 人们从向量的物理背景和数的运算中得到启发,引进了向量的运算。学习目标1.理解并掌握加法的概念,了解向量加法的物理意义及其几何意义.
2.掌握向量加法的三角形法则和平行四边形法则,并能熟练地运用这两个法则作两个向量的加法运算.
3.了解向量加法的交换律和结合律,并能依几何意义作图解释加法运算律的合理性.情境引入 过去由于大陆和台湾没有直航,春节探亲,乘飞机要先从台北到香港,再从香港到上海,这两次位移之和是什么?上海台北香港位移是向量还是数量?自主探究EOOE例如:橡皮条在力F1与F2的作用下,从E点伸长到了O点.同时橡皮条在力F的作用下也从E点伸长到了O点.问:合力F与力F1、F2有怎样的关系?F=F1+F2结论:两个向量可以相加,并且两个向量的和还是一个向量.新知讲解1.向量加法的三角形法则已知非零向量a与b,在平面内任取一点A,作AB=a , 作BC=b 则向量AC叫做 a 与 b 的和,记做a+b ,即a+b=AB+BC=AC.位移的合成可以看作向量加法三角形法则的物理模型首尾相连 一般地,求两个向量和的运算,
叫做向量的加法.2.向量加法的平行四边形法则1. 平移 :把两个向量的起点平移到同一个点.2. 作平行四边形: 以这两个向量为邻边作平行四边形.3. 连线 :这两邻边所夹的对角线即为两向量的和.新知讲解力的合成可以看作向量加法平行四边形法则的物理模型起点相同探究:求和时用三角形法则与平行四边形法则
一样吗?比较一下两种法则特点:(通过平移)
首尾相连特点:(通过平移)
起点相同不同法则,效果相同典例剖析
则 三角形法则作法1:在平面内任取一点O,作法2:在平面内任取一点O,平行四边形法则随堂练习 已知向量 ,用向量加法的三角形法则和平行四边形法则作出① ② 独立思考请选用合适符号连接:?自主探究 任意向量 的加法是否也满足交换律和结合律??随堂练习ABCDE1. 根据图示填空:推广:典例剖析例2: 长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图所示,一艘船从长江南岸A点出发,以5km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度(保留两个有效数字)
(2)求船实际航行的速度的大小与方向(用与江水速度间的夹角表示,精确到度).
解:(1)C(1)试用向量表示江水速度、船速以及船实际航行的速度(保留两个有效数字)(2)求船实际航行的速度的大小与方向(用与江水速度间的夹角表示,精确到度).在Rt△ABC中,船实际航行速度大小约为5.4km/h,方向与水的流速间的夹角约为68°??达标检测1. 化简???????达标检测D达标检测5. 一艘船以5 km/h的速度向垂直于对岸方向行驶,船实际航行方向与水流方向成30°角,求水流速度和船实际速度.1.两个向量的和仍然是向量。 向量加法的三角形法则 以第一个向量的终点作为第二个向量的起点,则从第一个向量的起点到第二个向量的终点的向量就表示和向量.向量加法平行四边形法则以两个同一起点的向量为邻边作平行四边形, 以这两个向量的起点为起点的对角线所对应的向量就表示和向量.小结:2.向量加法法则:3.向量加法的运算律 (1)交换律:a+b=b+a. (2)结合律:(a+b)+c=a+(b+c).4.向量三角不等式:?谢谢大家祝同学们劳逸结合、学习愉快!2020年2月自主探究??1.向量的加法满足交换律吗?如何检验?自主探究ABCDbc ?2.向量的加法满足结合律吗?如何检验?
