高一年级数学必修四(人教A版) 1.1.2《弧度制》第1课时 课件(共28张PPT)
文档属性
| 名称 | 高一年级数学必修四(人教A版) 1.1.2《弧度制》第1课时 课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-19 09:53:57 | ||
图片预览







文档简介
课件28张PPT。高一年级数学必修四(人教A版)
1.1.2《弧度制》第1课时 自我介绍 ?温故知新?2.弧长公式及扇形面积公式
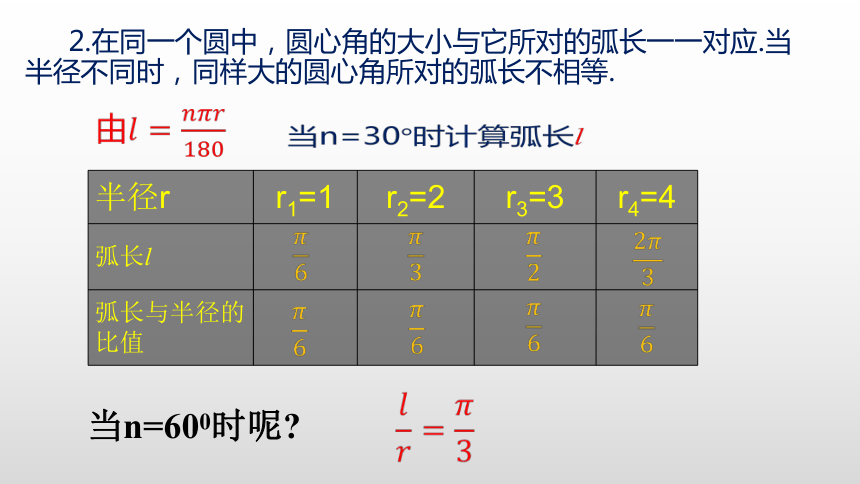
提出问题1.度量角的方法“度分秒制”:把圆周角分为360等份—>1度的角—>60等份—>1分的角—>60等份—>1秒的角.?????????当n=600时呢??2.在同一个圆中,圆心角的大小与它所对的弧长一一对应.当半径不同时,同样大的圆心角所对的弧长不相等.
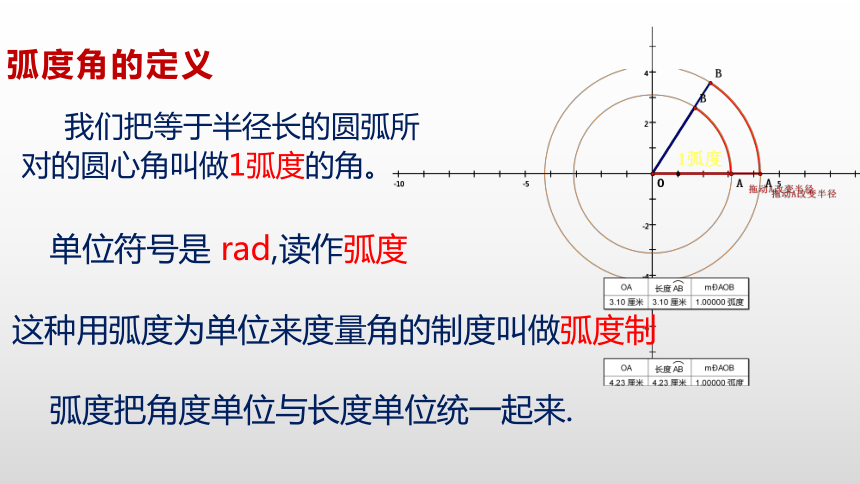
提出问题3、实验结果表明:当半径不同时,同样的圆心角所对的弧长与半径的比是常数.?称这个常数为该角的弧度数.能否用弧长来定义角的大小呢?我们把等于半径长的圆弧所对的圆心角叫做1弧度的角。单位符号是 rad,读作弧度弧度把角度单位与长度单位统一起来.弧度角的定义这种用弧度为单位来度量角的制度叫做弧度制思考:如果一个半径为r的圆的圆心角α所对的弧长是l,那么α的弧度数是多少? 如图:若圆的半径为2,圆心角∠AOB(正角)所对的圆弧长为4,那么 ∠AOB的弧度数就是24BoAα的正负由角α的终边旋转方向决定.?用“弧度”与“度”去度量每一个角时,除了零角以外,所得到的量数都是不同的,但它们既然是度量同一个角的结果,二者就可以相互换算. 若弧是一个整圆,它的圆心角是周角,其弧度数是2π,而在角度制里它是360°. 角度制与弧度制的换算 ∵ 360?=2? rad ,∴180?=? rad ??角度制与弧度制的换算写出一些特殊角的弧度数或角度 ??????????????课堂实例??课堂实例??1.把下列角的角度化为弧度?(1)36°=?????课堂练习12 °-1080 °?(2)210°=114°36'2.把下列角的弧度化为角度例3.用弧度制表示:
(1).终边在x轴上的角的集合
(2).终边在y轴上的角的集合
(3).终边在坐标轴上的角的集合
课堂实例????弧度制下的角与实数之间的关系是怎样的呢?弧度数用弧度来度量角,实际上角的集合与实数集R之间建立一 一对应的关系:正实数零负实数对应角的弧度数弧度数(1)都是度量角的大小的单位制
角度制的单位是“度”; (单位不能省略)
弧度制的单位是“弧度”; (单位可以省略)
?(4)两种单位制都与半径无关.角度制与弧度制(3)弧度制是十进制,它的表示是用一个实数表示,而角度制是六十进制; 1弧度≠1o课堂探究?弧长等于弧所对的圆心角(的弧度数)的绝对值与半径的积. 得到弧长公式:l=|α|·R??课堂探究表示的是在半径为R的圆中,弧长为l的弧所对的圆心角是αrad。l=|α|·R证明:设扇形所对的圆心角为no(αrad),则??课堂探究????课堂实例ABO在半径为R的圆中,240o的圆心角所对的弧长 ,面积为2R2的扇形的圆心角等于 弧度。??课堂巩固例5. 已知扇形的周长为8 cm,面积为4 cm2,求该扇形的圆心角的弧度数.解:设扇形半径为r,弧长为l,则由?课堂实例?lrα? 如果一扇形的周长为20cm,问扇形的半径和圆心角各取什么值时,才能使扇形的面积最大??解:???????课堂巩固?课堂小结基本关系导出关系 ???????课后作业完成教材第10页A组6,7,8,9,10
B组2,3题祝各位同学:
身体健康 学习进步!
1.1.2《弧度制》第1课时 自我介绍 ?温故知新?2.弧长公式及扇形面积公式
提出问题1.度量角的方法“度分秒制”:把圆周角分为360等份—>1度的角—>60等份—>1分的角—>60等份—>1秒的角.?????????当n=600时呢??2.在同一个圆中,圆心角的大小与它所对的弧长一一对应.当半径不同时,同样大的圆心角所对的弧长不相等.
提出问题3、实验结果表明:当半径不同时,同样的圆心角所对的弧长与半径的比是常数.?称这个常数为该角的弧度数.能否用弧长来定义角的大小呢?我们把等于半径长的圆弧所对的圆心角叫做1弧度的角。单位符号是 rad,读作弧度弧度把角度单位与长度单位统一起来.弧度角的定义这种用弧度为单位来度量角的制度叫做弧度制思考:如果一个半径为r的圆的圆心角α所对的弧长是l,那么α的弧度数是多少? 如图:若圆的半径为2,圆心角∠AOB(正角)所对的圆弧长为4,那么 ∠AOB的弧度数就是24BoAα的正负由角α的终边旋转方向决定.?用“弧度”与“度”去度量每一个角时,除了零角以外,所得到的量数都是不同的,但它们既然是度量同一个角的结果,二者就可以相互换算. 若弧是一个整圆,它的圆心角是周角,其弧度数是2π,而在角度制里它是360°. 角度制与弧度制的换算 ∵ 360?=2? rad ,∴180?=? rad ??角度制与弧度制的换算写出一些特殊角的弧度数或角度 ??????????????课堂实例??课堂实例??1.把下列角的角度化为弧度?(1)36°=?????课堂练习12 °-1080 °?(2)210°=114°36'2.把下列角的弧度化为角度例3.用弧度制表示:
(1).终边在x轴上的角的集合
(2).终边在y轴上的角的集合
(3).终边在坐标轴上的角的集合
课堂实例????弧度制下的角与实数之间的关系是怎样的呢?弧度数用弧度来度量角,实际上角的集合与实数集R之间建立一 一对应的关系:正实数零负实数对应角的弧度数弧度数(1)都是度量角的大小的单位制
角度制的单位是“度”; (单位不能省略)
弧度制的单位是“弧度”; (单位可以省略)
?(4)两种单位制都与半径无关.角度制与弧度制(3)弧度制是十进制,它的表示是用一个实数表示,而角度制是六十进制; 1弧度≠1o课堂探究?弧长等于弧所对的圆心角(的弧度数)的绝对值与半径的积. 得到弧长公式:l=|α|·R??课堂探究表示的是在半径为R的圆中,弧长为l的弧所对的圆心角是αrad。l=|α|·R证明:设扇形所对的圆心角为no(αrad),则??课堂探究????课堂实例ABO在半径为R的圆中,240o的圆心角所对的弧长 ,面积为2R2的扇形的圆心角等于 弧度。??课堂巩固例5. 已知扇形的周长为8 cm,面积为4 cm2,求该扇形的圆心角的弧度数.解:设扇形半径为r,弧长为l,则由?课堂实例?lrα? 如果一扇形的周长为20cm,问扇形的半径和圆心角各取什么值时,才能使扇形的面积最大??解:???????课堂巩固?课堂小结基本关系导出关系 ???????课后作业完成教材第10页A组6,7,8,9,10
B组2,3题祝各位同学:
身体健康 学习进步!
