3.1.1-两角差的余弦公式(共23张PPT)
文档属性
| 名称 | 3.1.1-两角差的余弦公式(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-19 12:20:21 | ||
图片预览








文档简介
课件23张PPT。3.1.1 两角差的余弦公式1、熟悉用向量的数量积推导两角差的余弦公式的过程.
2、熟记并灵活运用两角差的余弦公式.
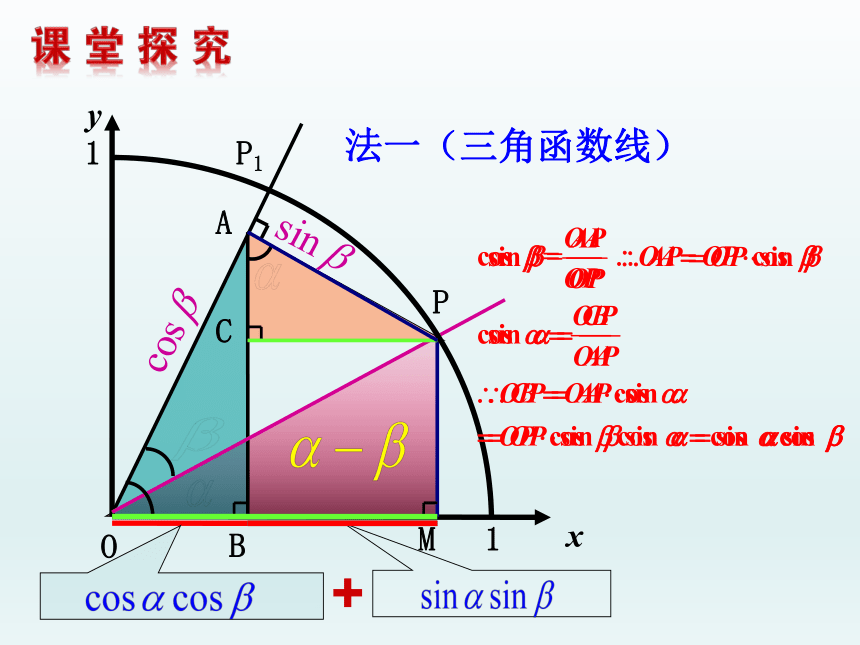
3、掌握“变角”和“拆角”的方法.自学教材P124—P127 解决下列问题一、熟记并灵活运用两角差的余弦公式. 二、《创新设计》 新知导学.三、《教材》 P127 练习1、2、3、4.xyPP1MBOAC+11法一(三角函数线)在单位圆中法二(向量法)两角差的余弦公式 两角和的余弦公式 口诀:余余正正符号反对于任意角α、β注意:1.公式的结构特点:同名相乘,符号相反3.当 时,公式变成一些诱导公式,因此一些诱导公式是 的特例.
当α,β中有一个角是90°的整数倍时,用诱导公式更便捷.2.公式要会正用、逆用、变形用完成本题后,你会求 的值吗?把非特殊角变为
特殊角,把未知角变为已知角. 利用同角的三角函数关系式求值时,要注意角的范围.三、《教材》 P127 练习1、2、3、4.提炼精华通过这节课的学习,你有什么收获?※对自己说,你有什么收获?
※对同学说,你有什么提示?
※对老师说,你有什么疑惑?1.两角和与差的余弦公式:2.已知一个角的正弦(或余弦)值,求该角的余弦(或正弦)值时, 要注意该角所在的象限,从而确定该角的三角函数值符号.3.在差角的余弦公式中, 既可以是单角,也可以是复角,运用时要注意角的变换,
如 , 等.
同时,公式的应用具有灵活性,解题时要注意正向、逆向和变式形式的选择.【预习】课本P128~P131《两角和与差的正弦、余弦、正切公式》必做题:《教材》 P137 A组1(1),(3)、2、3、4题 选做题:《教材》 P137 A组5题 2020年4月17日1次公式的逆用:解后回顾:角的整体性B原式=cos25 °cos35 °-sin25°sin35°
=cos(25°+35°) =cos60°解后回顾:用诱导公式变函数名称、变角 利用差角公式求值时,常常进行角的拆分与组合.即公式的变形应用.
2、熟记并灵活运用两角差的余弦公式.
3、掌握“变角”和“拆角”的方法.自学教材P124—P127 解决下列问题一、熟记并灵活运用两角差的余弦公式. 二、《创新设计》 新知导学.三、《教材》 P127 练习1、2、3、4.xyPP1MBOAC+11法一(三角函数线)在单位圆中法二(向量法)两角差的余弦公式 两角和的余弦公式 口诀:余余正正符号反对于任意角α、β注意:1.公式的结构特点:同名相乘,符号相反3.当 时,公式变成一些诱导公式,因此一些诱导公式是 的特例.
当α,β中有一个角是90°的整数倍时,用诱导公式更便捷.2.公式要会正用、逆用、变形用完成本题后,你会求 的值吗?把非特殊角变为
特殊角,把未知角变为已知角. 利用同角的三角函数关系式求值时,要注意角的范围.三、《教材》 P127 练习1、2、3、4.提炼精华通过这节课的学习,你有什么收获?※对自己说,你有什么收获?
※对同学说,你有什么提示?
※对老师说,你有什么疑惑?1.两角和与差的余弦公式:2.已知一个角的正弦(或余弦)值,求该角的余弦(或正弦)值时, 要注意该角所在的象限,从而确定该角的三角函数值符号.3.在差角的余弦公式中, 既可以是单角,也可以是复角,运用时要注意角的变换,
如 , 等.
同时,公式的应用具有灵活性,解题时要注意正向、逆向和变式形式的选择.【预习】课本P128~P131《两角和与差的正弦、余弦、正切公式》必做题:《教材》 P137 A组1(1),(3)、2、3、4题 选做题:《教材》 P137 A组5题 2020年4月17日1次公式的逆用:解后回顾:角的整体性B原式=cos25 °cos35 °-sin25°sin35°
=cos(25°+35°) =cos60°解后回顾:用诱导公式变函数名称、变角 利用差角公式求值时,常常进行角的拆分与组合.即公式的变形应用.
