人教版高中数学必修4 1.4.2正弦函数余弦函数的性质(共48张PPT)
文档属性
| 名称 | 人教版高中数学必修4 1.4.2正弦函数余弦函数的性质(共48张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-19 09:44:34 | ||
图片预览








文档简介
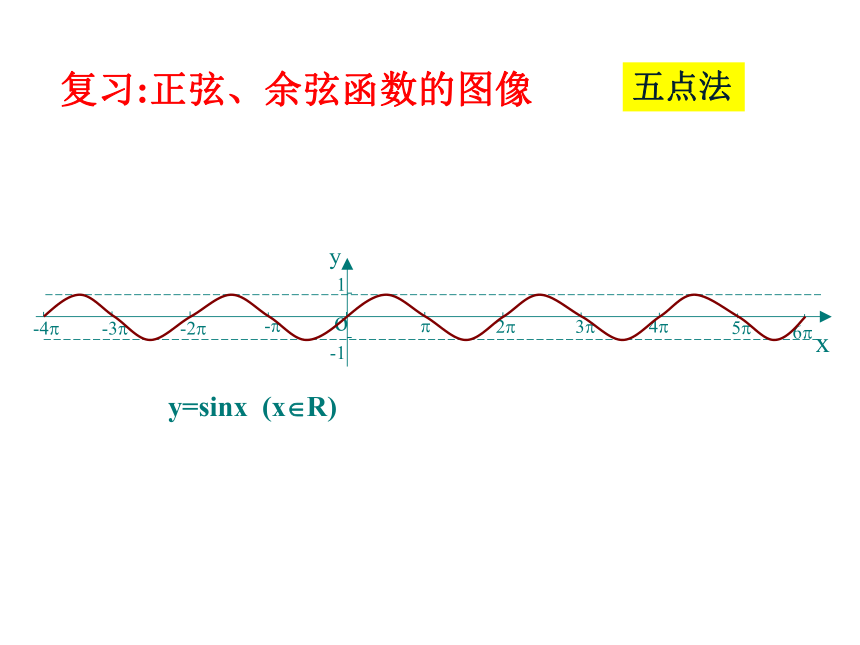
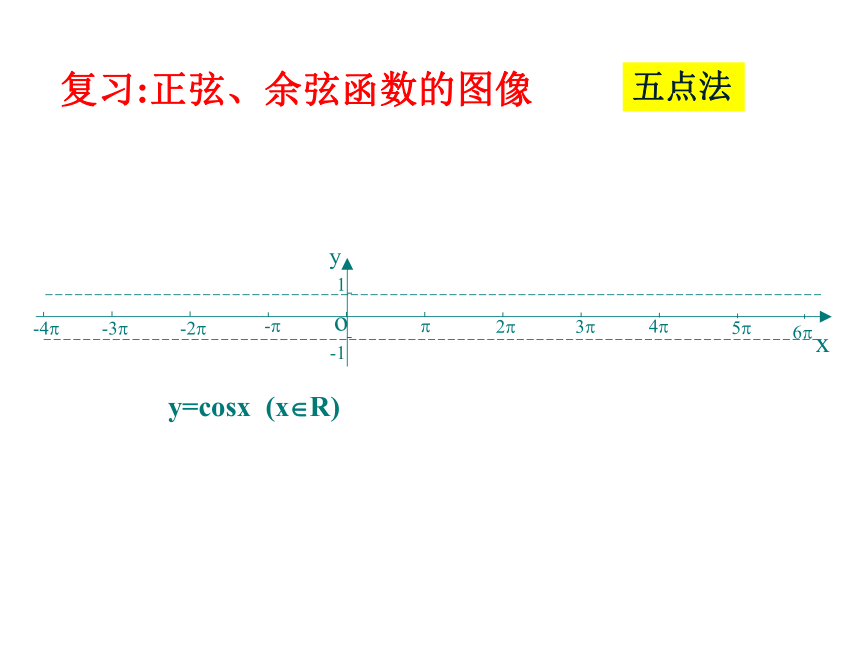
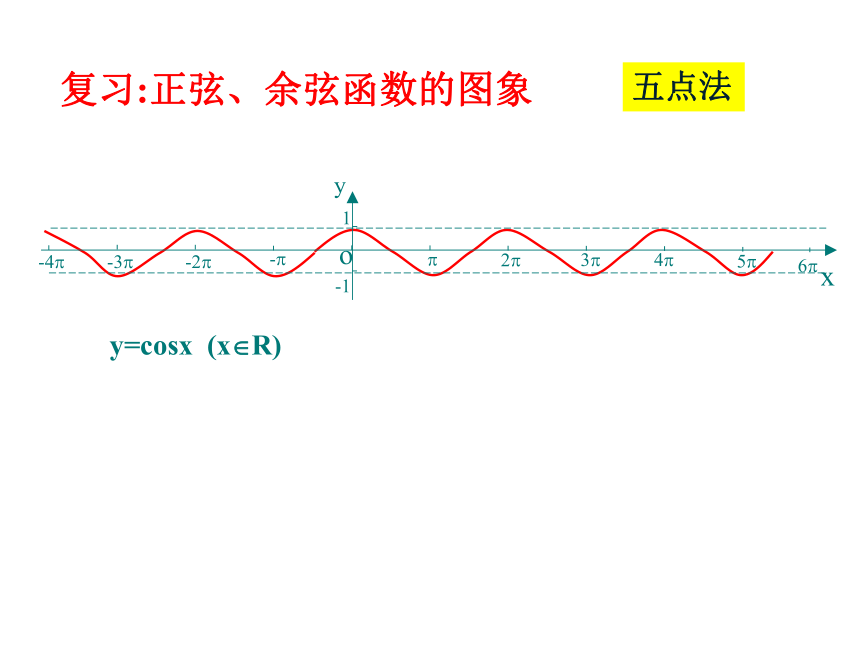
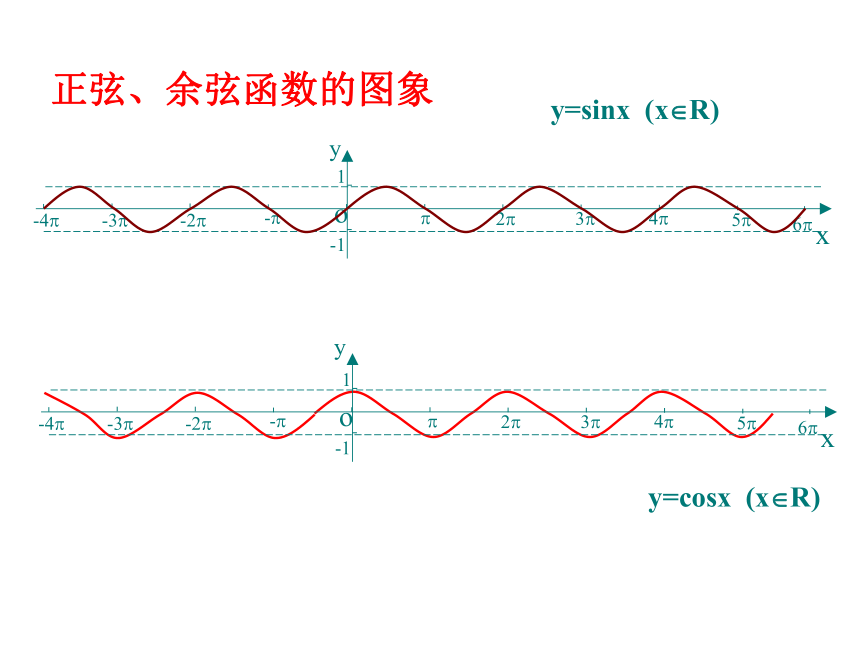
课件48张PPT。正弦函数、余弦函数的性质思考: 前面学习函数时,是如何研究它的性质?研究它的哪些性质?y=sinx (x?R) 复习:正弦、余弦函数的图像五点法y=sinx (x?R) 复习:正弦、余弦函数的图像五点法y=cosx (x?R) 复习:正弦、余弦函数的图像五点法 y=cosx (x?R) 复习:正弦、余弦函数的图象五点法y=sinx (x?R) y=cosx (x?R) 正弦、余弦函数的图象图像特点:周期循环周期(T)函数: 对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x)=f(x+T),那么函数f(x)就叫做周期函数.非零常数T叫做这个函数的周期.周期函数:图像语言:周期循环代数语言:思考2:正弦函数的周期有哪些?周期函数的周期是否惟一?思考1:等式sin(300+1200)=sin300是否成立?如果成立,能否说明1200是正弦函数y=sinx的一个周期吗?为什么?合作探究思考思考3: 正弦函数的最小正周期是多少?余弦函数呢?思考4:周期函数一定存在最小正周期吗?举例说明。 如果在周期函数f(x)的所有周期中存在一个最小的正数, 则这个最小正数叫做f(x)的最小正周期.最小正周期注:1.定义域中的每一个x,都有
2.若T是 的周期,则 也是其周期。
3.今后我们所涉及到的周期,若不特别说明,一般都是指函数的最小正周期。
4.周期函数不一定存在最小正周期。
5.周期函数性质的研究:
一个周期内 扩展到整个定义域例:求下列函数的周期:
(1)y=3cosx; (2)
(3)y=sin2x,;(4)y=2sin( ).思考:1.函数 的周期是多少?思考:1.函数 的周期是多少?函数 的周期是函数 的周期是课堂练习.求下列函数的周期:思考:2.若 的周期为T,则 的周期是多少? 呢?3. 的周期是多少? 呢?
呢?
例题:定义在R上的函数f(x)是周期为π是周期函数,且当x∈ 时,f(x)=sin x,求 的值.二.定义域和值域定义域:R值域:[-1,1]二.定义域和值域定义域:R值域:[-1,1]定义域:R值域:[-1,1]定义域:R值域:[-1,1]例题求使函数 取得最大值、最小值的
自变量的集合,并写出最大值、最小值。例题求使函数 取得最大值、最小值的
自变量的集合,并写出最大值、最小值。练习:求下列函数的值域练习:求下列函数的值域[0,2][-3,3][2,10]三.奇偶性奇函数三.奇偶性奇函数偶函数
探究:正弦函数的单调性四.单调性探究:正弦函数的单调性四.单调性单增区间为:单减区间为:探究:余弦函数的单调性探究:余弦函数的单调性单增区间为:单减区间为: 例3 比较下列各组数的大小:学以致用 利用诱导公式将角转化到同一单调区间内例:求 的单增区间。例:求 的单增区间。例:求 的单增区间。例:求 的单增区间。单调性的求法当 时,
增区间:减区间:当 时,化负为正五、正弦、余弦函数的对称性五、正弦、余弦函数的对称性y=sinx的图象对称轴为:y=sinx的图象对称中心为:y=cosx的图象对称轴为:y=cosx的图象对称中心为: 任意两相邻对称轴(或对称中心)的间距为半个周期;对称轴与其相邻的对称中心的间距为四分之一个周期.该函数的对称中心是______________。练习:函数 对任意的x都有 ,则 ( )A. 2或0 B.-2或2
C.0 D.-2或0 课堂小结:奇函数偶函数
2.若T是 的周期,则 也是其周期。
3.今后我们所涉及到的周期,若不特别说明,一般都是指函数的最小正周期。
4.周期函数不一定存在最小正周期。
5.周期函数性质的研究:
一个周期内 扩展到整个定义域例:求下列函数的周期:
(1)y=3cosx; (2)
(3)y=sin2x,;(4)y=2sin( ).思考:1.函数 的周期是多少?思考:1.函数 的周期是多少?函数 的周期是函数 的周期是课堂练习.求下列函数的周期:思考:2.若 的周期为T,则 的周期是多少? 呢?3. 的周期是多少? 呢?
呢?
例题:定义在R上的函数f(x)是周期为π是周期函数,且当x∈ 时,f(x)=sin x,求 的值.二.定义域和值域定义域:R值域:[-1,1]二.定义域和值域定义域:R值域:[-1,1]定义域:R值域:[-1,1]定义域:R值域:[-1,1]例题求使函数 取得最大值、最小值的
自变量的集合,并写出最大值、最小值。例题求使函数 取得最大值、最小值的
自变量的集合,并写出最大值、最小值。练习:求下列函数的值域练习:求下列函数的值域[0,2][-3,3][2,10]三.奇偶性奇函数三.奇偶性奇函数偶函数
探究:正弦函数的单调性四.单调性探究:正弦函数的单调性四.单调性单增区间为:单减区间为:探究:余弦函数的单调性探究:余弦函数的单调性单增区间为:单减区间为: 例3 比较下列各组数的大小:学以致用 利用诱导公式将角转化到同一单调区间内例:求 的单增区间。例:求 的单增区间。例:求 的单增区间。例:求 的单增区间。单调性的求法当 时,
增区间:减区间:当 时,化负为正五、正弦、余弦函数的对称性五、正弦、余弦函数的对称性y=sinx的图象对称轴为:y=sinx的图象对称中心为:y=cosx的图象对称轴为:y=cosx的图象对称中心为: 任意两相邻对称轴(或对称中心)的间距为半个周期;对称轴与其相邻的对称中心的间距为四分之一个周期.该函数的对称中心是______________。练习:函数 对任意的x都有 ,则 ( )A. 2或0 B.-2或2
C.0 D.-2或0 课堂小结:奇函数偶函数
