人教版高中数学必修4 2.3平面向量基本定理正交分解及其坐标表示(共176张PPT)
文档属性
| 名称 | 人教版高中数学必修4 2.3平面向量基本定理正交分解及其坐标表示(共176张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-19 00:00:00 | ||
图片预览





文档简介
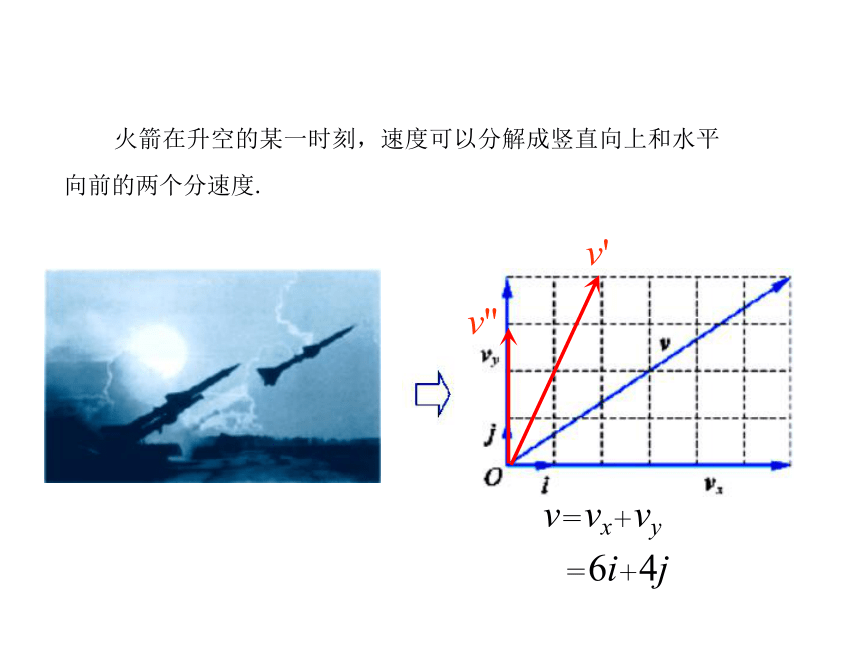
课件175张PPT。2.3平
面向
量的基本定
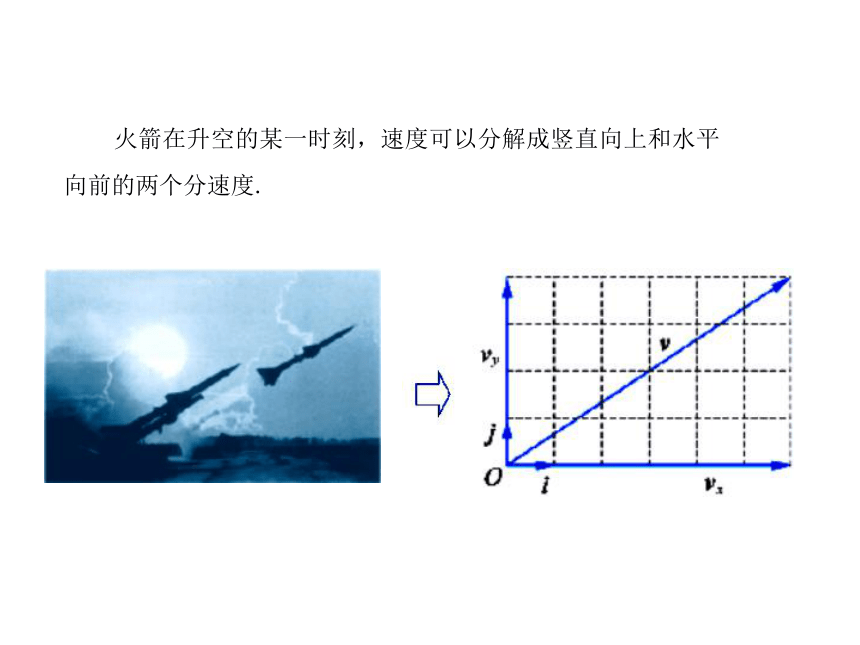
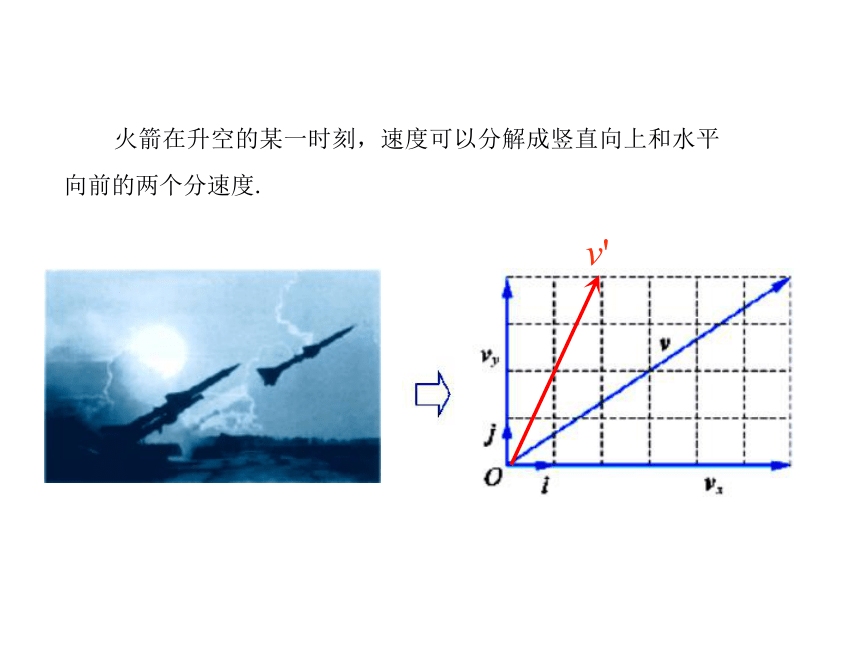
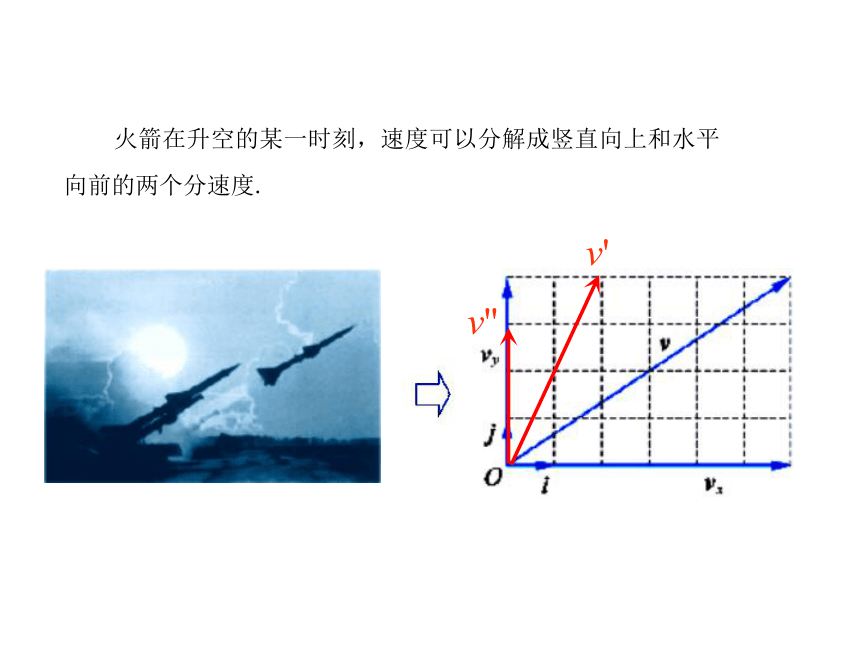
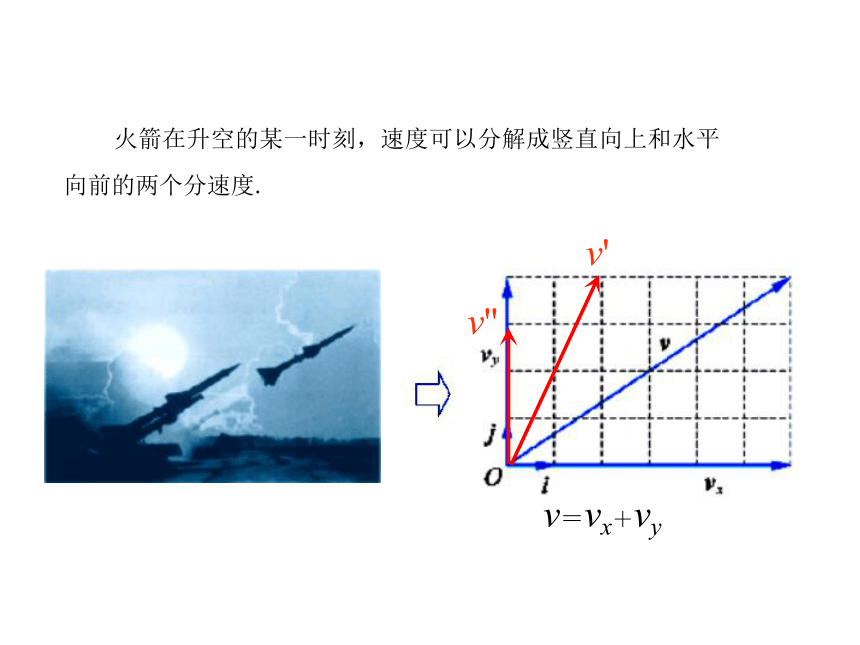
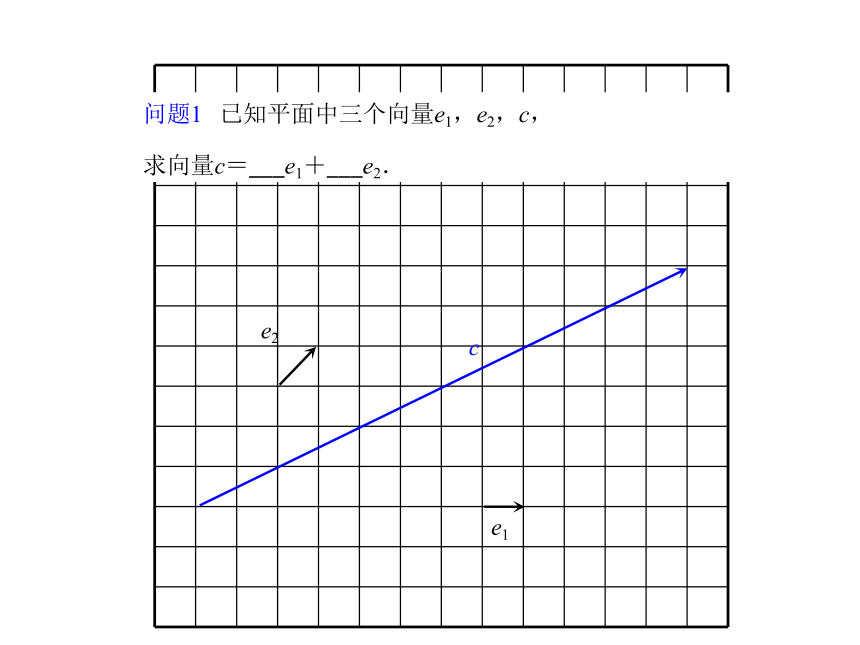
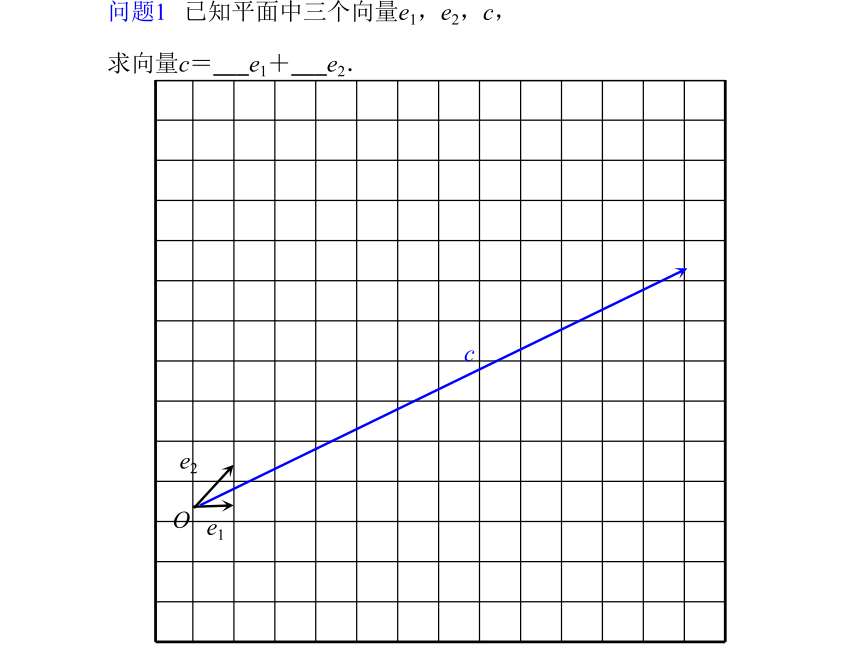
理及坐标表示高中数学 必修4 2.3.1 平面向量基本定理 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度. 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度. 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度.v' 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度.v'v'' 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度.v'v''v=vx+vy 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度.v'v''v=vx+vy=6i+4je1e2c问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cO问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cO问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cOC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cOC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cOC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cONC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cOMNC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cOMNC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.66e1e2cOMNC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.66 向量d=___e1+___e2e1e2 向量d=___e1+___e2e1e2 向量d=___e1+___e2OMNe1e2D 向量d=___e1+___e2OMN24e1e2D 向量f=___e1+___e2e2e1 向量f=___e1+___e2e2e1F 向量f=___e1+___e2e2e1F 向量f=___e1+___e2e2e1F-e1OMNf 向量f=___e1+___e2e2F-e1OMNf 向量f=___e1+___e2(-4)3e2FOe1e2Oe1e2Oe1e2问题2 如果e1,e2是平面内任意两向量,那么平面内的任一向量a还可以表示成a=?1e1+?2e2的形式吗?e2a
如果e1,e2是同一平面内两个不共线的向量,那么对于这一平面内
的任一向量a,有且只有一对实数?1,?2,使a=?1e1+?2e2.平面向量基本定理:
如果e1,e2是同一平面内两个不共线的向量,那么对于这一平面内
的任一向量a,有且只有一对实数?1,?2,使a=?1e1+?2e2.平面向量基本定理:
如果e1,e2是同一平面内两个不共线的向量,那么对于这一平面内
的任一向量a,有且只有一对实数?1,?2,使a=?1e1+?2e2.(1)我们把不共线的向量e1,e2叫做表示这一平面内所有向量的一组
基底(base) ;平面向量基本定理:
如果e1,e2是同一平面内两个不共线的向量,那么对于这一平面内
的任一向量a,有且只有一对实数?1,?2,使a=?1e1+?2e2.(1)我们把不共线的向量e1,e2叫做表示这一平面内所有向量的一组
基底(base) ;(2)一个平面向量用一组基底e1,e2表示成 a=?1e1+?2e2的形式,我
们称它为向量的分解. 若e1,e2是平面内向量的一组基底,则下面的向量中不能作为一组基底的是
A. e1+e2和e1-e2 B. 3e1-2 e2和-6e1+4 e2
C. e1+3 e2和3 e1+e2 D. e1+e2和 e2 ( )练习: 若e1,e2是平面内向量的一组基底,则下面的向量中不能作为一组基底的是
A. e1+e2和e1-e2 B. 3e1-2 e2和-6e1+4 e2
C. e1+3 e2和3 e1+e2 D. e1+e2和 e2 ( )练习:B例1 如图所示,平行四边形ABCD的两条对角线相交于点M,且
AB=a,AD=b,用a,b表示MA,MB,MC,MD.ABDM 如图所示,?ABD中,M是边BD的中点,且AB=a,AD=b,
用a,b表示AM,MB.变式:ABDM 如图所示,?ABD中,M是边BD的中点,且AB=a,AD=b,
用a,b表示AM,MB.变式:EF向量的夹角与垂直
向量都有方向,两个向量正向的夹角就是平面向量的夹角,如∠AOB=60°,就是指向量OA与OB夹角为60°,而说向量AO与向量OB夹角,那就是120°了。 向量夹角的范围是[0°,180°] 平面向量基本定理,其实质在于:同一平面内任一向量都可以表示为两个不共线向量e1,e2的线性组合,且e1,e2是这一平面内所有向量的一组基底. 小结: 思考: 已知向量e1,e2不共线,若向量λ e1-e2 与向量e1 -λ e2共线,求实数λ的值.? 析:∵λ e1 - e2与e1 -λ e2共线? ∴存在实数k,使λ e1 - e2 =k( e1 -λ e2 ), 化简得(λ-k) e1 +(kλ-1) e2 =0? ∵ e1 、 e2不共线?, ∴由平面向量的基本定理可知: λ-k=0且kλ-1=0? 解得λ=±1,故λ=±1.高中数学 必修4 2.3.2平面向量的正交分解及坐标表示
2.3.3平面向量的坐标运算
平面向量的正交分解平面向量的正交分解平面向量的正交分解平面向量的正交分解平面向量的坐标表示平面向量的坐标表示平面向量的坐标表示平面向量的坐标表示(1,0)
(0,1)
(0,0)平面向量的坐标表示(1,0)
(0,1)
(0,0)平面向量的坐标表示①①OxyOxyOxyOxyOxyOxyAOxyAOxyA2.点A的坐标与向量 的坐标的关系?2.点A的坐标与向量 的坐标的关系?两者相同2.点A的坐标与向量 的坐标的关系?两者相同2.点A的坐标与向量 的坐标的关系?两者相同AA1A2AA1A2解:如图可知AA1A2解:如图可知AA1A2解:如图可知AA1A2解:如图可知同理AA1A2解:如图可知同理问题:若已知 =(1 ,3) , =(5 ,1), 问题:若已知 =(1 ,3) , =(5 ,1), 问题:若已知 =(1 ,3) , =(5 ,1), 问题:若已知 =(1 ,3) , =(5 ,1), 问题:若已知 =(1 ,3) , =(5 ,1), 问题:若已知 =(1 ,3) , =(5 ,1), (6,4)问题:若已知 =(1 ,3) , =(5 ,1), (6,4)问题:若已知 =(1 ,3) , =(5 ,1), (6,4)问题:若已知 =(1 ,3) , =(5 ,1), (6,4)问题:若已知 =(1 ,3) , =(5 ,1), (6,4)问题:若已知 =(1 ,3) , =(5 ,1), (6,4)猜想:问题:若已知 =(1 ,3) , =(5 ,1), (6,4)猜想:问题:若已知 =(1 ,3) , =(5 ,1), (6,4)猜想:问题:若已知 =(1 ,3) , =(5 ,1), (6,4)猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) 问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) 问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) 问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) 平面向量的坐标运算法则平面向量的坐标运算法则平面向量的坐标运算法则平面向量的坐标运算法则平面向量的坐标运算法则结论:两个向量和(差)的坐标分别等于这两个向量
相应坐标的和(差)。 向量的数乘运算 向量的数乘运算 向量的数乘运算 向量的数乘运算? 向量的数乘运算? 向量的数乘运算 向量的数乘运算 向量的数乘运算 向量的数乘运算 向量的数乘运算 向量的数乘运算结论:实数与向量的积的坐标等于这个实数乘原来向量的相应坐标平面向量的坐标运算法则例例(-1,5)例(-1,5)(5,-3)例(-1,5)(5,-3)(-6,19) 例2
已知A、B两点的坐标,求 ,
的坐标。
⑴ A (3,5) , B (6,9) ; ⑵ A(-3,4) , B(6,3)
⑶ A (0,3) , B (0,5) ; ⑷ A (3,0), B(8,0) 例2
已知A、B两点的坐标,求 ,
的坐标。
⑴ A (3,5) , B (6,9) ; ⑵ A(-3,4) , B(6,3)
⑶ A (0,3) , B (0,5) ; ⑷ A (3,0), B(8,0)终点B始点A 终点B始点A ( 2,3 )终点B始点A ( 2,3 )( 1,1 )终点B始点A ( -2 , 7 ) ( 2,3 )( 1,1 )终点B始点A ( -2 , 7 ) ( 3 , -4 ) ( 2,3 )( 1,1 )终点B始点A ( -2 , 7 ) ( 3 , -4 ) ( 1,2 )( 2,3 )( 1,1 )终点B始点A ( -2 , 7 ) ( 3 , -4 ) ( 1,3 )( 1,2 )( 2,3 )( 1,1 )终点B始点A ( -2 , 7 )终点坐标减去向量坐标 ( 3 , -4 ) ( 1,3 )( 1,2 )( 2,3 )( 1,1 )终点B始点A ( -2 , 7 )终点坐标减去向量坐标始点坐标加上向量坐标 ( 3 , -4 ) ( 1,3 )( 1,2 )( 2,3 )( 1,1 )终点B始点A终点坐标减去始点坐标 ( -2 , 7 )终点坐标减去向量坐标始点坐标加上向量坐标 ( 3 , -4 ) ( 1,3 )( 1,2 )( 2,3 )( 1,1 )例3.如图,已知 四边形 的四个顶点A、B、C,D的坐标分别是(-2,1)、(-1,3)、(3,4),(2,2)求证四边形 ABCD是平行四边形 xy-1-1-2-5-66例3.如图,已知 四边形 的四个顶点A、B、C,D的坐标分别是(-2,1)、(-1,3)、(3,4),(2,2)求证四边形 ABCD是平行四边形 xy-1-1-2-5-66解:设点D的坐标为(x,y)解:设点D的坐标为(x,y)解:设点D的坐标为(x,y)解:设点D的坐标为(x,y)解:设点D的坐标为(x,y)解得 x=2,y=2解:设点D的坐标为(x,y)解得 x=2,y=2所以顶点D的坐标为(2,2)另解:由平行四边形法则可得另解:由平行四边形法则可得另解:由平行四边形法则可得而另解:由平行四边形法则可得而所以顶点D的坐标为(2,2)思考2:若已知平面上三个点A、B、C 的坐标分别为(-2,1),(-1,3),(3,4),求第四个点的坐标,使这四个点构成一个平行四边形的四个顶点.xy-1-1-2-5-66Dxy-1-1-2-5-66Dxy-1-1-2-5-66D请回顾本堂课的教学过程,你能说说你学了哪些知识吗?1.平面向量坐标的加.减运算法则 =( x1 , y1) + (x2 ,? y2)= (x1+x2 , y1+y2)=( x1 , y1) - (x2 ,? y2)= (x1- x2 , y1-y2)2.平面向量坐标实数与向量相乘的运算法则3.平面向量坐标若A(x1 , y1) , B(x2 , y2) =( x1 , y1) + (x2 ,? y2)= (x1+x2 , y1+y2)
面向
量的基本定
理及坐标表示高中数学 必修4 2.3.1 平面向量基本定理 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度. 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度. 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度.v' 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度.v'v'' 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度.v'v''v=vx+vy 火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度.v'v''v=vx+vy=6i+4je1e2c问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cO问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cO问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cOC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cOC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cOC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cONC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cOMNC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.e1e2cOMNC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.66e1e2cOMNC问题1 已知平面中三个向量e1,e2,c,
求向量c=___e1+___e2.66 向量d=___e1+___e2e1e2 向量d=___e1+___e2e1e2 向量d=___e1+___e2OMNe1e2D 向量d=___e1+___e2OMN24e1e2D 向量f=___e1+___e2e2e1 向量f=___e1+___e2e2e1F 向量f=___e1+___e2e2e1F 向量f=___e1+___e2e2e1F-e1OMNf 向量f=___e1+___e2e2F-e1OMNf 向量f=___e1+___e2(-4)3e2FOe1e2Oe1e2Oe1e2问题2 如果e1,e2是平面内任意两向量,那么平面内的任一向量a还可以表示成a=?1e1+?2e2的形式吗?e2a
如果e1,e2是同一平面内两个不共线的向量,那么对于这一平面内
的任一向量a,有且只有一对实数?1,?2,使a=?1e1+?2e2.平面向量基本定理:
如果e1,e2是同一平面内两个不共线的向量,那么对于这一平面内
的任一向量a,有且只有一对实数?1,?2,使a=?1e1+?2e2.平面向量基本定理:
如果e1,e2是同一平面内两个不共线的向量,那么对于这一平面内
的任一向量a,有且只有一对实数?1,?2,使a=?1e1+?2e2.(1)我们把不共线的向量e1,e2叫做表示这一平面内所有向量的一组
基底(base) ;平面向量基本定理:
如果e1,e2是同一平面内两个不共线的向量,那么对于这一平面内
的任一向量a,有且只有一对实数?1,?2,使a=?1e1+?2e2.(1)我们把不共线的向量e1,e2叫做表示这一平面内所有向量的一组
基底(base) ;(2)一个平面向量用一组基底e1,e2表示成 a=?1e1+?2e2的形式,我
们称它为向量的分解. 若e1,e2是平面内向量的一组基底,则下面的向量中不能作为一组基底的是
A. e1+e2和e1-e2 B. 3e1-2 e2和-6e1+4 e2
C. e1+3 e2和3 e1+e2 D. e1+e2和 e2 ( )练习: 若e1,e2是平面内向量的一组基底,则下面的向量中不能作为一组基底的是
A. e1+e2和e1-e2 B. 3e1-2 e2和-6e1+4 e2
C. e1+3 e2和3 e1+e2 D. e1+e2和 e2 ( )练习:B例1 如图所示,平行四边形ABCD的两条对角线相交于点M,且
AB=a,AD=b,用a,b表示MA,MB,MC,MD.ABDM 如图所示,?ABD中,M是边BD的中点,且AB=a,AD=b,
用a,b表示AM,MB.变式:ABDM 如图所示,?ABD中,M是边BD的中点,且AB=a,AD=b,
用a,b表示AM,MB.变式:EF向量的夹角与垂直
向量都有方向,两个向量正向的夹角就是平面向量的夹角,如∠AOB=60°,就是指向量OA与OB夹角为60°,而说向量AO与向量OB夹角,那就是120°了。 向量夹角的范围是[0°,180°] 平面向量基本定理,其实质在于:同一平面内任一向量都可以表示为两个不共线向量e1,e2的线性组合,且e1,e2是这一平面内所有向量的一组基底. 小结: 思考: 已知向量e1,e2不共线,若向量λ e1-e2 与向量e1 -λ e2共线,求实数λ的值.? 析:∵λ e1 - e2与e1 -λ e2共线? ∴存在实数k,使λ e1 - e2 =k( e1 -λ e2 ), 化简得(λ-k) e1 +(kλ-1) e2 =0? ∵ e1 、 e2不共线?, ∴由平面向量的基本定理可知: λ-k=0且kλ-1=0? 解得λ=±1,故λ=±1.高中数学 必修4 2.3.2平面向量的正交分解及坐标表示
2.3.3平面向量的坐标运算
平面向量的正交分解平面向量的正交分解平面向量的正交分解平面向量的正交分解平面向量的坐标表示平面向量的坐标表示平面向量的坐标表示平面向量的坐标表示(1,0)
(0,1)
(0,0)平面向量的坐标表示(1,0)
(0,1)
(0,0)平面向量的坐标表示①①OxyOxyOxyOxyOxyOxyAOxyAOxyA2.点A的坐标与向量 的坐标的关系?2.点A的坐标与向量 的坐标的关系?两者相同2.点A的坐标与向量 的坐标的关系?两者相同2.点A的坐标与向量 的坐标的关系?两者相同AA1A2AA1A2解:如图可知AA1A2解:如图可知AA1A2解:如图可知AA1A2解:如图可知同理AA1A2解:如图可知同理问题:若已知 =(1 ,3) , =(5 ,1), 问题:若已知 =(1 ,3) , =(5 ,1), 问题:若已知 =(1 ,3) , =(5 ,1), 问题:若已知 =(1 ,3) , =(5 ,1), 问题:若已知 =(1 ,3) , =(5 ,1), 问题:若已知 =(1 ,3) , =(5 ,1), (6,4)问题:若已知 =(1 ,3) , =(5 ,1), (6,4)问题:若已知 =(1 ,3) , =(5 ,1), (6,4)问题:若已知 =(1 ,3) , =(5 ,1), (6,4)问题:若已知 =(1 ,3) , =(5 ,1), (6,4)问题:若已知 =(1 ,3) , =(5 ,1), (6,4)猜想:问题:若已知 =(1 ,3) , =(5 ,1), (6,4)猜想:问题:若已知 =(1 ,3) , =(5 ,1), (6,4)猜想:问题:若已知 =(1 ,3) , =(5 ,1), (6,4)猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:问题:若已知 =(1 ,3) , =(5 ,1), 猜想:?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) ?问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) 问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) 问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) 问题:若已知 =(1 ,3) , =(5 ,1), 猜想:=(x1 , ) + ( , y2 ) 平面向量的坐标运算法则平面向量的坐标运算法则平面向量的坐标运算法则平面向量的坐标运算法则平面向量的坐标运算法则结论:两个向量和(差)的坐标分别等于这两个向量
相应坐标的和(差)。 向量的数乘运算 向量的数乘运算 向量的数乘运算 向量的数乘运算? 向量的数乘运算? 向量的数乘运算 向量的数乘运算 向量的数乘运算 向量的数乘运算 向量的数乘运算 向量的数乘运算结论:实数与向量的积的坐标等于这个实数乘原来向量的相应坐标平面向量的坐标运算法则例例(-1,5)例(-1,5)(5,-3)例(-1,5)(5,-3)(-6,19) 例2
已知A、B两点的坐标,求 ,
的坐标。
⑴ A (3,5) , B (6,9) ; ⑵ A(-3,4) , B(6,3)
⑶ A (0,3) , B (0,5) ; ⑷ A (3,0), B(8,0) 例2
已知A、B两点的坐标,求 ,
的坐标。
⑴ A (3,5) , B (6,9) ; ⑵ A(-3,4) , B(6,3)
⑶ A (0,3) , B (0,5) ; ⑷ A (3,0), B(8,0)终点B始点A 终点B始点A ( 2,3 )终点B始点A ( 2,3 )( 1,1 )终点B始点A ( -2 , 7 ) ( 2,3 )( 1,1 )终点B始点A ( -2 , 7 ) ( 3 , -4 ) ( 2,3 )( 1,1 )终点B始点A ( -2 , 7 ) ( 3 , -4 ) ( 1,2 )( 2,3 )( 1,1 )终点B始点A ( -2 , 7 ) ( 3 , -4 ) ( 1,3 )( 1,2 )( 2,3 )( 1,1 )终点B始点A ( -2 , 7 )终点坐标减去向量坐标 ( 3 , -4 ) ( 1,3 )( 1,2 )( 2,3 )( 1,1 )终点B始点A ( -2 , 7 )终点坐标减去向量坐标始点坐标加上向量坐标 ( 3 , -4 ) ( 1,3 )( 1,2 )( 2,3 )( 1,1 )终点B始点A终点坐标减去始点坐标 ( -2 , 7 )终点坐标减去向量坐标始点坐标加上向量坐标 ( 3 , -4 ) ( 1,3 )( 1,2 )( 2,3 )( 1,1 )例3.如图,已知 四边形 的四个顶点A、B、C,D的坐标分别是(-2,1)、(-1,3)、(3,4),(2,2)求证四边形 ABCD是平行四边形 xy-1-1-2-5-66例3.如图,已知 四边形 的四个顶点A、B、C,D的坐标分别是(-2,1)、(-1,3)、(3,4),(2,2)求证四边形 ABCD是平行四边形 xy-1-1-2-5-66解:设点D的坐标为(x,y)解:设点D的坐标为(x,y)解:设点D的坐标为(x,y)解:设点D的坐标为(x,y)解:设点D的坐标为(x,y)解得 x=2,y=2解:设点D的坐标为(x,y)解得 x=2,y=2所以顶点D的坐标为(2,2)另解:由平行四边形法则可得另解:由平行四边形法则可得另解:由平行四边形法则可得而另解:由平行四边形法则可得而所以顶点D的坐标为(2,2)思考2:若已知平面上三个点A、B、C 的坐标分别为(-2,1),(-1,3),(3,4),求第四个点的坐标,使这四个点构成一个平行四边形的四个顶点.xy-1-1-2-5-66Dxy-1-1-2-5-66Dxy-1-1-2-5-66D请回顾本堂课的教学过程,你能说说你学了哪些知识吗?1.平面向量坐标的加.减运算法则 =( x1 , y1) + (x2 ,? y2)= (x1+x2 , y1+y2)=( x1 , y1) - (x2 ,? y2)= (x1- x2 , y1-y2)2.平面向量坐标实数与向量相乘的运算法则3.平面向量坐标若A(x1 , y1) , B(x2 , y2) =( x1 , y1) + (x2 ,? y2)= (x1+x2 , y1+y2)
