沪科版七上数学第3章3.2方案问题与计费问题 教学课件(29张PPT)
文档属性
| 名称 | 沪科版七上数学第3章3.2方案问题与计费问题 教学课件(29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 606.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 15:31:45 | ||
图片预览






文档简介
(共29张PPT)
第3章 一次方程与方程组
3.2 一元一次方程的应用
方案问题和计费问题
1
课堂讲解
方案优化问题
分段计费问题
2
课时流程
逐点
导讲练
课堂小结
课后作业
1
知识点
方案优化问题
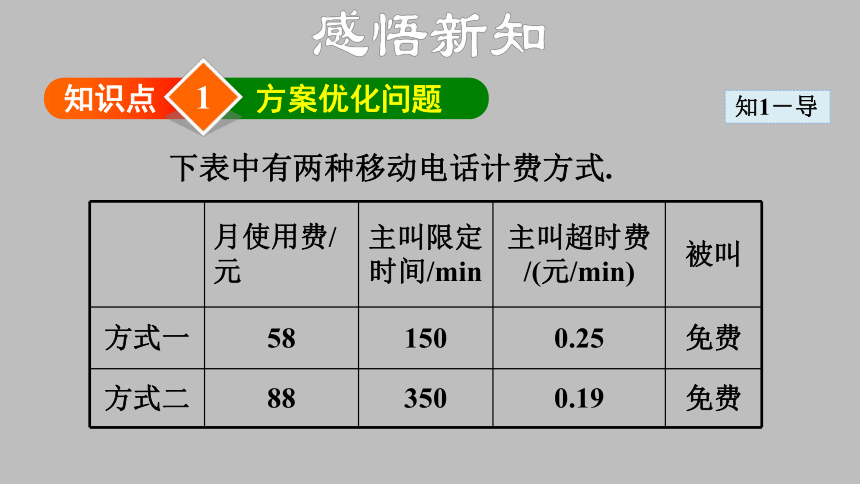
下表中有两种移动电话计费方式.
月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
考虑下列问题:
(1)设一个月内用移动电话主叫为tmin (t 是正整数).根据上表,列表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费固定收;主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
分析: (1)由上表可知,计费与主叫时间相关,计费时首先要看主 叫是否 超过限定时间.因此,考虑t的取值时,两个主叫限定时间150 min和350 min 是不同时间范围的划分点.当t在不同时间范围内取值时,方式一和方式二的计费如下页表:
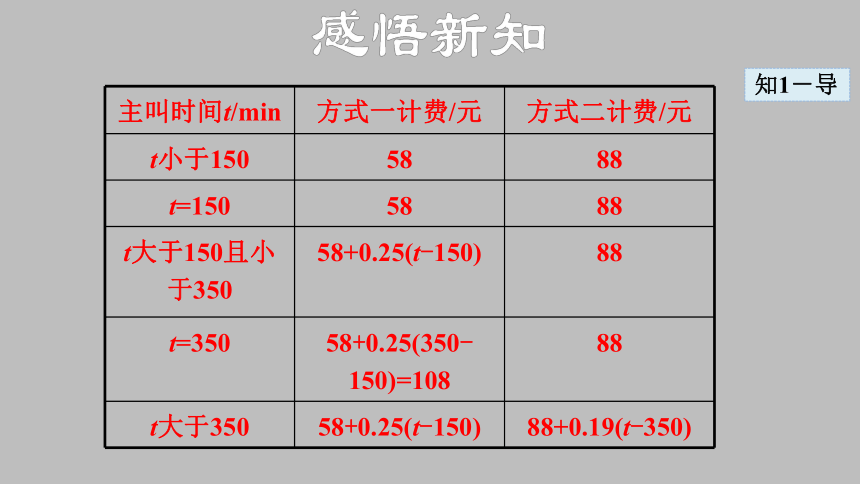
主叫时间t/min 方式一计费/元 方式二计费/元
t小于150 58 88
t=150 58 88
t大于150且小于350 58+0.25(t-150)
88
t=350 58+0.25(350-150)=108 88
t大于350 58+0.25(t-150) 88+0.19(t-350)
(2)观察(1)中的表,可以发现:主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的计费少也会变化.下面比较不同时间范围内方式一和方式二的计费情况.
①当t小于或等于150时,按方式一的计费少.
②当t从150增加到350时,按方式一的计费由58元增加到108元,而按方式二的计费一直是88元.因此,当t大于150并且小于350时,可能在某主叫时间按方式一和方式二的计费相等.列方程58+0.25(t—150) = 88,解得t=270.
因此,如果主叫时间恰是270 min,按两种方式的计费相等,都是88元; 如果主叫时间大于150 min且小于270 min,按方式一的计费少于按方式二的计费(88元);如果主叫时间大于270 min且小于350 min,按方式一的计费多于按方式二的计费(88元).
③当t=350时,按方式二的计费少.
④当t大于350时,可以看出,按方式一的 计费为108元加上超过350 min部分的超时费 (0.25(t-350)),按方式二的计费为88元加上超 过350 min部分的超时费(0.19(t-350)),按方式二的计费少.
综合以上的分析,可以发现:
___________时,选择方案一省钱;
___________时,选择方案二省钱.
选一些具体数字,通过计算验证你的发现是否正确.
当t大于350 时,按方式一
的计费 58+0.25(t-150)
可变 形为 108 + 0.25(t - 350).对比按方式二 的计费,你能说明此 时按哪种方式的计费少吗?
t<270
t>270
解答这类问题的一般步骤:
1.运用一元一次方程解应用题的方法,求解使方案值相等的情况;
2.用特殊值试探去选择方案,取小于(或大于)一元一次方程解 的值,比较两种方案的优劣后下结论.
例1 某市上网有两种收费方案,用户可任选其一:A为计时制——1元/时;B为包月制——80元/月,此外每种上网方式都附加通讯费0.1元/时.
(1)某用户每月上网40小时,选哪种方式比较合算?
(2)某用户每月有110元钱用于上网,选哪种方式比较合算?
(3)请你设计一个方案,使用户能合理地选择上网方式.
导引:(1)提供了上网时间40小时,根据“单价×总时长=总价”,求出A,B收费方案下的费用,进行比较;(2)提供了上网的总费用,已知上网的单价,求出总时长进行比较;(3)根据用户的上网时长,比较哪种方案收费较少,帮其设计合理的方案.
解:(1)如果用户每月上网40小时:
A计时制:40×(0.1+1)=44(元),
B包月制:80+40×0.1=84(元),
44<84,故选A计时制比较合算.
(2)设用户用110元上网,A计时制可上网x小时,
B包月制可上网y小时,
则(1+0.1)x=110,解得x=100,
80+0.1 y=110,解得y =300.
因为100<300,故选B包月制比较合算.
(3)设用户上网z小时,两种方式收费一样多.
则(1+0.1)z=80+0.1z.
解得z=80.
故上网不足80小时,选A计时制;
上网超过80小时,选B包月制;
上网恰好80小时,两种方案都一样.
B
1
张老师一家三口暑假准备参加旅游团去北京旅游,甲旅行社说:“如果父母买全票,小孩可半价优惠”;乙旅行社说:“全部按全票价的8折优惠”,若全票价为1 200元.则张老师应选择哪家旅行社?( )
A.选择甲 B.选择乙
C.选择甲、乙都一样 D.无法确定
2
某校准备为毕业班学生制作一批纪念册.甲公司提出:每册收材料费5元,另收设计费1 500元;乙公司提出:每册收材料费8元,不收设计费.张老师经过计算,发现两家公司收费一样,则该校今年毕业生有_______人.
500
2
知识点
分段计费问题
例2 近几年我国部分地区不时出现的严重干旱,使我们认识 到节水的重要性.为了加强公民的节水意识,合理利用水资源,某市对自来水收费采用阶梯价格的调控手段以达到节水的目的.
该市自来水收费价格见价目表.
价目表
每月用水量 单价
不超出6 m3的部分 2元/m3
超出6 m3但不超出10 m3的部分 4元/m3
超出10 m3的部分 8元/m3
注:水费按月结算
(1)若某户居民2月份用水10.5 m3,应交水费多少元?
(2)若该户居民3,4月份共用水16 m3(4月份用水量超过3月份),共交水费44元,则该户居民3,4月份各用水多少立方米?(结果精确到0.1 m3)
解:(1)由题意,得2×6+4×(10-6)+8×(10.5-10)=32(元).
所以二月份应交水费32元.
(2)设三月份用水x m3,则四月份用水(16-x) m3.
①当x≤6时,16-x≥10,
依题意,得2x+2×6+4×4+8(16-x-10)=44.
整理,得6x=32,所以x≈5.3,此时16-x≈10.7,符合题意.
②当6<x≤10时,6≤16-x<10,依题意,
得2×6+4×(x-6)+2×6+4(16-x-6)=44.
整理,得40=44,此方程无解.所以6<x≤10不可能成立.
③因为4月份用水量超过3月份,所以x不可能超过10.
综上所述,三月份用水约5.3 m3,四月份用水约10.7 m3.
1
参加保险公司的医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表:
住院医疗费 报销率(%)
不超过500元的部分 0
超过500~1 000元的部分 60
超过1 000~3 000元的部分 80
… …
D
某人住院治疗后得到保险公司报销金额是1 100元,那么此人住院的医疗费是( )
A.1 000元 B.1 250元
C.1 500元 D.2 000元
谈谈本节课学到了哪些知识?学后有何感受?
请完成对应习题
第3章 一次方程与方程组
3.2 一元一次方程的应用
方案问题和计费问题
1
课堂讲解
方案优化问题
分段计费问题
2
课时流程
逐点
导讲练
课堂小结
课后作业
1
知识点
方案优化问题
下表中有两种移动电话计费方式.
月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
考虑下列问题:
(1)设一个月内用移动电话主叫为tmin (t 是正整数).根据上表,列表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费固定收;主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
分析: (1)由上表可知,计费与主叫时间相关,计费时首先要看主 叫是否 超过限定时间.因此,考虑t的取值时,两个主叫限定时间150 min和350 min 是不同时间范围的划分点.当t在不同时间范围内取值时,方式一和方式二的计费如下页表:
主叫时间t/min 方式一计费/元 方式二计费/元
t小于150 58 88
t=150 58 88
t大于150且小于350 58+0.25(t-150)
88
t=350 58+0.25(350-150)=108 88
t大于350 58+0.25(t-150) 88+0.19(t-350)
(2)观察(1)中的表,可以发现:主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的计费少也会变化.下面比较不同时间范围内方式一和方式二的计费情况.
①当t小于或等于150时,按方式一的计费少.
②当t从150增加到350时,按方式一的计费由58元增加到108元,而按方式二的计费一直是88元.因此,当t大于150并且小于350时,可能在某主叫时间按方式一和方式二的计费相等.列方程58+0.25(t—150) = 88,解得t=270.
因此,如果主叫时间恰是270 min,按两种方式的计费相等,都是88元; 如果主叫时间大于150 min且小于270 min,按方式一的计费少于按方式二的计费(88元);如果主叫时间大于270 min且小于350 min,按方式一的计费多于按方式二的计费(88元).
③当t=350时,按方式二的计费少.
④当t大于350时,可以看出,按方式一的 计费为108元加上超过350 min部分的超时费 (0.25(t-350)),按方式二的计费为88元加上超 过350 min部分的超时费(0.19(t-350)),按方式二的计费少.
综合以上的分析,可以发现:
___________时,选择方案一省钱;
___________时,选择方案二省钱.
选一些具体数字,通过计算验证你的发现是否正确.
当t大于350 时,按方式一
的计费 58+0.25(t-150)
可变 形为 108 + 0.25(t - 350).对比按方式二 的计费,你能说明此 时按哪种方式的计费少吗?
t<270
t>270
解答这类问题的一般步骤:
1.运用一元一次方程解应用题的方法,求解使方案值相等的情况;
2.用特殊值试探去选择方案,取小于(或大于)一元一次方程解 的值,比较两种方案的优劣后下结论.
例1 某市上网有两种收费方案,用户可任选其一:A为计时制——1元/时;B为包月制——80元/月,此外每种上网方式都附加通讯费0.1元/时.
(1)某用户每月上网40小时,选哪种方式比较合算?
(2)某用户每月有110元钱用于上网,选哪种方式比较合算?
(3)请你设计一个方案,使用户能合理地选择上网方式.
导引:(1)提供了上网时间40小时,根据“单价×总时长=总价”,求出A,B收费方案下的费用,进行比较;(2)提供了上网的总费用,已知上网的单价,求出总时长进行比较;(3)根据用户的上网时长,比较哪种方案收费较少,帮其设计合理的方案.
解:(1)如果用户每月上网40小时:
A计时制:40×(0.1+1)=44(元),
B包月制:80+40×0.1=84(元),
44<84,故选A计时制比较合算.
(2)设用户用110元上网,A计时制可上网x小时,
B包月制可上网y小时,
则(1+0.1)x=110,解得x=100,
80+0.1 y=110,解得y =300.
因为100<300,故选B包月制比较合算.
(3)设用户上网z小时,两种方式收费一样多.
则(1+0.1)z=80+0.1z.
解得z=80.
故上网不足80小时,选A计时制;
上网超过80小时,选B包月制;
上网恰好80小时,两种方案都一样.
B
1
张老师一家三口暑假准备参加旅游团去北京旅游,甲旅行社说:“如果父母买全票,小孩可半价优惠”;乙旅行社说:“全部按全票价的8折优惠”,若全票价为1 200元.则张老师应选择哪家旅行社?( )
A.选择甲 B.选择乙
C.选择甲、乙都一样 D.无法确定
2
某校准备为毕业班学生制作一批纪念册.甲公司提出:每册收材料费5元,另收设计费1 500元;乙公司提出:每册收材料费8元,不收设计费.张老师经过计算,发现两家公司收费一样,则该校今年毕业生有_______人.
500
2
知识点
分段计费问题
例2 近几年我国部分地区不时出现的严重干旱,使我们认识 到节水的重要性.为了加强公民的节水意识,合理利用水资源,某市对自来水收费采用阶梯价格的调控手段以达到节水的目的.
该市自来水收费价格见价目表.
价目表
每月用水量 单价
不超出6 m3的部分 2元/m3
超出6 m3但不超出10 m3的部分 4元/m3
超出10 m3的部分 8元/m3
注:水费按月结算
(1)若某户居民2月份用水10.5 m3,应交水费多少元?
(2)若该户居民3,4月份共用水16 m3(4月份用水量超过3月份),共交水费44元,则该户居民3,4月份各用水多少立方米?(结果精确到0.1 m3)
解:(1)由题意,得2×6+4×(10-6)+8×(10.5-10)=32(元).
所以二月份应交水费32元.
(2)设三月份用水x m3,则四月份用水(16-x) m3.
①当x≤6时,16-x≥10,
依题意,得2x+2×6+4×4+8(16-x-10)=44.
整理,得6x=32,所以x≈5.3,此时16-x≈10.7,符合题意.
②当6<x≤10时,6≤16-x<10,依题意,
得2×6+4×(x-6)+2×6+4(16-x-6)=44.
整理,得40=44,此方程无解.所以6<x≤10不可能成立.
③因为4月份用水量超过3月份,所以x不可能超过10.
综上所述,三月份用水约5.3 m3,四月份用水约10.7 m3.
1
参加保险公司的医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表:
住院医疗费 报销率(%)
不超过500元的部分 0
超过500~1 000元的部分 60
超过1 000~3 000元的部分 80
… …
D
某人住院治疗后得到保险公司报销金额是1 100元,那么此人住院的医疗费是( )
A.1 000元 B.1 250元
C.1 500元 D.2 000元
谈谈本节课学到了哪些知识?学后有何感受?
请完成对应习题
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
