沪科版七上数学第3章3.2行程问题 教学课件(34张PPT)
文档属性
| 名称 | 沪科版七上数学第3章3.2行程问题 教学课件(34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 757.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 15:32:42 | ||
图片预览









文档简介
(共34张PPT)
第3章 一次方程与方程组
3.2 一元一次方程的应用
行程问题
1
课堂讲解
一般行程问题
顺流(风)、逆流(风)问题
上坡、下坡问题
2
课时流程
逐点
导讲练
课堂小结
课后作业
1
知识点
一般行程问题
1.行程问题的基本关系式:
路程=速度×时间,
时间=路程÷速度,
速度=路程÷时间.
2.行程问题中的等量关系:
(1)相遇问题中的等量关系:
①甲走的路程+乙走的路程=甲、乙出发点之间的路程;
②若甲、乙同时出发,甲用的时间=乙用的时间.
(2)追及问题中的等量关系:
①快者走的路程-慢者走的路程=追及路程;
②若同时出发,快者追上慢者时,快者用的时间=慢者用的时间.
例1 为了适应经济发展,铁路运输再次提速.如果客车行驶的平均速度增加40 km/h,提速后由合肥到北京1 110 km的路程只需行驶10 h.那么,提速前,这趟客车平均每时行驶多少千米?
分析:行程问题中常涉及的量有路程、平均速度、时间. 它们之间的基本关系是:路程=平均速度×时间.
解:设提速前客车平均每时行驶x km,那么提速后客车平均每时行驶(x+40) km.客车行驶路程1 110 km,平均速度是(x+40) km/h,所需时间是10 h.根据题意,得10(x+40)=1 110.
解方程,得 x=71.
答:提速前这趟客车的平均速度是71 km/h.
例2 甲站和乙站相距1 500 km,一列慢车从甲站开出,速度为60 km/h,一列快车从乙站开出,速度为90 km/h.
(1)若两车相向而行,慢车先开30 min,快车开出几小时后两车相遇?
(2)若两车同时开出,相背而行,多少小时后两车相距1 800 km?
(3)若两车同时开出,快车在慢车后面同向而行,多少小时后两车相距1 200 km(此时快车在慢车的后面)?
导引:(1)列表:
等量关系:慢车行驶的路程+快车行驶的路程=1 500 km.
路程/km 速度/(km/h) 时间/h
慢车 60 60 x +
快车 90x 90 x
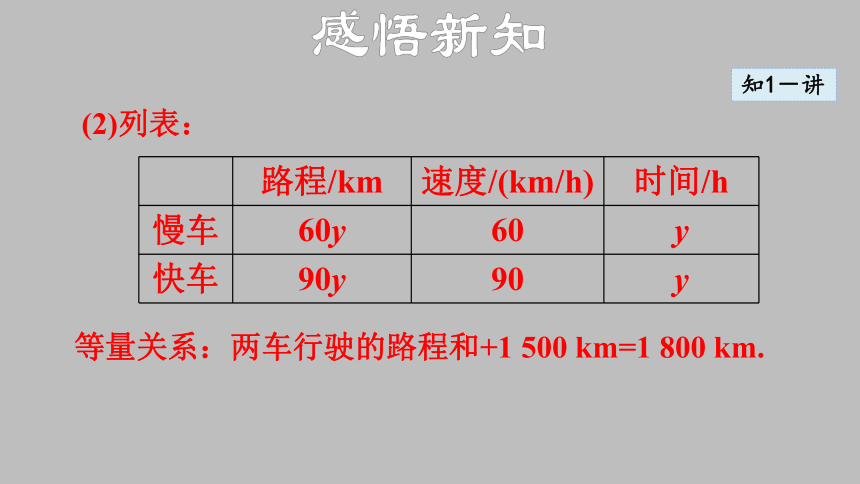
(2)列表:
等量关系:两车行驶的路程和+1 500 km=1 800 km.
路程/km 速度/(km/h) 时间/h
慢车 60y 60 y
快车 90y 90 y
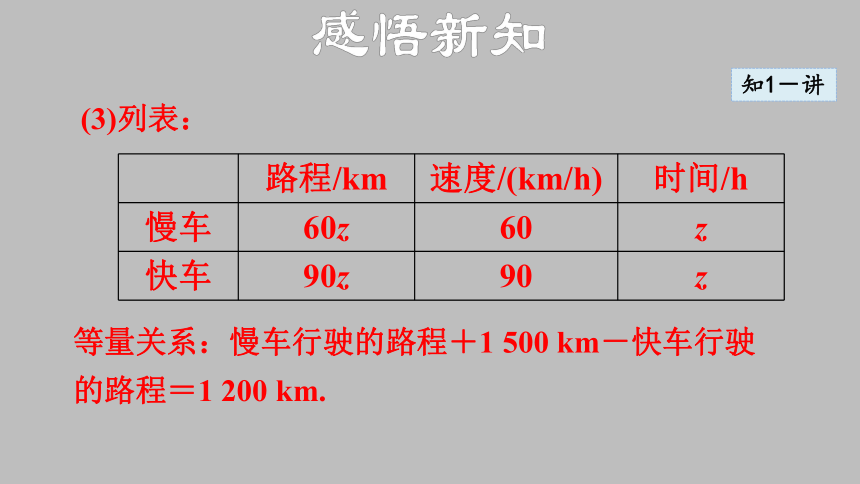
(3)列表:
等量关系:慢车行驶的路程+1 500 km-快车行驶的路程=1 200 km.
路程/km 速度/(km/h) 时间/h
慢车 60z 60 z
快车 90z 90 z
解:(1)设快车开出x h后两车相遇.
由题意,得60× +90x=1 500.
解得x=9.8.
答:快车开出9.8 h后两车相遇.
(2)设y h后两车相距1 800 km.
由题意,得60y+90y+1 500=1 800.解得y=2.
答:2 h后两车相距1 800 km.
(3)设z h后两车相距1 200 km(此时快车在慢车的后面).
由题意,得60z+1 500-90z=1 200.解得z=10.
答:10 h后两车相距1 200 km(此时快车在慢车的后面).
(1)行程问题中,可借助图示、列表来分析数量关系,图示可直观地找出路程等量关系,列表可将路程、速度、时间的关系清晰地展示出来.
(2)本例是求时间,我们可设时间为未知数,从表中求路程;
如果要求的是路程,那么我们可设路程为未知数,从表中求时间,其依据是路程、速度和时间三者间的关系式.如(1)小题若将“几小时后两车相遇?”改为“相遇时快车走了多少千米?”若设间接未知数,则原导引及解不变,只是将x求出后,再求出90x的值即可,若设直接未知数,则导引改为:
列表:
等量关系:慢车行驶时间- h=快车行驶时间.
方程为:
路程/km 速度/(km/h) 时间/h
慢车 1500-x 60
快车 x 90
(3)一般规律:在路程、速度、时间这三个量中,甲量已知,从乙量设元,则从丙量中找相等关系列方程;在所有行程问题中,一般都已知一个量,另两个量相互之间都存在关系.
易错警示:
单位不统一是行程问题最易出现的错误,本例中速度单位是km/h,而(1)小题中出现的时间单位是min,解题时需把30min化为
例3 小明和他的哥哥早晨起来沿长为400 m的环形跑道练习跑步,小明跑2圈用的时间和他的哥哥跑3圈用的时间相等,两人同时同地同向出发,经过2 min 40 s他们第一次相遇,若他们两人同时同地反向出发,则经过几秒他们第一次相遇?
导引:列表:
相等关系:小明跑的路程=哥哥跑的路程-400 m.
路程/m 速度/m/s 时间/s
小明 160x x 160
哥哥 160× 160
解:设小明的速度为x m/s,则他的哥哥的速度为
由题意得:160x=160×
解得x=5.则小明的哥哥的速度为5×
设经过y s他们第一次相遇,由题意,得:
(5+7.5)y=400.
解得y=32.
答:经过32 s他们第一次相遇.
(1)本例在求小明及哥哥的速度时,也可设他们两人
的速度分别为2x m/s和3x m/s.
(2)环形运动问题中的等量关系(同时同地出发):①
同向相遇:第一次相遇时快者的路程-第一次相
遇时慢者的路程=跑道一圈的长度;②反向相遇:
第一次相遇时快者的路程+第一次相遇时慢者的
路程=跑道一圈的长度.
1
甲、乙两人在一环形公路上骑自行车,环形公路长为42 km,甲、乙两人的速度分别为21 km/h、
14 km/h.
(1)如果两人从公路的同一地点同时反向出发,那么经几小时后,两人首次相遇?
(2)如果两人从公路的同一地点同时同向出发,那么出发后经几小时两人第二次相遇?
解:(1)设经过x h后,则两人首次相遇。
依题意,得21x+14x=42. 解得x=1.2 .
答:经过1.2h后,两人首次相遇.
(2)设出发yh两人二次相遇.
依题意,得21y-14y=42×2,解得y=12.
答:出发后经12h两人第二次相遇,
2
知识点
顺流(风)、逆流(风)问题
顺流(风)、逆流(风)问题:船在静水中的
速度记为v静,水的速度记为v水,船在顺水中的速度记为v顺,船在逆水中的速度记为v逆,则
v顺=v静+v水,v逆=v静-v水.
例4 一艘船从甲码头到乙码头顺流行驶用4小时,从乙码头到甲码头逆流行驶用4小时40分钟,已知水流速度为3千米/小时,则船在静水中的平均速度是多少?
解:设船在静水中的平均速度是x千米/小时,
根据题意,得4(x+3)=
解得x=39.
答:船在静水中的平均速度是39千米/小时.
3
知识点
上坡、下坡问题
例5 (中考·株洲)家住山脚下的孔明同学想从家发登山游玩,据以往的经验,他获得如下信息:
(1)他下山时的速度比上山时的速度每小时快1千米;
(2)他上山2小时到达的位置,离山顶还有1千米;
(3)抄近路下山,下山路程比上山路程近2千米;
(4)下山用1个小时.
根据上面信息,他做出如下计划:
(1)在山顶游览1个小时;
(2)中午12:00回到家吃中餐.
若依据以上信息和计划登山游玩,
请问:孔明同学应在什么时间从家出发?
解:设上山的速度为v千米/小时,下山的速度为(v+1)千米/小时,
则2v+1=v+1+2,
解得v=2.
即上山速度是2千米/小时.
则下山的速度是3千米/小时,上山的路程为5千米.
则计划上山的时间为:5÷2=2.5(小时),
计划下山的时间为:1小时,
则共用时间为:2.5+1+1=4.5(小时),
所以出发时间为12:00-4小时30分钟=7:30.
答:孔明同学应该在7:30分从家出发.
行程问题有相遇问题,追及问题,顺流、逆流问题,上坡、下坡问题等.在运动形式上分直线运动及曲线运动(如环形跑道).相遇问题是相向而行,相遇时的总路程为两运动物体的路程和.追及问题是同向而行,分慢的在快的前面或慢的先行若干时间,快的再追.顺流、逆流、顺风、逆风、上下坡应注意运动方向.
请完成对应习题
第3章 一次方程与方程组
3.2 一元一次方程的应用
行程问题
1
课堂讲解
一般行程问题
顺流(风)、逆流(风)问题
上坡、下坡问题
2
课时流程
逐点
导讲练
课堂小结
课后作业
1
知识点
一般行程问题
1.行程问题的基本关系式:
路程=速度×时间,
时间=路程÷速度,
速度=路程÷时间.
2.行程问题中的等量关系:
(1)相遇问题中的等量关系:
①甲走的路程+乙走的路程=甲、乙出发点之间的路程;
②若甲、乙同时出发,甲用的时间=乙用的时间.
(2)追及问题中的等量关系:
①快者走的路程-慢者走的路程=追及路程;
②若同时出发,快者追上慢者时,快者用的时间=慢者用的时间.
例1 为了适应经济发展,铁路运输再次提速.如果客车行驶的平均速度增加40 km/h,提速后由合肥到北京1 110 km的路程只需行驶10 h.那么,提速前,这趟客车平均每时行驶多少千米?
分析:行程问题中常涉及的量有路程、平均速度、时间. 它们之间的基本关系是:路程=平均速度×时间.
解:设提速前客车平均每时行驶x km,那么提速后客车平均每时行驶(x+40) km.客车行驶路程1 110 km,平均速度是(x+40) km/h,所需时间是10 h.根据题意,得10(x+40)=1 110.
解方程,得 x=71.
答:提速前这趟客车的平均速度是71 km/h.
例2 甲站和乙站相距1 500 km,一列慢车从甲站开出,速度为60 km/h,一列快车从乙站开出,速度为90 km/h.
(1)若两车相向而行,慢车先开30 min,快车开出几小时后两车相遇?
(2)若两车同时开出,相背而行,多少小时后两车相距1 800 km?
(3)若两车同时开出,快车在慢车后面同向而行,多少小时后两车相距1 200 km(此时快车在慢车的后面)?
导引:(1)列表:
等量关系:慢车行驶的路程+快车行驶的路程=1 500 km.
路程/km 速度/(km/h) 时间/h
慢车 60 60 x +
快车 90x 90 x
(2)列表:
等量关系:两车行驶的路程和+1 500 km=1 800 km.
路程/km 速度/(km/h) 时间/h
慢车 60y 60 y
快车 90y 90 y
(3)列表:
等量关系:慢车行驶的路程+1 500 km-快车行驶的路程=1 200 km.
路程/km 速度/(km/h) 时间/h
慢车 60z 60 z
快车 90z 90 z
解:(1)设快车开出x h后两车相遇.
由题意,得60× +90x=1 500.
解得x=9.8.
答:快车开出9.8 h后两车相遇.
(2)设y h后两车相距1 800 km.
由题意,得60y+90y+1 500=1 800.解得y=2.
答:2 h后两车相距1 800 km.
(3)设z h后两车相距1 200 km(此时快车在慢车的后面).
由题意,得60z+1 500-90z=1 200.解得z=10.
答:10 h后两车相距1 200 km(此时快车在慢车的后面).
(1)行程问题中,可借助图示、列表来分析数量关系,图示可直观地找出路程等量关系,列表可将路程、速度、时间的关系清晰地展示出来.
(2)本例是求时间,我们可设时间为未知数,从表中求路程;
如果要求的是路程,那么我们可设路程为未知数,从表中求时间,其依据是路程、速度和时间三者间的关系式.如(1)小题若将“几小时后两车相遇?”改为“相遇时快车走了多少千米?”若设间接未知数,则原导引及解不变,只是将x求出后,再求出90x的值即可,若设直接未知数,则导引改为:
列表:
等量关系:慢车行驶时间- h=快车行驶时间.
方程为:
路程/km 速度/(km/h) 时间/h
慢车 1500-x 60
快车 x 90
(3)一般规律:在路程、速度、时间这三个量中,甲量已知,从乙量设元,则从丙量中找相等关系列方程;在所有行程问题中,一般都已知一个量,另两个量相互之间都存在关系.
易错警示:
单位不统一是行程问题最易出现的错误,本例中速度单位是km/h,而(1)小题中出现的时间单位是min,解题时需把30min化为
例3 小明和他的哥哥早晨起来沿长为400 m的环形跑道练习跑步,小明跑2圈用的时间和他的哥哥跑3圈用的时间相等,两人同时同地同向出发,经过2 min 40 s他们第一次相遇,若他们两人同时同地反向出发,则经过几秒他们第一次相遇?
导引:列表:
相等关系:小明跑的路程=哥哥跑的路程-400 m.
路程/m 速度/m/s 时间/s
小明 160x x 160
哥哥 160× 160
解:设小明的速度为x m/s,则他的哥哥的速度为
由题意得:160x=160×
解得x=5.则小明的哥哥的速度为5×
设经过y s他们第一次相遇,由题意,得:
(5+7.5)y=400.
解得y=32.
答:经过32 s他们第一次相遇.
(1)本例在求小明及哥哥的速度时,也可设他们两人
的速度分别为2x m/s和3x m/s.
(2)环形运动问题中的等量关系(同时同地出发):①
同向相遇:第一次相遇时快者的路程-第一次相
遇时慢者的路程=跑道一圈的长度;②反向相遇:
第一次相遇时快者的路程+第一次相遇时慢者的
路程=跑道一圈的长度.
1
甲、乙两人在一环形公路上骑自行车,环形公路长为42 km,甲、乙两人的速度分别为21 km/h、
14 km/h.
(1)如果两人从公路的同一地点同时反向出发,那么经几小时后,两人首次相遇?
(2)如果两人从公路的同一地点同时同向出发,那么出发后经几小时两人第二次相遇?
解:(1)设经过x h后,则两人首次相遇。
依题意,得21x+14x=42. 解得x=1.2 .
答:经过1.2h后,两人首次相遇.
(2)设出发yh两人二次相遇.
依题意,得21y-14y=42×2,解得y=12.
答:出发后经12h两人第二次相遇,
2
知识点
顺流(风)、逆流(风)问题
顺流(风)、逆流(风)问题:船在静水中的
速度记为v静,水的速度记为v水,船在顺水中的速度记为v顺,船在逆水中的速度记为v逆,则
v顺=v静+v水,v逆=v静-v水.
例4 一艘船从甲码头到乙码头顺流行驶用4小时,从乙码头到甲码头逆流行驶用4小时40分钟,已知水流速度为3千米/小时,则船在静水中的平均速度是多少?
解:设船在静水中的平均速度是x千米/小时,
根据题意,得4(x+3)=
解得x=39.
答:船在静水中的平均速度是39千米/小时.
3
知识点
上坡、下坡问题
例5 (中考·株洲)家住山脚下的孔明同学想从家发登山游玩,据以往的经验,他获得如下信息:
(1)他下山时的速度比上山时的速度每小时快1千米;
(2)他上山2小时到达的位置,离山顶还有1千米;
(3)抄近路下山,下山路程比上山路程近2千米;
(4)下山用1个小时.
根据上面信息,他做出如下计划:
(1)在山顶游览1个小时;
(2)中午12:00回到家吃中餐.
若依据以上信息和计划登山游玩,
请问:孔明同学应在什么时间从家出发?
解:设上山的速度为v千米/小时,下山的速度为(v+1)千米/小时,
则2v+1=v+1+2,
解得v=2.
即上山速度是2千米/小时.
则下山的速度是3千米/小时,上山的路程为5千米.
则计划上山的时间为:5÷2=2.5(小时),
计划下山的时间为:1小时,
则共用时间为:2.5+1+1=4.5(小时),
所以出发时间为12:00-4小时30分钟=7:30.
答:孔明同学应该在7:30分从家出发.
行程问题有相遇问题,追及问题,顺流、逆流问题,上坡、下坡问题等.在运动形式上分直线运动及曲线运动(如环形跑道).相遇问题是相向而行,相遇时的总路程为两运动物体的路程和.追及问题是同向而行,分慢的在快的前面或慢的先行若干时间,快的再追.顺流、逆流、顺风、逆风、上下坡应注意运动方向.
请完成对应习题
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
