沪科版七上数学3.5 三元一次方程组及其解法教学课件(42张)
文档属性
| 名称 | 沪科版七上数学3.5 三元一次方程组及其解法教学课件(42张) |

|
|
| 格式 | zip | ||
| 文件大小 | 802.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 00:00:00 | ||
图片预览









文档简介
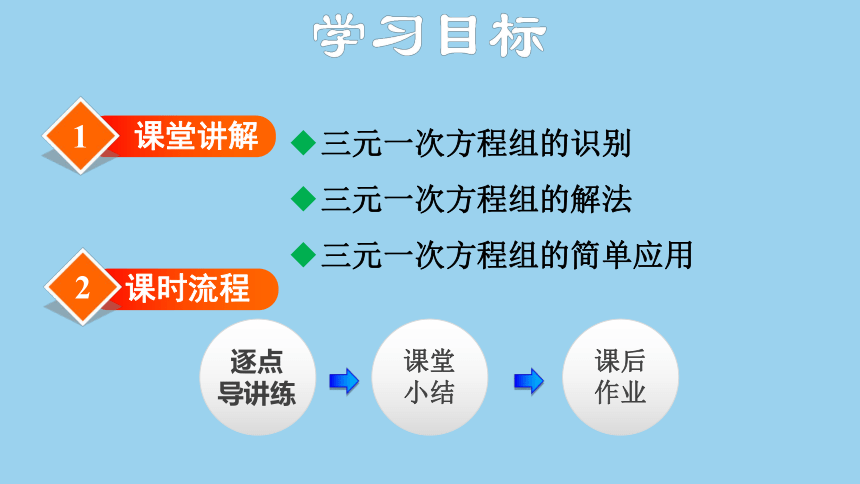
(共42张PPT)
第3章 一次方程与方程组
3.5 三元一次方程组及其解法
1
课堂讲解
三元一次方程组的识别
三元一次方程组的解法
三元一次方程组的简单应用
2
课时流程
逐点
导讲练
课堂小结
课后作业
1
知识点
三元一次方程组的识别
1.三元一次方程:含有三个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做三元一次方程.
必备条件:(1)是整式方程;(2)含三个未知数; (3)含未知数的项的次数都是1.
2.三元一次方程组:由三个一次方程组成的含有三个未知数的方程组叫做三元一次方程组.
例1 下列方程组中,是三元一次方程组的是( )
D
满足三元一次方程组的条件:
(1)方程组中一共含有三个未知数:
(2)每个方程中含未知数的项的次数都是1;
(3)方程组中共有三个整式方程.
①
下列方程是三元一次方程的是________.(填序号)
①x+y-z=1 ②4xy+3z=7
③ +y-7z=0 ④6x+4y-3=0
1
① ② ③
2
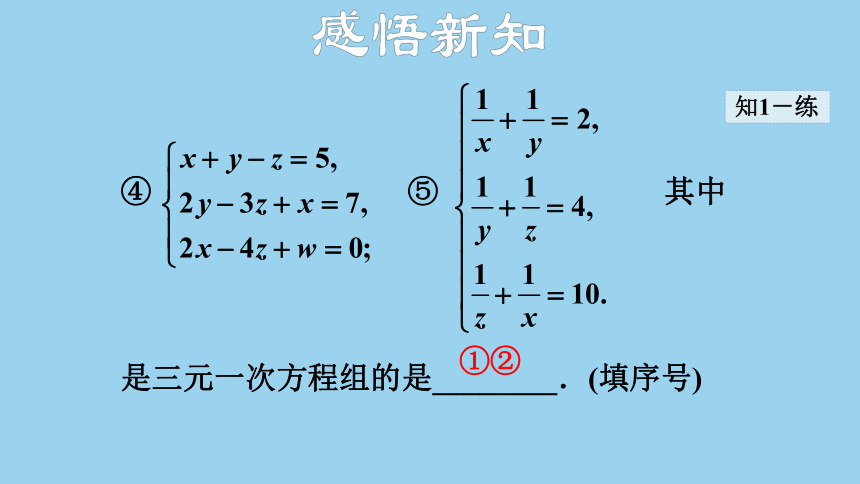
①②
④ ⑤ 其中是三元一次方程组的是________.(填序号)
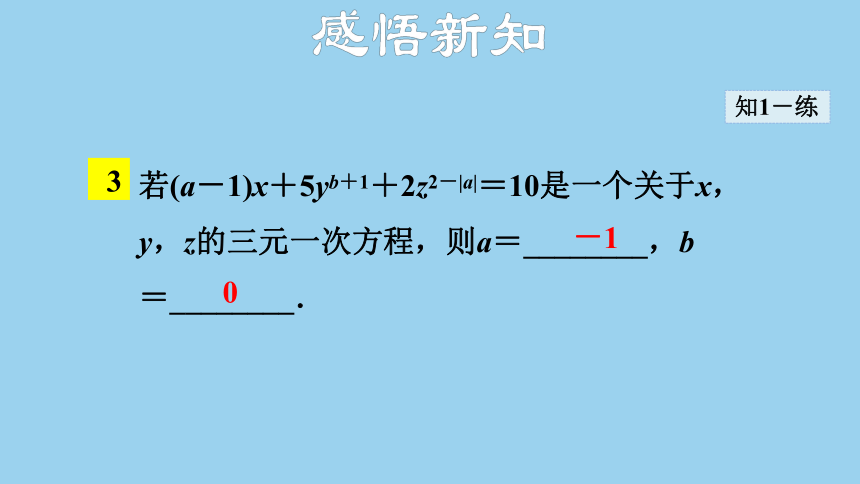
若(a-1)x+5yb+1+2z2-|a|=10是一个关于x,y,z的三元一次方程,则a=________,b=________.
3
-1
0
2
知识点
三元一次方程组的解法
1.解三元一次方程组的基本思路是:通过“代入” 或“加减”进行消元,把“三元”化为“二元”,把三元一次方程组转化为二元一次方程组,进而再转化为一元一次方程,用简图表示为:
三元一次方程组
消元
二元一次方程组
消元
一元一次方程组
2.求解方法:加减消元法和代入消元法.
3.解三元一次方程组的一般步骤:
(1)利用代入法或加减法消去三元一次方程组的一个未知数,得到关于另外两个未知数的二元一次方程组;
(2)解这个二元一次方程组,求出两个未知数的值;
(3)将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个一元一次方程;
(4)解这个一元一次方程,求出最后一个未知数的值;
(5)将求得的三个未知数的值用符号“{”合写在一起.
例2 解方程组:
①
②
③
解:先用加减消元法消去x:
② +①×2,得y+5z =3. ④
③-①,得y -6z = -8. ⑤
下面解由④ ⑤联立成的二元一次方程组:
④-⑤,得11z=11. ⑥
所以z=1. ⑦
将⑦代入④,得y=-2.
将y, z的值代入① ,得x=3.
所以
例3 解《九章算术》第八章第一题的方程组:
①
②
③
解:将方程③前移为第1个方程,将方程①和②分别后移为第2个和第3个方程,得
⑥
④
⑤
⑤-④×3,⑥-④×2,得
④
⑦
⑧
⑧+⑦× ,得
再通过回代,解得
所以
1
解下列方程组:
解三元一次方程组
先消去________,化为关于________,________的二元一次方程组再求解较简便.
2
z
x
y
B
解方程组
若要使运算简便,消元的方法应选( )
A.消去x B.消去y
C.消去z D.以上说法都不对
3
已知三元一次方程组
经过步骤①-③和③×4+②消去未知数z后,得到的二元一次方程组是( )
①
②
③
4
A. B.
C. D.
√
3
知识点
三元一次方程组的简单应用
例4 幼儿营养标准中要求一个幼儿每天所需的养量中应包含35单位的铁、70单位的钙和35单位的维 生素.现有一营养师根据上面的标准给幼儿园小朋友们 配餐,其中包含A,B,C三种食物,下表给出的是每份 (50g)食物A,B,C分别所含的铁、钙和维生素的量 (单位).
食物 铁 钙 维生素
A 5 20 5
B 5 10 15
C 10 10 5
(1)如果设食谱中A,B, C三种食物各为x, y, z份, 请列出方程组,使得A, B,C三种食物中所含的营养量刚 好满足幼儿营养标准中的要求.
(2)解该三元一次方程组,求出满足要求的A,B,C的份数.
解: (1)设食谱中A,B,C三种食物各为x, y,z份, 由该食谱中包含35单位的铁、70单位的钙和35单位的维生素,得方程组
?
?
①
②
③
(2)②-①×4,③-①,得
①
④
⑤
⑤+④,得
①
④
⑥
你还有其他解法吗?
再通过回代,
解得 z = 2,y = l,x =2.
答:该食谱中包含A种食物2份,
B种食物1份,C种 食物2份.
120
(中考·滨州)某服装厂专门安排210名工人进行手工衬衣的缝制,每件衬衣由2个衣袖、1个衣身、1个衣领组成.如果每人每天能够缝制衣袖10个,或衣身15个,或衣领12个,那么应该安排______名工人缝制衣袖,才能使每天缝制出的衣袖、衣身、衣领正好配套.
1
某商场计划用60 000元从某厂家购进若干部新型手机,以满足市场需求.已知该厂家 生产的甲、乙、丙三种型号手机,出厂价分别为每部1 800元、600元和1 200元.该商场 用60 000元恰好购买上述三种型号手机共40部,因市场需求甲型号手机比丙型号手 机多购买了24部,求该商场购买了上述三种型号手机各多少部?
2
解: (1)设购买了甲、乙、丙三种手机的数量分别为x, y,z部, 由题意可得方程组?
由③得x=24+z,④
将④代入②,得y=16-2z,⑤
将④、⑤代入①,解得z=4.
由④得x=28,
由⑤得y=8.
答: 该商场购买了甲型号手机28部,乙型号手机8部,丙型号手机4部.
三元一次方程组的必备条件:
(1)是整式方程;(2)含三个未知数;(3)三个都是一次方程;(4)联立在一起.
解三元一次方程组的基本思路仍是消元,是将复杂问题简单化的一种方法.其目的是利用代入法或加减法消去一个未知数,从而变三元为二元,然后解这个二元一次方程组,求出两个未知数,最后再求出另一个未知 数.
其基本过程为:三元 二元 一元.
消元
转化
消元
转化
请完成对应习题
第3章 一次方程与方程组
3.5 三元一次方程组及其解法
1
课堂讲解
三元一次方程组的识别
三元一次方程组的解法
三元一次方程组的简单应用
2
课时流程
逐点
导讲练
课堂小结
课后作业
1
知识点
三元一次方程组的识别
1.三元一次方程:含有三个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做三元一次方程.
必备条件:(1)是整式方程;(2)含三个未知数; (3)含未知数的项的次数都是1.
2.三元一次方程组:由三个一次方程组成的含有三个未知数的方程组叫做三元一次方程组.
例1 下列方程组中,是三元一次方程组的是( )
D
满足三元一次方程组的条件:
(1)方程组中一共含有三个未知数:
(2)每个方程中含未知数的项的次数都是1;
(3)方程组中共有三个整式方程.
①
下列方程是三元一次方程的是________.(填序号)
①x+y-z=1 ②4xy+3z=7
③ +y-7z=0 ④6x+4y-3=0
1
① ② ③
2
①②
④ ⑤ 其中是三元一次方程组的是________.(填序号)
若(a-1)x+5yb+1+2z2-|a|=10是一个关于x,y,z的三元一次方程,则a=________,b=________.
3
-1
0
2
知识点
三元一次方程组的解法
1.解三元一次方程组的基本思路是:通过“代入” 或“加减”进行消元,把“三元”化为“二元”,把三元一次方程组转化为二元一次方程组,进而再转化为一元一次方程,用简图表示为:
三元一次方程组
消元
二元一次方程组
消元
一元一次方程组
2.求解方法:加减消元法和代入消元法.
3.解三元一次方程组的一般步骤:
(1)利用代入法或加减法消去三元一次方程组的一个未知数,得到关于另外两个未知数的二元一次方程组;
(2)解这个二元一次方程组,求出两个未知数的值;
(3)将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个一元一次方程;
(4)解这个一元一次方程,求出最后一个未知数的值;
(5)将求得的三个未知数的值用符号“{”合写在一起.
例2 解方程组:
①
②
③
解:先用加减消元法消去x:
② +①×2,得y+5z =3. ④
③-①,得y -6z = -8. ⑤
下面解由④ ⑤联立成的二元一次方程组:
④-⑤,得11z=11. ⑥
所以z=1. ⑦
将⑦代入④,得y=-2.
将y, z的值代入① ,得x=3.
所以
例3 解《九章算术》第八章第一题的方程组:
①
②
③
解:将方程③前移为第1个方程,将方程①和②分别后移为第2个和第3个方程,得
⑥
④
⑤
⑤-④×3,⑥-④×2,得
④
⑦
⑧
⑧+⑦× ,得
再通过回代,解得
所以
1
解下列方程组:
解三元一次方程组
先消去________,化为关于________,________的二元一次方程组再求解较简便.
2
z
x
y
B
解方程组
若要使运算简便,消元的方法应选( )
A.消去x B.消去y
C.消去z D.以上说法都不对
3
已知三元一次方程组
经过步骤①-③和③×4+②消去未知数z后,得到的二元一次方程组是( )
①
②
③
4
A. B.
C. D.
√
3
知识点
三元一次方程组的简单应用
例4 幼儿营养标准中要求一个幼儿每天所需的养量中应包含35单位的铁、70单位的钙和35单位的维 生素.现有一营养师根据上面的标准给幼儿园小朋友们 配餐,其中包含A,B,C三种食物,下表给出的是每份 (50g)食物A,B,C分别所含的铁、钙和维生素的量 (单位).
食物 铁 钙 维生素
A 5 20 5
B 5 10 15
C 10 10 5
(1)如果设食谱中A,B, C三种食物各为x, y, z份, 请列出方程组,使得A, B,C三种食物中所含的营养量刚 好满足幼儿营养标准中的要求.
(2)解该三元一次方程组,求出满足要求的A,B,C的份数.
解: (1)设食谱中A,B,C三种食物各为x, y,z份, 由该食谱中包含35单位的铁、70单位的钙和35单位的维生素,得方程组
?
?
①
②
③
(2)②-①×4,③-①,得
①
④
⑤
⑤+④,得
①
④
⑥
你还有其他解法吗?
再通过回代,
解得 z = 2,y = l,x =2.
答:该食谱中包含A种食物2份,
B种食物1份,C种 食物2份.
120
(中考·滨州)某服装厂专门安排210名工人进行手工衬衣的缝制,每件衬衣由2个衣袖、1个衣身、1个衣领组成.如果每人每天能够缝制衣袖10个,或衣身15个,或衣领12个,那么应该安排______名工人缝制衣袖,才能使每天缝制出的衣袖、衣身、衣领正好配套.
1
某商场计划用60 000元从某厂家购进若干部新型手机,以满足市场需求.已知该厂家 生产的甲、乙、丙三种型号手机,出厂价分别为每部1 800元、600元和1 200元.该商场 用60 000元恰好购买上述三种型号手机共40部,因市场需求甲型号手机比丙型号手 机多购买了24部,求该商场购买了上述三种型号手机各多少部?
2
解: (1)设购买了甲、乙、丙三种手机的数量分别为x, y,z部, 由题意可得方程组?
由③得x=24+z,④
将④代入②,得y=16-2z,⑤
将④、⑤代入①,解得z=4.
由④得x=28,
由⑤得y=8.
答: 该商场购买了甲型号手机28部,乙型号手机8部,丙型号手机4部.
三元一次方程组的必备条件:
(1)是整式方程;(2)含三个未知数;(3)三个都是一次方程;(4)联立在一起.
解三元一次方程组的基本思路仍是消元,是将复杂问题简单化的一种方法.其目的是利用代入法或加减法消去一个未知数,从而变三元为二元,然后解这个二元一次方程组,求出两个未知数,最后再求出另一个未知 数.
其基本过程为:三元 二元 一元.
消元
转化
消元
转化
请完成对应习题
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
