高中数学人教B版选修2-2 第一章 1.4.1曲边梯形的面积与定积分 上课课件(共32张PPT)
文档属性
| 名称 | 高中数学人教B版选修2-2 第一章 1.4.1曲边梯形的面积与定积分 上课课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-19 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
定积分:以直代曲,用“均匀”的研究“不均匀”的;用无限的方法研究有限的问题,从局部到整体.
具体实例:曲边梯形的面积、变速直线运动的路程.
1.4 定积分与微积分基本定理
有什么思路吗?
新课导入
中学学习过:三角形,圆形,矩形,平行四边形,梯形等规则图形面积的计算,而计算平面曲线围成的平面“曲边图形”的面积、变速直线运动物体位移、变力做功等问题.
如何解决这些实际问题呢?
能否把求“曲边图形”面积转化为求“直边图形”面积?能否利用匀速直线运动的知识解决变速直线运动的问题?为此,我们需要学习新的数学知识—— .
定积分
a
b
x
y
o
1.4.1 曲边梯形面积与定积分
曲边梯形的面积怎么求?
教学目标
知识与能力
能根据正多边形逼近圆的面积而求出圆面积的过程,概括出求平面曲边梯形面积的基本思想:在每个局部小范围内“以直代曲”和逼近的思想.
过程与方法
(1)根据“以直代曲”和“逼近”的思想将求曲线梯形面积化为四个步骤:分割、近似代替、求和、取极限.
(2)了解定积分概念中蕴涵的最本质的思想.
情感态度与价值观
利用计算平面“曲边图形”的面积,从实际问题引发学生学习定积分知识的欲望.
教学重难点
重点
“以直代曲”和“以不变代变”的思想方法.
难点
“以直代曲”和“以不变代变”的思想方法.
一般地,如果函数 在某个区间 上的图象是一条连续不断的曲线,那么我们就把它称为区间 上的连续函数.例如
知识点!
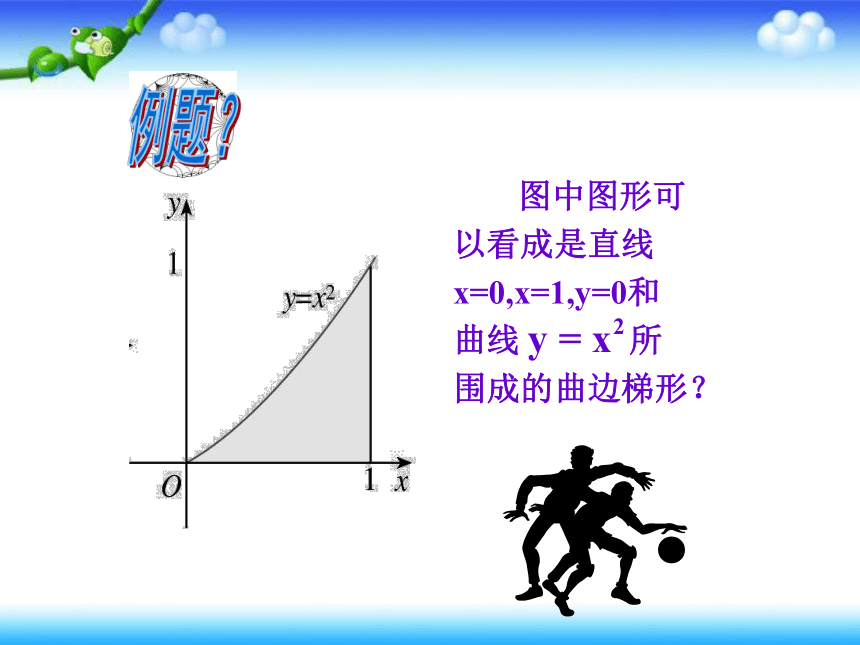
图中图形可以看成是直线x=0,x=1,y=0和曲线 所围成的曲边梯形?
例题?
思考?
图中的曲边梯形与我们熟悉的“直边图形”的主要区别是什么?能否将求这个曲边梯形面积s的问题转化为求“直边图形”面积的问题?
在过去的学习中,我们曾用正多边形逼近圆的方法,利用正多边形面积求圆的面积.
用这种“以直代曲”的思想启发我们!
发现!
发现!
曲边梯形与“直边图形”的主要区别是,前者有一边是曲线段,而“直边图形”的所有边都是直线段.
是否也能用直边形(比如矩形)逼近曲边梯形的方法求阴影部分面积?
观察下列演示过程,注意当分割加细时,矩形面积和与曲边梯形面积的关系.
对每个小曲边梯形“以直代曲”,即用矩形的面积近似代替小曲边梯形的面积,得到每个小曲边梯形面积的近似值,对这些近似值求和,就得到曲边梯形面积的近似值.
即用化归为计算矩形面积和逼近的思想方法求出曲边梯形的面积.
在区间[0,1]中任意插入n-1个分点:
把[0,1]分成n个小区间[xi-1, xi] (i=n-1)区间长度为 (i=n-1)
分割:
如图,当n很大时,即△x很小时,在区间 上可以认为函数 的值变化很小.
近似代替:
把曲边梯形分成n个小曲边梯形面积记做 .用小矩形的面积 近似地替代 ,即局部小范围内“以直代曲”.
则阴影部分面积
求和:
得到S(曲边梯形)的近似值:
取极限:
当n趋向于无穷大
当n趋向于无穷大,即 趋向于0时, 趋向于S.从而有
在“近似代替”中,如果认为函数 在区间 上的值近似地等于右端点 处的函数值 ,用这种方法能求出S的值吗?若能求出,这个值也是 吗?取任意 处的函数值 作为近似值,情况又怎样?
探究!
可以证明,取 在区间 上任意一点 处的值 作为近似值,都有
X
A
a
b
0
y
右图,我们也可以采用分割、近似代替、求和、取极限的方法,求出A面积.
趁热打铁
你会吗?
X
A
a
b
0
y
A区域的两边分别是A1和A2图中两连续不断的曲线围成.
1
A2
面积 A=A1-A2
思路点击
b
a
1
a
b
x
y
o
a
b
x
y
o
用矩形面积近似取代曲边梯形面积.
显然,小矩形越多,矩形总面积越接近曲边梯形面积.
(四个小矩形)
(九个小矩形)
同理:
将“以直代曲”和“逼近”的思想具体化,求曲边梯形的面积的思想方法:
分割
化整为零
求和
积零为整
取极限
精确值——定积分
求近似:以直(不变)代曲(变)
取极限
过每个分点做平行于y轴的直线,把曲边梯形分成n个小曲边梯形
求曲边梯形面积的方法:
把区间[a,b]分成n个小区间 ,长度为
课堂小结
(1)分割
其中
(2)近似代替
(3)求和
(4)取极限
课堂练习
例1
“求曲边梯形的面积”的思想方法有哪些?
开动脑筋想想吧!
例2
利用学的知识定义计算:
例3
将
写成定积分.
定积分:以直代曲,用“均匀”的研究“不均匀”的;用无限的方法研究有限的问题,从局部到整体.
具体实例:曲边梯形的面积、变速直线运动的路程.
1.4 定积分与微积分基本定理
有什么思路吗?
新课导入
中学学习过:三角形,圆形,矩形,平行四边形,梯形等规则图形面积的计算,而计算平面曲线围成的平面“曲边图形”的面积、变速直线运动物体位移、变力做功等问题.
如何解决这些实际问题呢?
能否把求“曲边图形”面积转化为求“直边图形”面积?能否利用匀速直线运动的知识解决变速直线运动的问题?为此,我们需要学习新的数学知识—— .
定积分
a
b
x
y
o
1.4.1 曲边梯形面积与定积分
曲边梯形的面积怎么求?
教学目标
知识与能力
能根据正多边形逼近圆的面积而求出圆面积的过程,概括出求平面曲边梯形面积的基本思想:在每个局部小范围内“以直代曲”和逼近的思想.
过程与方法
(1)根据“以直代曲”和“逼近”的思想将求曲线梯形面积化为四个步骤:分割、近似代替、求和、取极限.
(2)了解定积分概念中蕴涵的最本质的思想.
情感态度与价值观
利用计算平面“曲边图形”的面积,从实际问题引发学生学习定积分知识的欲望.
教学重难点
重点
“以直代曲”和“以不变代变”的思想方法.
难点
“以直代曲”和“以不变代变”的思想方法.
一般地,如果函数 在某个区间 上的图象是一条连续不断的曲线,那么我们就把它称为区间 上的连续函数.例如
知识点!
图中图形可以看成是直线x=0,x=1,y=0和曲线 所围成的曲边梯形?
例题?
思考?
图中的曲边梯形与我们熟悉的“直边图形”的主要区别是什么?能否将求这个曲边梯形面积s的问题转化为求“直边图形”面积的问题?
在过去的学习中,我们曾用正多边形逼近圆的方法,利用正多边形面积求圆的面积.
用这种“以直代曲”的思想启发我们!
发现!
发现!
曲边梯形与“直边图形”的主要区别是,前者有一边是曲线段,而“直边图形”的所有边都是直线段.
是否也能用直边形(比如矩形)逼近曲边梯形的方法求阴影部分面积?
观察下列演示过程,注意当分割加细时,矩形面积和与曲边梯形面积的关系.
对每个小曲边梯形“以直代曲”,即用矩形的面积近似代替小曲边梯形的面积,得到每个小曲边梯形面积的近似值,对这些近似值求和,就得到曲边梯形面积的近似值.
即用化归为计算矩形面积和逼近的思想方法求出曲边梯形的面积.
在区间[0,1]中任意插入n-1个分点:
把[0,1]分成n个小区间[xi-1, xi] (i=n-1)区间长度为 (i=n-1)
分割:
如图,当n很大时,即△x很小时,在区间 上可以认为函数 的值变化很小.
近似代替:
把曲边梯形分成n个小曲边梯形面积记做 .用小矩形的面积 近似地替代 ,即局部小范围内“以直代曲”.
则阴影部分面积
求和:
得到S(曲边梯形)的近似值:
取极限:
当n趋向于无穷大
当n趋向于无穷大,即 趋向于0时, 趋向于S.从而有
在“近似代替”中,如果认为函数 在区间 上的值近似地等于右端点 处的函数值 ,用这种方法能求出S的值吗?若能求出,这个值也是 吗?取任意 处的函数值 作为近似值,情况又怎样?
探究!
可以证明,取 在区间 上任意一点 处的值 作为近似值,都有
X
A
a
b
0
y
右图,我们也可以采用分割、近似代替、求和、取极限的方法,求出A面积.
趁热打铁
你会吗?
X
A
a
b
0
y
A区域的两边分别是A1和A2图中两连续不断的曲线围成.
1
A2
面积 A=A1-A2
思路点击
b
a
1
a
b
x
y
o
a
b
x
y
o
用矩形面积近似取代曲边梯形面积.
显然,小矩形越多,矩形总面积越接近曲边梯形面积.
(四个小矩形)
(九个小矩形)
同理:
将“以直代曲”和“逼近”的思想具体化,求曲边梯形的面积的思想方法:
分割
化整为零
求和
积零为整
取极限
精确值——定积分
求近似:以直(不变)代曲(变)
取极限
过每个分点做平行于y轴的直线,把曲边梯形分成n个小曲边梯形
求曲边梯形面积的方法:
把区间[a,b]分成n个小区间 ,长度为
课堂小结
(1)分割
其中
(2)近似代替
(3)求和
(4)取极限
课堂练习
例1
“求曲边梯形的面积”的思想方法有哪些?
开动脑筋想想吧!
例2
利用学的知识定义计算:
例3
将
写成定积分.
