高中物理人教版选修3-5 第16章 16.2动量守恒定律(一) 上课课件45张PPT
文档属性
| 名称 | 高中物理人教版选修3-5 第16章 16.2动量守恒定律(一) 上课课件45张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 634.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-16 22:36:07 | ||
图片预览










文档简介
(共45张PPT)
导入新课
为什么汽车的玻璃会碎呢?
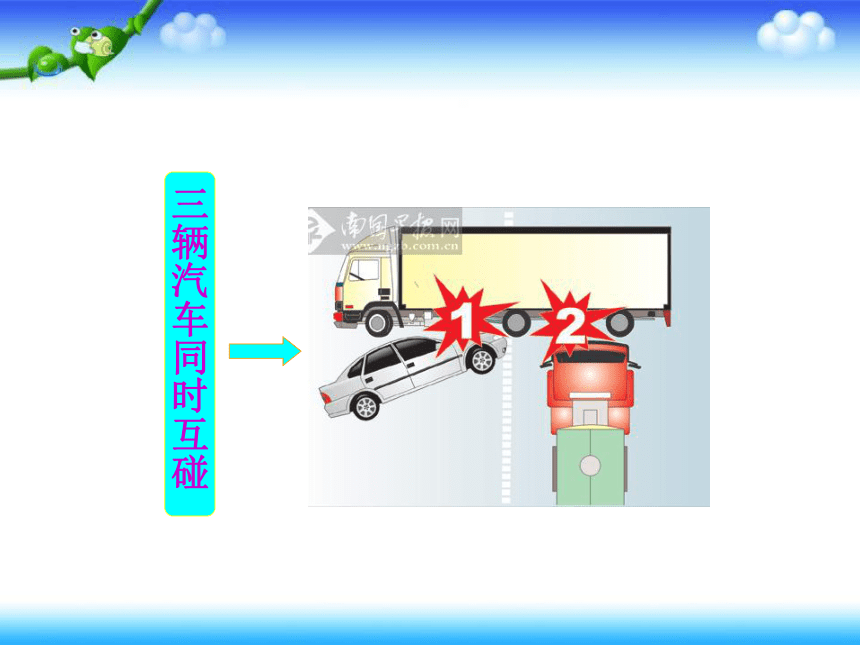
三辆汽车同时互碰
气囊,在发生碰撞时,为您提供四面八方的保护。每个前气囊都带有两级充气装置,可以根据撞击的程度为气囊充气。侧面气囊则可保护前排乘客和躯干部位,而帘式气囊能够挡住车窗,为前后排乘客提供头部的侧面防护。
气囊发生碰撞
第二节动量守恒定律(一)
教学目标
1.知识与技能
理解动量守恒定律的确切含义和表达式。
能用动量定理和牛顿第三定律推导出动量守恒定律。
知道动量守恒定律的适用条件和适用范围。
2. 过程与方法
能结合动量定理和牛顿第三定律推导出动量守恒定律。
学会用动量守恒定律解释现象。
会应用动量守恒定律分析求解一维运动问题。
3. 情感态度与价值观
通过动量守恒定律的推导出,培养学生实事求是的科学态度和严谨的推理方法。
了解自然科学规律发展的深远意义及对社会发展的巨大推动作用。
教学重难点
重点
掌握动量守恒定律的推导、表达式、适用范围和守恒条件。
难点
正确判断系统在所研究的过程中动量是否守恒。
本节导航
1、动量
2、系统 内力和外力
3、动量守恒定律
1、动量
(1)动量定义:
由第一节的知识可以知道物体碰撞前后的质量与速度的乘积不变,把质量与速度的乘积叫动量。
(2)动量的大小:p=mv。
(3)动量的方向:速度的方向是动量的大小。
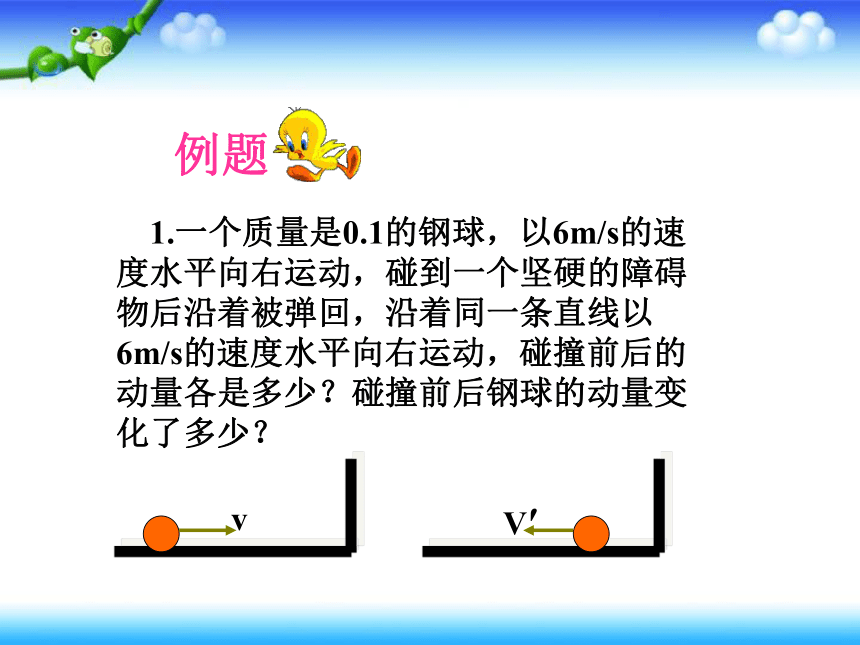
1.一个质量是0.1的钢球,以6m/s的速度水平向右运动,碰到一个坚硬的障碍物后沿着被弹回,沿着同一条直线以6m/s的速度水平向右运动,碰撞前后的动量各是多少?碰撞前后钢球的动量变化了多少?
例题
V′
v
解:取水平向右的方向为坐标轴的方向。碰撞前钢球的速度v=6m/s,碰撞前钢球的动量为
P=mv=0.1×6kgm/s=0.6kgm/s
o
p′
p
△p
x
碰撞后钢球的速度为v′=-6m/s,碰撞后钢球的动量为
p′=m v′=-0.1×6kgm/s=0.6kgm/s
碰撞前后钢球动量的变化为
△p= p′-p=-1.2kgm/s
因为,动量的变化△p是矢量,所以,负号表示动量的方向,与坐标轴的方向相反,方向水平向左。
2、系统 内力和外力
(1)力学系统
碰撞研究的对象不是一个物体,而是两个或是多个物体,而这两个或多个物体就叫做力学系统。
例如:重力势能属于地面附近的物体与地球组成的系统;轻质弹簧产生的弹性势能属于它所连接的两个物体。
(2)内力
碰撞时两个物体之间一定有相互作用力,由于两个物体是属于同一系统,他们之间的力叫做内力。
(3)外力
两个物体之间受到的重力、支持力、摩擦力等一些系统以外施加的力叫做外力。
3、动量守恒定律
(1)动量守恒定律的内容
一个系统不受外力,或者所受外力的矢量和为零,这个系统的总动量把持不变。
(2)动量守恒定律的表达形式
除了 ,即 p1+p2=p1′+p2′。
(3)动量守恒定律成立的条件
①系统不受外力或者所受外力之和为零。
②系统受外力,但外力远小于内力,可以忽略不计。
③系统在某一个方向上所受的合外力为零,则该方向上动量守恒。
④全过程的某一阶段系统受的合外力为零,则该阶段系统动量守恒。
实验
用质量相等的两辆小车,剪断细线,观察它们到达距弹开埏等距离的挡板上时间的先后。问:
①两小车所做的运动,分析小球运动的距离、时间,得到它们的速度有什么关系。
②据动量等于质量与速度的乘积,分析在弹开后各自的动量和总动量各为多大?
①两小车同时被弹开,同时获得加速度,同时到达距弹开处等距离的挡板处,说明在质量相等时两小车被弹出时的速度大小相等、方向相反。
②两小车的动量分别为:mv,-mv,动量的矢量和为0。
结论
例题
2.在列车编组站里,一辆m1为1.8×104kg的货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.2×104kg的静止的货车,它们碰撞后一起继续运动。求货车碰撞后运动的速度。
v
解:沿碰撞前货车运动的速度的方向建立坐标轴如上图,则有v1=2m/s。设两车结合后的速度为v,两车碰转前的总动量为
P=m1v1
碰撞后的总动量为
p′=(m1+m2)v
由动量守恒定律得
m1v1=(m1+m2)v
代入数据得v=0.9m/s
因为两车结合后的速度为正值,所以结合后仍然向后运动。
(4)利用动量定理解题骤:
①明确研究对象和研究过程。
②进行受力分析。
③规定正方向。
④写出研究对象的初、末动量。
⑤根据动量定理列式求解。
课堂小结
(1)动量:
由第一节的知识可以知道物体碰撞前后的质量与速度的乘积不变,把质量与速度的乘积叫动量。
(2)大小:p=mv。
(3)方向:速度的方向是动量的大小。
(4)碰撞中两个或多个物体就叫做力学系统。
(5)两个物体是属于同一系统,他们之间的力叫做内力。
(6)系统以外施加的力叫做外力。
(7)动量守恒定律的内容
一个系统不受外力,或者所受外力的矢量和为零,这个系统的总动量把持不变。(8)动量守恒定律的表达形式
除了 ,即 p1+p2=p1′+p2′。
针对性练习
1.如图所示, A、B 两物体的质量比 mA∶mB=3∶2,它们原来静止在平板车C上,A、B间有一根被压缩了的弹簧,A、B与平板车上表面间的动摩擦因数相同,地面光滑.当弹簧突然释放后,则有( )
A.A、B系统动量守恒
B.A、B、C系统动量守恒
C.小车向左运动
D.小车向右运动
C
A
B
B C
2.动能相同的A、B两球,它们的质量分别为mA、mB,且mA>mB,在光滑的水平面上相向运动,当两球相碰后,其中一球停止运动,则可判定: ( )
A.碰撞前A球的速度小于B球的速度
B.碰撞前A球的动量大于B球的动量
C.碰撞后A球的动量变化大于B球的动量变化
D.碰撞后A球的速度为零,B球朝反方向运动
A B D
3.一个质量为M的雪橇静止在水平雪地上,一条质量为m的爱斯基摩狗站在该雪橇上.狗向雪橇的正后方跳下,随后又追赶并向前跳上雪橇;其后狗又反复地跳下、追赶并跳上雪橇,狗与雪橇始终沿一条直线运动.若狗跳离雪橇时雪橇的速度为V,则此时狗相对于地面的速度为V+u(其中u为狗相对于雪橇的速度,V+u为代数和.若以雪橇运动的方向为正方向,则V为正值,u为负值).设狗总以速度v追赶和跳上雪橇,雪橇与雪地间的摩擦忽略不计.已知v 的大小为5m/s,u的大小为4m/s,M=30kg,m=10kg.
(1)求狗第一次跳上雪橇后两者的共同速度的大小.
(2)求雪橇最终速度的大小和狗最多能跳上雪橇的次数.
(供使用但不一定用到的对数值:lg2=O.301,lg3=0.477)
解:(1)设雪橇运动的方向为正方向,狗第1次跳下雪橇后雪橇的速度为V1,根据动量守恒定律,有
狗第1次跳上雪橇时,雪橇与狗的共同速度 满足
可解得
将
代入,得
(2)解:设雪橇运动的方向为正方向。狗第i 次跳下雪橇后,雪橇的速度为Vi ,狗的速度为Vi+u;狗第i次跳上雪橇后,雪橇和狗的共同速度为 Vi′,由动量守恒定律可得:
第一次跳下雪橇:
MV1+m(V1+u)=0
第一次跳上雪橇:
MV1+mv =(M+m)V1′
第二次跳下雪橇:
第二次跳上雪橇:
MV2+mv =(M+m)V2′
第三次跳下雪橇:
(M+m)V2′= MV3 + m(V3 +u)
第三次跳上雪橇:
(M+m)V3′ = MV3+mv
第四次跳下雪橇:
(M+m)V3 ′= MV4+m(V4+u)
此时雪橇的速度已大于狗追赶的速度,狗将不可能追上雪橇。因此,狗最多能跳上雪橇3次。雪橇最终的速度大小为5.625m/s.
课堂练习
1.如图所示,在高为h=1.25m的光滑平台上,有一质量m2=0.3kg的物体B静止在平台上,另一个质量为m1=0.2kg的物体A以速度v1=5m/s的速度向B运动。A、B碰撞后分离,物体B最后落在平台边离平台右边缘2m处,则物体A应落在平台的 侧,离平台边缘的水平距离为 m。(取g=10m/s2)
左
0.5
v1
A
B
2.AB两球在光滑水平上沿同一直线,同一方向运动,A球的动量5kg.m/s,B球的动量是7kg.m/s,当A球追上B球时发生碰撞,则碰撞后A,B两球的动量可能是( )
A.pA=6kg.m/s pB=6kg.m/s
B.pA=3kg.m/s pB=9kg.m/s
C.pA=-2kg.m/s pB=14kg.m/s
D.pA=-5kg.m/s pB=15kg.m/s
vA
vB
A
B
BC
3.在光滑水平面上,两球沿球心连线以相等速率相向而行,下列现象可能的是( )
A.若两球质量相等,碰后以某一相等速率互相分开.
B.若两球质量相等,碰后以某一相等速率同向而行.
C.若两球质量不同,碰后以某一相等速率互相分开.
D.若两球质量不同,碰后以某一相等速率同向而行.
AD
4.如图所示,小球A以速率v0向右运动时跟静止的小球B发生碰撞,碰后A球以 V0/2 的速率弹回,而B球以V0/3 的速率向右运动,求A、B两球的质量之比。
v0
A
B
答案: 2:9
5.质量为10g的小球甲在光滑的水平桌面上以30cm/s的速率向右运动,恰遇上质量为50g的小球乙以10cm/s的速率向左运动,碰撞后,小球乙恰好静止。那么,碰撞后小球甲的速度多大?方向如何?
A
B
C
20cm/s 方向向左
(3)取向东为正方向,则B物体的速度为vB=-4m/s,两物体动量之和为-6kgm/s.动量之和为33J
小结:动量是适量,单位是kgm/s;动量是标量,单位是焦耳。运算法则不同,动量遵循矢量的平行四边形法则,动量遵循代数加减法则。
2.解:因为在光滑水平面上的摩擦力可以忽略,因此可以认为甲乙两同学组成的系统所受外力的矢量和为零,满足动量守恒的条件。所以,甲推乙后,他们的总动量仍为零,甲乙两人各自的动量的大小相等,方向相反,矢量和为零。
设甲乙的速度为v甲和v乙,取甲的方向为正方向,根据动量守恒定律有
0=m甲v甲+m乙(-v乙)
由此解出 v甲/v乙=m乙/m甲=0.9
3.解:由于在A、B运动的过程中,除了两者之间的相互作用力,其它的力可以忽略,即A、B组成的系统所受外力的矢量和为零,满足动量守恒定律的条件。取初速度方向为正方向,根据动量守恒定律,有
mAVA=+mBvB=mAvA′+mBvB′
由此解出vA′=7.4m/s
A的速度大小为7.4m/s,方向与初速度方向相同。
4.解:因为木块在光滑水平桌面上,所受的摩擦力为零,且子弹与木块的相互作用属于系统的内力,因此整个系统所受外力的适量和为零,满足动量守恒定律的条件。
取子弹的初速度方向为正方向。
若子弹留在木块中,一直子弹的质量为0.01kg,初速度为300m/s,木块的质量为0.024kg,初速度为零,根据动量守恒定律,有v=88.2m/s.若子弹穿过木块后,子弹的速度为v2′=88.3m/s.
导入新课
为什么汽车的玻璃会碎呢?
三辆汽车同时互碰
气囊,在发生碰撞时,为您提供四面八方的保护。每个前气囊都带有两级充气装置,可以根据撞击的程度为气囊充气。侧面气囊则可保护前排乘客和躯干部位,而帘式气囊能够挡住车窗,为前后排乘客提供头部的侧面防护。
气囊发生碰撞
第二节动量守恒定律(一)
教学目标
1.知识与技能
理解动量守恒定律的确切含义和表达式。
能用动量定理和牛顿第三定律推导出动量守恒定律。
知道动量守恒定律的适用条件和适用范围。
2. 过程与方法
能结合动量定理和牛顿第三定律推导出动量守恒定律。
学会用动量守恒定律解释现象。
会应用动量守恒定律分析求解一维运动问题。
3. 情感态度与价值观
通过动量守恒定律的推导出,培养学生实事求是的科学态度和严谨的推理方法。
了解自然科学规律发展的深远意义及对社会发展的巨大推动作用。
教学重难点
重点
掌握动量守恒定律的推导、表达式、适用范围和守恒条件。
难点
正确判断系统在所研究的过程中动量是否守恒。
本节导航
1、动量
2、系统 内力和外力
3、动量守恒定律
1、动量
(1)动量定义:
由第一节的知识可以知道物体碰撞前后的质量与速度的乘积不变,把质量与速度的乘积叫动量。
(2)动量的大小:p=mv。
(3)动量的方向:速度的方向是动量的大小。
1.一个质量是0.1的钢球,以6m/s的速度水平向右运动,碰到一个坚硬的障碍物后沿着被弹回,沿着同一条直线以6m/s的速度水平向右运动,碰撞前后的动量各是多少?碰撞前后钢球的动量变化了多少?
例题
V′
v
解:取水平向右的方向为坐标轴的方向。碰撞前钢球的速度v=6m/s,碰撞前钢球的动量为
P=mv=0.1×6kgm/s=0.6kgm/s
o
p′
p
△p
x
碰撞后钢球的速度为v′=-6m/s,碰撞后钢球的动量为
p′=m v′=-0.1×6kgm/s=0.6kgm/s
碰撞前后钢球动量的变化为
△p= p′-p=-1.2kgm/s
因为,动量的变化△p是矢量,所以,负号表示动量的方向,与坐标轴的方向相反,方向水平向左。
2、系统 内力和外力
(1)力学系统
碰撞研究的对象不是一个物体,而是两个或是多个物体,而这两个或多个物体就叫做力学系统。
例如:重力势能属于地面附近的物体与地球组成的系统;轻质弹簧产生的弹性势能属于它所连接的两个物体。
(2)内力
碰撞时两个物体之间一定有相互作用力,由于两个物体是属于同一系统,他们之间的力叫做内力。
(3)外力
两个物体之间受到的重力、支持力、摩擦力等一些系统以外施加的力叫做外力。
3、动量守恒定律
(1)动量守恒定律的内容
一个系统不受外力,或者所受外力的矢量和为零,这个系统的总动量把持不变。
(2)动量守恒定律的表达形式
除了 ,即 p1+p2=p1′+p2′。
(3)动量守恒定律成立的条件
①系统不受外力或者所受外力之和为零。
②系统受外力,但外力远小于内力,可以忽略不计。
③系统在某一个方向上所受的合外力为零,则该方向上动量守恒。
④全过程的某一阶段系统受的合外力为零,则该阶段系统动量守恒。
实验
用质量相等的两辆小车,剪断细线,观察它们到达距弹开埏等距离的挡板上时间的先后。问:
①两小车所做的运动,分析小球运动的距离、时间,得到它们的速度有什么关系。
②据动量等于质量与速度的乘积,分析在弹开后各自的动量和总动量各为多大?
①两小车同时被弹开,同时获得加速度,同时到达距弹开处等距离的挡板处,说明在质量相等时两小车被弹出时的速度大小相等、方向相反。
②两小车的动量分别为:mv,-mv,动量的矢量和为0。
结论
例题
2.在列车编组站里,一辆m1为1.8×104kg的货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.2×104kg的静止的货车,它们碰撞后一起继续运动。求货车碰撞后运动的速度。
v
解:沿碰撞前货车运动的速度的方向建立坐标轴如上图,则有v1=2m/s。设两车结合后的速度为v,两车碰转前的总动量为
P=m1v1
碰撞后的总动量为
p′=(m1+m2)v
由动量守恒定律得
m1v1=(m1+m2)v
代入数据得v=0.9m/s
因为两车结合后的速度为正值,所以结合后仍然向后运动。
(4)利用动量定理解题骤:
①明确研究对象和研究过程。
②进行受力分析。
③规定正方向。
④写出研究对象的初、末动量。
⑤根据动量定理列式求解。
课堂小结
(1)动量:
由第一节的知识可以知道物体碰撞前后的质量与速度的乘积不变,把质量与速度的乘积叫动量。
(2)大小:p=mv。
(3)方向:速度的方向是动量的大小。
(4)碰撞中两个或多个物体就叫做力学系统。
(5)两个物体是属于同一系统,他们之间的力叫做内力。
(6)系统以外施加的力叫做外力。
(7)动量守恒定律的内容
一个系统不受外力,或者所受外力的矢量和为零,这个系统的总动量把持不变。(8)动量守恒定律的表达形式
除了 ,即 p1+p2=p1′+p2′。
针对性练习
1.如图所示, A、B 两物体的质量比 mA∶mB=3∶2,它们原来静止在平板车C上,A、B间有一根被压缩了的弹簧,A、B与平板车上表面间的动摩擦因数相同,地面光滑.当弹簧突然释放后,则有( )
A.A、B系统动量守恒
B.A、B、C系统动量守恒
C.小车向左运动
D.小车向右运动
C
A
B
B C
2.动能相同的A、B两球,它们的质量分别为mA、mB,且mA>mB,在光滑的水平面上相向运动,当两球相碰后,其中一球停止运动,则可判定: ( )
A.碰撞前A球的速度小于B球的速度
B.碰撞前A球的动量大于B球的动量
C.碰撞后A球的动量变化大于B球的动量变化
D.碰撞后A球的速度为零,B球朝反方向运动
A B D
3.一个质量为M的雪橇静止在水平雪地上,一条质量为m的爱斯基摩狗站在该雪橇上.狗向雪橇的正后方跳下,随后又追赶并向前跳上雪橇;其后狗又反复地跳下、追赶并跳上雪橇,狗与雪橇始终沿一条直线运动.若狗跳离雪橇时雪橇的速度为V,则此时狗相对于地面的速度为V+u(其中u为狗相对于雪橇的速度,V+u为代数和.若以雪橇运动的方向为正方向,则V为正值,u为负值).设狗总以速度v追赶和跳上雪橇,雪橇与雪地间的摩擦忽略不计.已知v 的大小为5m/s,u的大小为4m/s,M=30kg,m=10kg.
(1)求狗第一次跳上雪橇后两者的共同速度的大小.
(2)求雪橇最终速度的大小和狗最多能跳上雪橇的次数.
(供使用但不一定用到的对数值:lg2=O.301,lg3=0.477)
解:(1)设雪橇运动的方向为正方向,狗第1次跳下雪橇后雪橇的速度为V1,根据动量守恒定律,有
狗第1次跳上雪橇时,雪橇与狗的共同速度 满足
可解得
将
代入,得
(2)解:设雪橇运动的方向为正方向。狗第i 次跳下雪橇后,雪橇的速度为Vi ,狗的速度为Vi+u;狗第i次跳上雪橇后,雪橇和狗的共同速度为 Vi′,由动量守恒定律可得:
第一次跳下雪橇:
MV1+m(V1+u)=0
第一次跳上雪橇:
MV1+mv =(M+m)V1′
第二次跳下雪橇:
第二次跳上雪橇:
MV2+mv =(M+m)V2′
第三次跳下雪橇:
(M+m)V2′= MV3 + m(V3 +u)
第三次跳上雪橇:
(M+m)V3′ = MV3+mv
第四次跳下雪橇:
(M+m)V3 ′= MV4+m(V4+u)
此时雪橇的速度已大于狗追赶的速度,狗将不可能追上雪橇。因此,狗最多能跳上雪橇3次。雪橇最终的速度大小为5.625m/s.
课堂练习
1.如图所示,在高为h=1.25m的光滑平台上,有一质量m2=0.3kg的物体B静止在平台上,另一个质量为m1=0.2kg的物体A以速度v1=5m/s的速度向B运动。A、B碰撞后分离,物体B最后落在平台边离平台右边缘2m处,则物体A应落在平台的 侧,离平台边缘的水平距离为 m。(取g=10m/s2)
左
0.5
v1
A
B
2.AB两球在光滑水平上沿同一直线,同一方向运动,A球的动量5kg.m/s,B球的动量是7kg.m/s,当A球追上B球时发生碰撞,则碰撞后A,B两球的动量可能是( )
A.pA=6kg.m/s pB=6kg.m/s
B.pA=3kg.m/s pB=9kg.m/s
C.pA=-2kg.m/s pB=14kg.m/s
D.pA=-5kg.m/s pB=15kg.m/s
vA
vB
A
B
BC
3.在光滑水平面上,两球沿球心连线以相等速率相向而行,下列现象可能的是( )
A.若两球质量相等,碰后以某一相等速率互相分开.
B.若两球质量相等,碰后以某一相等速率同向而行.
C.若两球质量不同,碰后以某一相等速率互相分开.
D.若两球质量不同,碰后以某一相等速率同向而行.
AD
4.如图所示,小球A以速率v0向右运动时跟静止的小球B发生碰撞,碰后A球以 V0/2 的速率弹回,而B球以V0/3 的速率向右运动,求A、B两球的质量之比。
v0
A
B
答案: 2:9
5.质量为10g的小球甲在光滑的水平桌面上以30cm/s的速率向右运动,恰遇上质量为50g的小球乙以10cm/s的速率向左运动,碰撞后,小球乙恰好静止。那么,碰撞后小球甲的速度多大?方向如何?
A
B
C
20cm/s 方向向左
(3)取向东为正方向,则B物体的速度为vB=-4m/s,两物体动量之和为-6kgm/s.动量之和为33J
小结:动量是适量,单位是kgm/s;动量是标量,单位是焦耳。运算法则不同,动量遵循矢量的平行四边形法则,动量遵循代数加减法则。
2.解:因为在光滑水平面上的摩擦力可以忽略,因此可以认为甲乙两同学组成的系统所受外力的矢量和为零,满足动量守恒的条件。所以,甲推乙后,他们的总动量仍为零,甲乙两人各自的动量的大小相等,方向相反,矢量和为零。
设甲乙的速度为v甲和v乙,取甲的方向为正方向,根据动量守恒定律有
0=m甲v甲+m乙(-v乙)
由此解出 v甲/v乙=m乙/m甲=0.9
3.解:由于在A、B运动的过程中,除了两者之间的相互作用力,其它的力可以忽略,即A、B组成的系统所受外力的矢量和为零,满足动量守恒定律的条件。取初速度方向为正方向,根据动量守恒定律,有
mAVA=+mBvB=mAvA′+mBvB′
由此解出vA′=7.4m/s
A的速度大小为7.4m/s,方向与初速度方向相同。
4.解:因为木块在光滑水平桌面上,所受的摩擦力为零,且子弹与木块的相互作用属于系统的内力,因此整个系统所受外力的适量和为零,满足动量守恒定律的条件。
取子弹的初速度方向为正方向。
若子弹留在木块中,一直子弹的质量为0.01kg,初速度为300m/s,木块的质量为0.024kg,初速度为零,根据动量守恒定律,有v=88.2m/s.若子弹穿过木块后,子弹的速度为v2′=88.3m/s.
