北师大版八年级数学下册1.2直角三角形同步测试含答案
文档属性
| 名称 | 北师大版八年级数学下册1.2直角三角形同步测试含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 131.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 08:32:25 | ||
图片预览

文档简介
1.2直角三角形同步测试
1、选择题
1.如果两个直角三角形的两条直角边对应相等,那么两个直角三角形全等的
依据是( )
? A. AAS? B.SAS? C.HL? D.SSS
2.直角三角形的两条直角边分别12cm和16cm,斜边为20cm,则斜边上的高为( )
A. 10cm B.? 8cm C.? 9.6cm D.9.1cm
3. 如图,AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形( )
? A.5对; B.4对; C.3对; D.2对
4.下列结论错误的是( )
A.全等三角形对应边上的高相等
B.全等三角形对应边上的中线相等
C.两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等
D.两个直角三角形中,两个锐角相等,则这两个三角形全等
5.直角三角形的一个锐角是23°,则另一个锐角等于( )
A.23° B.53° C.57° D.67°
6.. 两个直角三角形全等的条件是( )
A.一锐角对应相等?; B.两锐角对应相等;
C.一条边对应相等; ?D.两条边对应相等
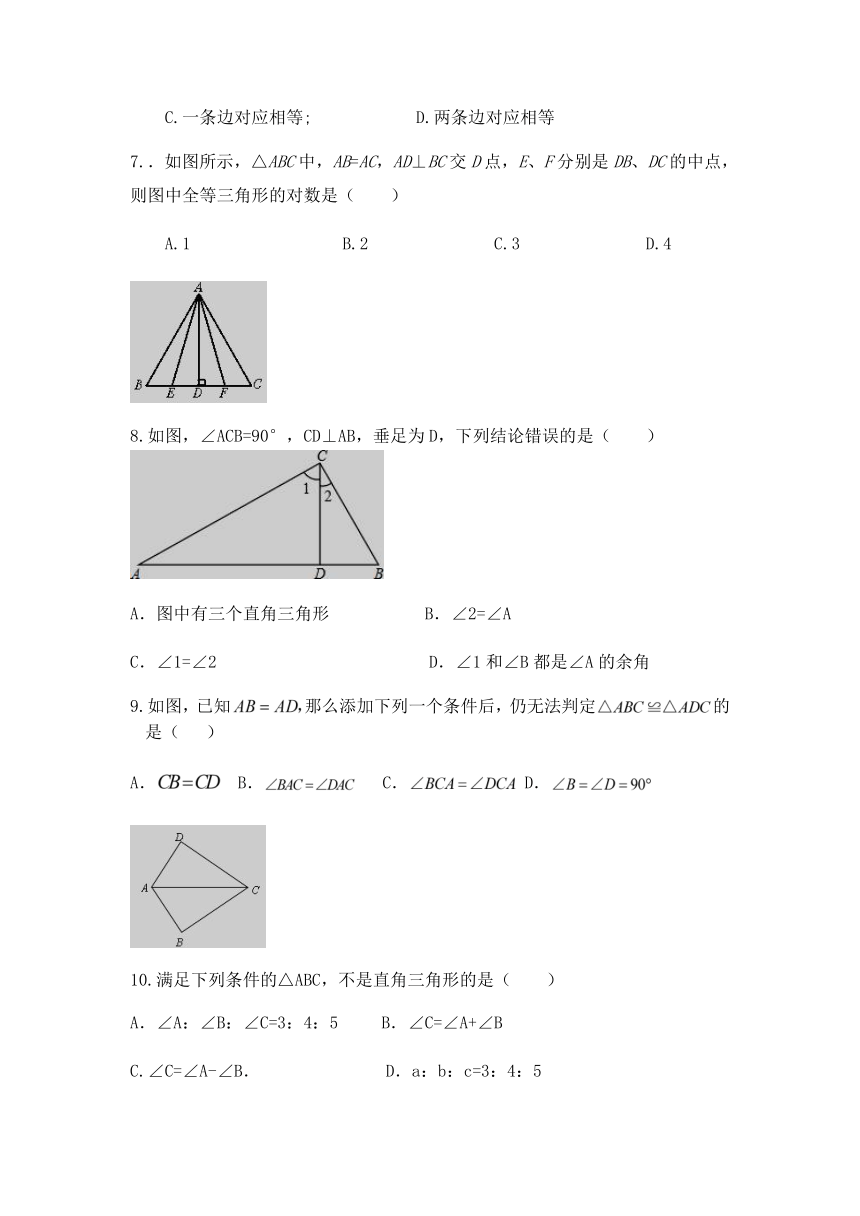
7..如图所示,△ABC中,AB=AC,AD⊥BC交D点,E、F分别是DB、DC的中点,则图中全等三角形的对数是( )
A.1 B.2 C.3 D.4
8.如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( )
A.图中有三个直角三角形 B.∠2=∠A
C.∠1=∠2 D.∠1和∠B都是∠A的余角
9.如图,已知那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
10.满足下列条件的△ABC,不是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.∠C=∠A+∠B
C.∠C=∠A-∠B. D.a:b:c=3:4:5
2、填空题
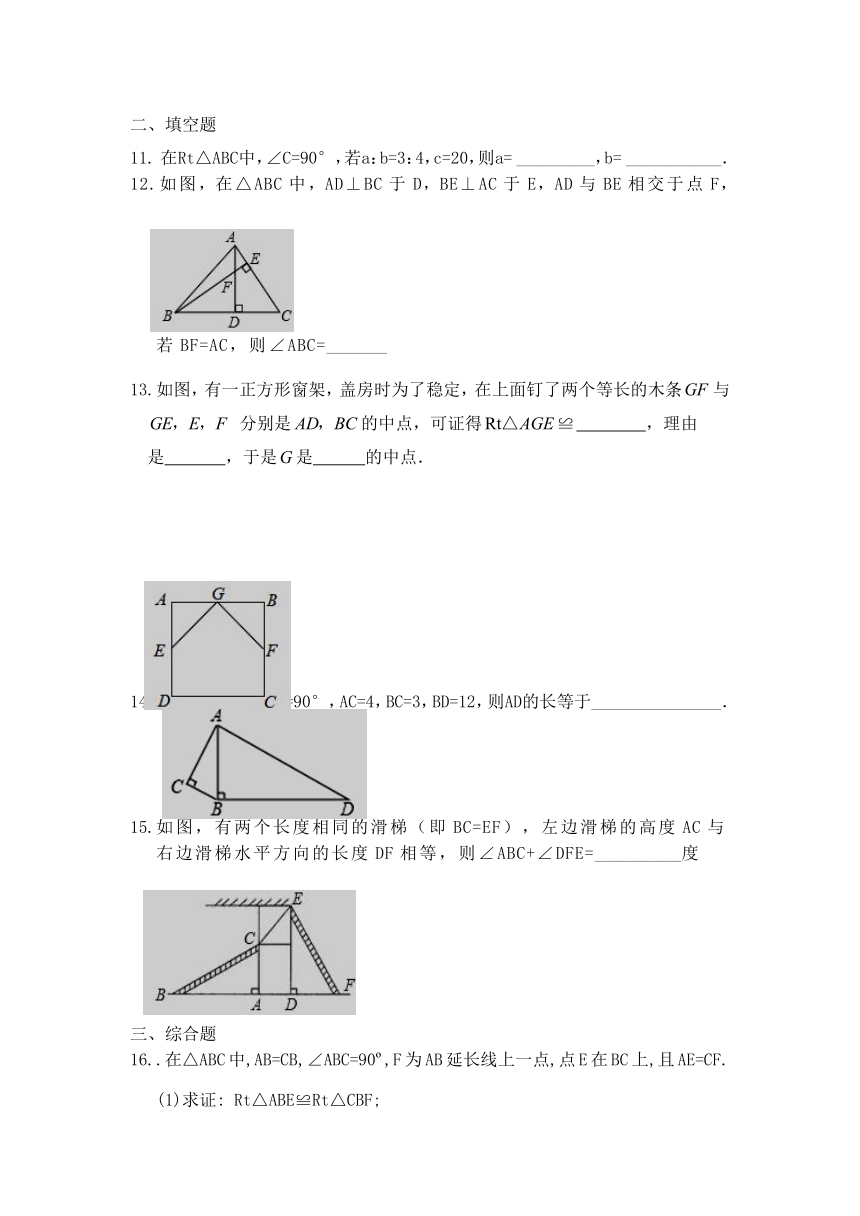
11. 在Rt△ABC中,∠C=90°,若a:b=3:4,c=20,则a= _________,b= ___________.
12.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC=_______
13.如图,有一正方形窗架,盖房时为了稳定,在上面钉了两个等长的木条与 分别是的中点,可证得 ,理由是 ,于是是 的中点.
14. 如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,则AD的长等于_______________.
15.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=__________度
3、综合题
16..在△ABC中,AB=CB,∠ABC=90?,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证: Rt△ABE≌Rt△CBF;
(2)若∠CAE=30?,求∠ACF度数.
17.如图,已知分别是两个钝角和的高,如果,.
求证:.
18.已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
19.已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.
(1)求证: AF=CE.
(2)求证:AB∥CD.
1.2直角三角形同步测试答案
1、选择题
1.B 2.C 3.C 4.D 5.D 6.D 7.D 8.A 9.C 10.A
二、填空题
11. 12 16
12.45°
13.,HL,
14.13
三、综合题
16.解:(1)∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∵AE=CF, AB=BC,
∴Rt△ABE≌Rt△CBF(HL)
(2) ∵AB=BC, ∠ABC=90°,
∴ ∠CAB=∠ACB=45°.
∵∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知 Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠ACB=45°+15°=60°.
17. 解:根据“”证,
,再根据“”证,
,,即.
18.证明:∵BD⊥AE于D,CE⊥AE于E
?∴∠ADB=∠AEC=90°
?∵∠BAC=90°
?∴∠ABD+∠BAD=∠CAE+∠BAD
?∴∠ABD=∠CAE
?在△ABD和△CAE中
?∴△ABD≌△CAE(AAS)
?∴BD=AE,AD=CE
?∵AE=AD+DE
?∴BD=CE+DE
19.证明:(1)∵DE⊥AC,BF⊥AC,
∴在Rt△DCE和Rt△BAF中,
AB=CD,DE=BF,
∴Rt△DCE≌Rt△BAF(HL),
∴AF=CE;
(2)由(1)中Rt△DCE≌Rt△BAF,
可得∠C=∠A,
∴AB∥CD.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
