高中数学人教B版必修3 第三章 3.2.2概率的一般加法公式(选)上课课件(共37张PPT)
文档属性
| 名称 | 高中数学人教B版必修3 第三章 3.2.2概率的一般加法公式(选)上课课件(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 509.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-19 19:50:29 | ||
图片预览









文档简介
(共37张PPT)
新课导入
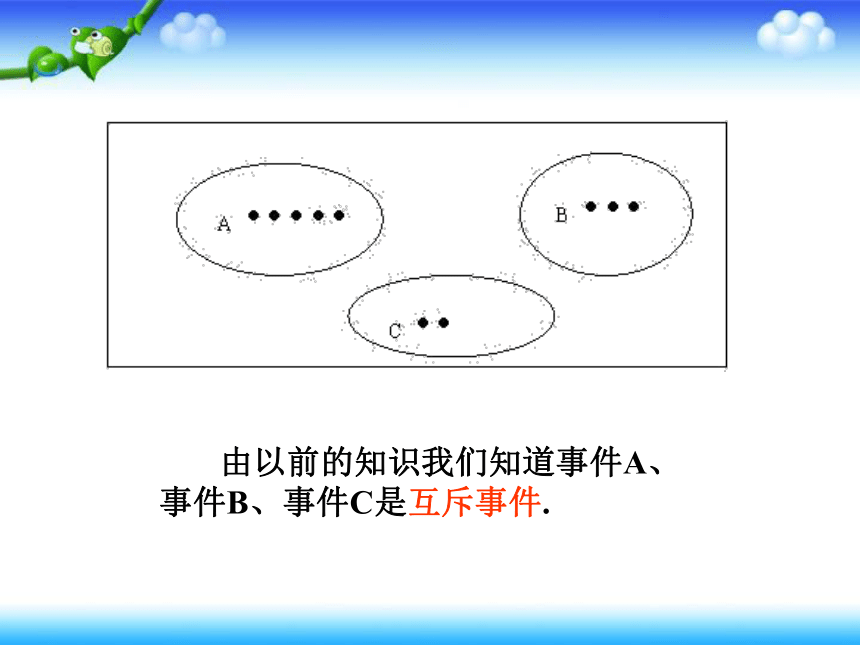
1个盒内放有10个大小相同的乒乓球,其中5个红球,3个绿球,2个黄球,若从中任取一个球,得到红球记为“事件A”,从中任取一个球,得到绿球记为“事件B”,从中任取一个球,得到黄球记为“事件C”,则事件A、B、C之间存在什么关系?
案例1
由以前的知识我们知道事件A、事件B、事件C是互斥事件.
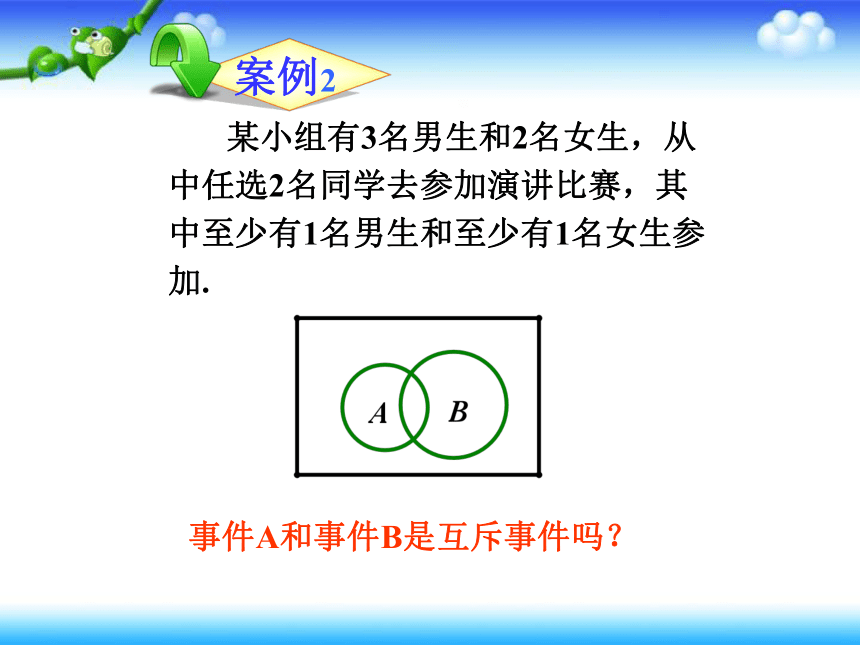
某小组有3名男生和2名女生,从中任选2名同学去参加演讲比赛,其中至少有1名男生和至少有1名女生参加.
事件A和事件B是互斥事件吗?
案例2
3.2.2 概率的一般加法公式
使学生正确理解“互斥事件”,“彼此互斥”和“对立事件”的概念,理解并掌握当A,B互斥时和不是互斥时“事件AUB”的含义,回忆两个互斥事件的概率加法公式,掌握两个不是互斥事件的概率加法公式,同时,会应用所学知识解决一些简单的实际问题.
教学目标
知识与能力
在本节教学中,通过日常生活中的大量实例,鼓励学生动手试验,引导学生学会如何观察、推理、归纳、类比、引申、反思和评价,注重培养学生的数学交流表达的能力,知识间纵横迁移的视角转换能力,提高直觉思维能力.
过程与方法
增强学生合作学习交流的机会,感受与他人合作的重要性,同时养成手、口、眼、耳、脑五官并用的良好习惯.
情感态度与价值观
本节的教学重点是当两个事件不是互斥事件时概率的加法公式.
教学重难点
重点
教学难点是非互斥事件与对立事件加法公式的推导.
难点
知识回顾
1.互斥事件:不可能同时发生的两个事件叫做互斥事件(或称为互不相容事件);
一般地,如果事件A1、 A2、…, An任何两个都是互斥事件,那么就说事件A1、 A2、…, An彼此互斥.
从集合的观点看,几个事件彼此互斥,是指由各个事件的结果组成的集合彼此互不相交.
2.对立事件:不能同时发生且必有一个发生的两个事件叫做互为对立事件.
3.事件的并:由事件A和B至少有一个发生(即A发生,或B发生,或A、B都发生)所构成的事件C,称为事件A与B的并(或和).记作C=A∪B(或C=A+B).
事件A∪B是由事件A或B所包含的基本事件所组成的集合.
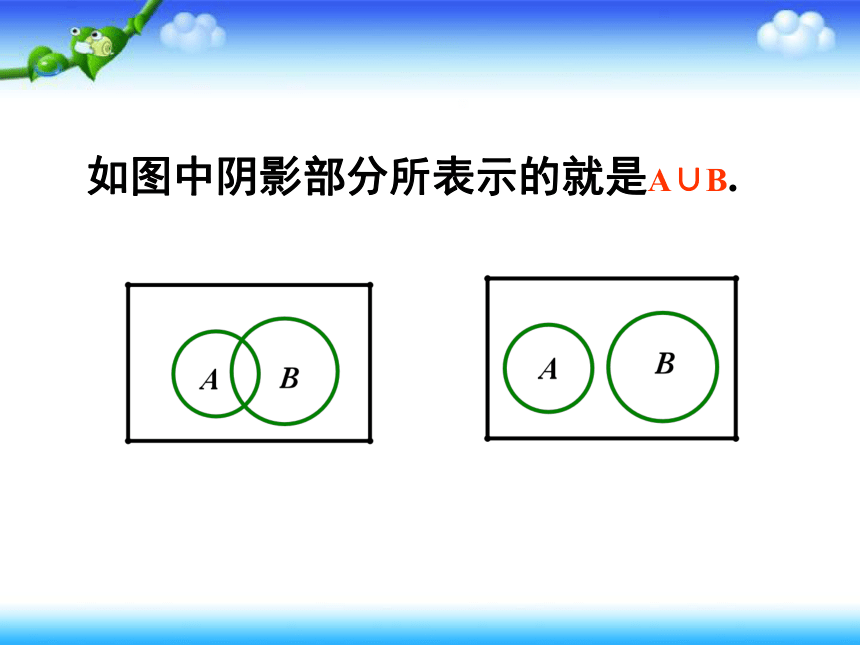
如图中阴影部分所表示的就是A∪B.
如果事件A、B互斥,那么事件A ∪ B发生(即A、B中至少有一个发生)的概率,等于事件A、B分别发生的概率的和.
结论
[推广]一般地,如果事件A1,A2,…,An彼此互斥,那么事件A1 ∪ A2 ∪ … ∪ An(即A1,A2,…,An有一个发生)的概率,等于这n个事件发生的概率的和,即
P( A1 ∪ A2 ∪ … ∪ An)=P(A1)+P(A2)+…+P(An)
那么如果两个事件不互斥呢?
公式是否成立呢?我们看下面的例子.
思考
例1 掷红、蓝两颗骰子.事件A={红骰子点数大于3},事件B={蓝骰子的点数大于3},求事件A∪B={至少有一颗骰子点数大于3}发生的概率.
例题
分析:显然,事件A与B不是互斥的.例如,蓝骰子出现4点时,红骰子也可能出现4点.我们把由事件A和B同时发生所构成的事件D,称为事件A与B的交(或积),记作D=A∩B(或D=AB).
事件A∩B是由事件A和B所共同含有的基本事件组成的集合.如图所示中阴影部分就是表示A∩B.
A
B
本例中,A∩B为{(4,4), (4,5), (4,6), (5,4), (5,5), (5,6), (6,4), (6,5), (6,6)},其中小括号内的左、右两个数分别表示红、蓝骰子出现的点数.
解:做点集Ω={(x,y)
|x∈N,y∈N,1≤x≤6, 1≤y≤6}.
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
在点的坐标(x,y)中,x表示红骰子出现的点数,y表示蓝骰子出现的点数,则Ω就表示试验可能出现的结果的全体构成的集合.因为
Ω中元素的总个数=6×6=36,
A中元素的个数=18,
B中元素的个数=18,
A∪B中元素的个数=27,
所以P( A∪B)=?.
在本例中,因为A∩B≠
所以P( A∪B)≠P(A)+ P(B).
我们在古典概型的情况下推导概率的一般加法公式.
探究
设A,B是Ω的两个事件.如图,容易看出,
A∩B中基本事件的个数等于A中基本事件的个数.
A
B
P( A∪B)=
=
=P(A)+P(B)- (A∩B)
即P(A∪B)=P(A)+P(B)- (A∩B)
结论
例2一个电路板上装有甲、乙两根熔丝,甲熔断的概率为0.85,乙熔断的概率为0.74,两根同时熔断的概率为0.63,求至少有一根熔断的概率.
解析:设 “甲熔丝熔断”, “乙熔丝熔断”,则“甲、乙两根熔丝中至少有一根熔断”为事件 .
所以P(A∪B)=P(A)+P(B)- (A∩B)= 0.85+0.74-0.63=0.96.
我们知道,事件的关系、运算与集合的关系、运算十分类似,在它们之间可以建立一个对应关系.因此,可以从集合的观点来看待事件.比如不可能事件对应于空集 ;必然事件对应于全集 ;事件 与 之并对应于两个集合的并 ;事件与 之交对应于两个集合的交等.
这样,类比集合中的容斥原理:
Card( A∪B )= Card (A)+ Card (B)- Card (A∩B)
可以得到概率加法公式的一般形式:
P(A∪B)=P(A)+P(B)- (A∩B) .
特别地,若事件 与 是互斥事件,则 是不可能事件,有 P(A∩B)=0 ,这时P(A∪B)=P(A)+P(B) ,即是互斥事件的概率加法公式.
课堂小结
3.当两个事件不互斥时,推论:P(A+B+C)=P(A)+P (B) +P (C)-
P(AB)- P(AC)- P(BC)+ P(ABC)
1.当两个事件互斥时
P(A+B)= P(A)+ P(B)
2.当两个事件不互斥时
P(A+B)= P(A)+ P(B)-P(AB)
思想和方法总结
做题先要判断两个事件是否是互斥事件,如果是互斥
P(A+B)= P(A)+ P(B)
如果不互斥
P(A+B)= P(A)+ P(B)-P(AB)
课堂练习
1.射手甲一次击中目标的概率为0.7,射手乙一次击中目标的概率为0.5,现在甲、乙两人同时向一个目标射击一次,则目标被击中概率是 .甲、乙都击不中目标的概率是 .
0.05
0 .95
2.打靶时甲每打10次可击中8次,乙每打10次可击中7次,若两人同时射击一个目标,他们都中靶的概率是 .
14/25
3. 甲、乙两门高射炮同时向一敌机开炮,已知甲击中敌机的概率为0.6,乙击中敌机的概率为0.8,甲、乙同时击中敌机的概率为0.48,求敌机被击中的概率.
解析:设 “甲击中敌机”, “乙击中敌机”,则“两人至少有一人击中敌机”为事件 .
所以 P(A∪B)=P(A)+P(B)- (A∩B)= 0.6+0.6-0.36=0.84.
故两人都击不中为 1- P(A∪B)=1-0.84=0.16.
4.某储蓄卡的密码是1中4位数字号码,每位上的数字可以在0,1,2,……9这10个数字中选取
⑴使用该储蓄卡时随意按下1个4位数字,正好按对密码的概率是多少?
⑵某人未记准储蓄卡密码的最后一位,如果他在使用时随意按下一个数字,正好按对的概率是多少?
(1)1/10000,(2)10/1.
5.如图,在一段电路中并联着3个电池作为电源,如果其中1个或2个损环电路仍能正常工作,已知电池A,B,C损坏的概率均为0.7,求电路正常工作的概率,并分析为什么选择并联电路?
A
B
C
解析:P=1-(1-0.7)(1-0.7)(1-0.7)=0.973;由于并联电路的稳定性,除非3个电池全部损坏,否则电路仍然能正常工作.
甲、乙、丙三名同学,在数学课后独立完成6道同步练习题,甲及格的概率为0.8,乙及格的概率为0.6,丙及格的概率为0.7,则现在三人各答一道题,则三人中只有一人及格的概率为 .
47/250
针对性练习
新课导入
1个盒内放有10个大小相同的乒乓球,其中5个红球,3个绿球,2个黄球,若从中任取一个球,得到红球记为“事件A”,从中任取一个球,得到绿球记为“事件B”,从中任取一个球,得到黄球记为“事件C”,则事件A、B、C之间存在什么关系?
案例1
由以前的知识我们知道事件A、事件B、事件C是互斥事件.
某小组有3名男生和2名女生,从中任选2名同学去参加演讲比赛,其中至少有1名男生和至少有1名女生参加.
事件A和事件B是互斥事件吗?
案例2
3.2.2 概率的一般加法公式
使学生正确理解“互斥事件”,“彼此互斥”和“对立事件”的概念,理解并掌握当A,B互斥时和不是互斥时“事件AUB”的含义,回忆两个互斥事件的概率加法公式,掌握两个不是互斥事件的概率加法公式,同时,会应用所学知识解决一些简单的实际问题.
教学目标
知识与能力
在本节教学中,通过日常生活中的大量实例,鼓励学生动手试验,引导学生学会如何观察、推理、归纳、类比、引申、反思和评价,注重培养学生的数学交流表达的能力,知识间纵横迁移的视角转换能力,提高直觉思维能力.
过程与方法
增强学生合作学习交流的机会,感受与他人合作的重要性,同时养成手、口、眼、耳、脑五官并用的良好习惯.
情感态度与价值观
本节的教学重点是当两个事件不是互斥事件时概率的加法公式.
教学重难点
重点
教学难点是非互斥事件与对立事件加法公式的推导.
难点
知识回顾
1.互斥事件:不可能同时发生的两个事件叫做互斥事件(或称为互不相容事件);
一般地,如果事件A1、 A2、…, An任何两个都是互斥事件,那么就说事件A1、 A2、…, An彼此互斥.
从集合的观点看,几个事件彼此互斥,是指由各个事件的结果组成的集合彼此互不相交.
2.对立事件:不能同时发生且必有一个发生的两个事件叫做互为对立事件.
3.事件的并:由事件A和B至少有一个发生(即A发生,或B发生,或A、B都发生)所构成的事件C,称为事件A与B的并(或和).记作C=A∪B(或C=A+B).
事件A∪B是由事件A或B所包含的基本事件所组成的集合.
如图中阴影部分所表示的就是A∪B.
如果事件A、B互斥,那么事件A ∪ B发生(即A、B中至少有一个发生)的概率,等于事件A、B分别发生的概率的和.
结论
[推广]一般地,如果事件A1,A2,…,An彼此互斥,那么事件A1 ∪ A2 ∪ … ∪ An(即A1,A2,…,An有一个发生)的概率,等于这n个事件发生的概率的和,即
P( A1 ∪ A2 ∪ … ∪ An)=P(A1)+P(A2)+…+P(An)
那么如果两个事件不互斥呢?
公式是否成立呢?我们看下面的例子.
思考
例1 掷红、蓝两颗骰子.事件A={红骰子点数大于3},事件B={蓝骰子的点数大于3},求事件A∪B={至少有一颗骰子点数大于3}发生的概率.
例题
分析:显然,事件A与B不是互斥的.例如,蓝骰子出现4点时,红骰子也可能出现4点.我们把由事件A和B同时发生所构成的事件D,称为事件A与B的交(或积),记作D=A∩B(或D=AB).
事件A∩B是由事件A和B所共同含有的基本事件组成的集合.如图所示中阴影部分就是表示A∩B.
A
B
本例中,A∩B为{(4,4), (4,5), (4,6), (5,4), (5,5), (5,6), (6,4), (6,5), (6,6)},其中小括号内的左、右两个数分别表示红、蓝骰子出现的点数.
解:做点集Ω={(x,y)
|x∈N,y∈N,1≤x≤6, 1≤y≤6}.
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
在点的坐标(x,y)中,x表示红骰子出现的点数,y表示蓝骰子出现的点数,则Ω就表示试验可能出现的结果的全体构成的集合.因为
Ω中元素的总个数=6×6=36,
A中元素的个数=18,
B中元素的个数=18,
A∪B中元素的个数=27,
所以P( A∪B)=?.
在本例中,因为A∩B≠
所以P( A∪B)≠P(A)+ P(B).
我们在古典概型的情况下推导概率的一般加法公式.
探究
设A,B是Ω的两个事件.如图,容易看出,
A∩B中基本事件的个数等于A中基本事件的个数.
A
B
P( A∪B)=
=
=P(A)+P(B)- (A∩B)
即P(A∪B)=P(A)+P(B)- (A∩B)
结论
例2一个电路板上装有甲、乙两根熔丝,甲熔断的概率为0.85,乙熔断的概率为0.74,两根同时熔断的概率为0.63,求至少有一根熔断的概率.
解析:设 “甲熔丝熔断”, “乙熔丝熔断”,则“甲、乙两根熔丝中至少有一根熔断”为事件 .
所以P(A∪B)=P(A)+P(B)- (A∩B)= 0.85+0.74-0.63=0.96.
我们知道,事件的关系、运算与集合的关系、运算十分类似,在它们之间可以建立一个对应关系.因此,可以从集合的观点来看待事件.比如不可能事件对应于空集 ;必然事件对应于全集 ;事件 与 之并对应于两个集合的并 ;事件与 之交对应于两个集合的交等.
这样,类比集合中的容斥原理:
Card( A∪B )= Card (A)+ Card (B)- Card (A∩B)
可以得到概率加法公式的一般形式:
P(A∪B)=P(A)+P(B)- (A∩B) .
特别地,若事件 与 是互斥事件,则 是不可能事件,有 P(A∩B)=0 ,这时P(A∪B)=P(A)+P(B) ,即是互斥事件的概率加法公式.
课堂小结
3.当两个事件不互斥时,推论:P(A+B+C)=P(A)+P (B) +P (C)-
P(AB)- P(AC)- P(BC)+ P(ABC)
1.当两个事件互斥时
P(A+B)= P(A)+ P(B)
2.当两个事件不互斥时
P(A+B)= P(A)+ P(B)-P(AB)
思想和方法总结
做题先要判断两个事件是否是互斥事件,如果是互斥
P(A+B)= P(A)+ P(B)
如果不互斥
P(A+B)= P(A)+ P(B)-P(AB)
课堂练习
1.射手甲一次击中目标的概率为0.7,射手乙一次击中目标的概率为0.5,现在甲、乙两人同时向一个目标射击一次,则目标被击中概率是 .甲、乙都击不中目标的概率是 .
0.05
0 .95
2.打靶时甲每打10次可击中8次,乙每打10次可击中7次,若两人同时射击一个目标,他们都中靶的概率是 .
14/25
3. 甲、乙两门高射炮同时向一敌机开炮,已知甲击中敌机的概率为0.6,乙击中敌机的概率为0.8,甲、乙同时击中敌机的概率为0.48,求敌机被击中的概率.
解析:设 “甲击中敌机”, “乙击中敌机”,则“两人至少有一人击中敌机”为事件 .
所以 P(A∪B)=P(A)+P(B)- (A∩B)= 0.6+0.6-0.36=0.84.
故两人都击不中为 1- P(A∪B)=1-0.84=0.16.
4.某储蓄卡的密码是1中4位数字号码,每位上的数字可以在0,1,2,……9这10个数字中选取
⑴使用该储蓄卡时随意按下1个4位数字,正好按对密码的概率是多少?
⑵某人未记准储蓄卡密码的最后一位,如果他在使用时随意按下一个数字,正好按对的概率是多少?
(1)1/10000,(2)10/1.
5.如图,在一段电路中并联着3个电池作为电源,如果其中1个或2个损环电路仍能正常工作,已知电池A,B,C损坏的概率均为0.7,求电路正常工作的概率,并分析为什么选择并联电路?
A
B
C
解析:P=1-(1-0.7)(1-0.7)(1-0.7)=0.973;由于并联电路的稳定性,除非3个电池全部损坏,否则电路仍然能正常工作.
甲、乙、丙三名同学,在数学课后独立完成6道同步练习题,甲及格的概率为0.8,乙及格的概率为0.6,丙及格的概率为0.7,则现在三人各答一道题,则三人中只有一人及格的概率为 .
47/250
针对性练习
