沪科版数学七年级下册8.4.1因式分解课件(共18张PPT)
文档属性
| 名称 | 沪科版数学七年级下册8.4.1因式分解课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 17:00:06 | ||
图片预览






文档简介
(共18张PPT)
(1)
(2)
30=2x3x( )
6=2x( )
整数的因数分解
3
5
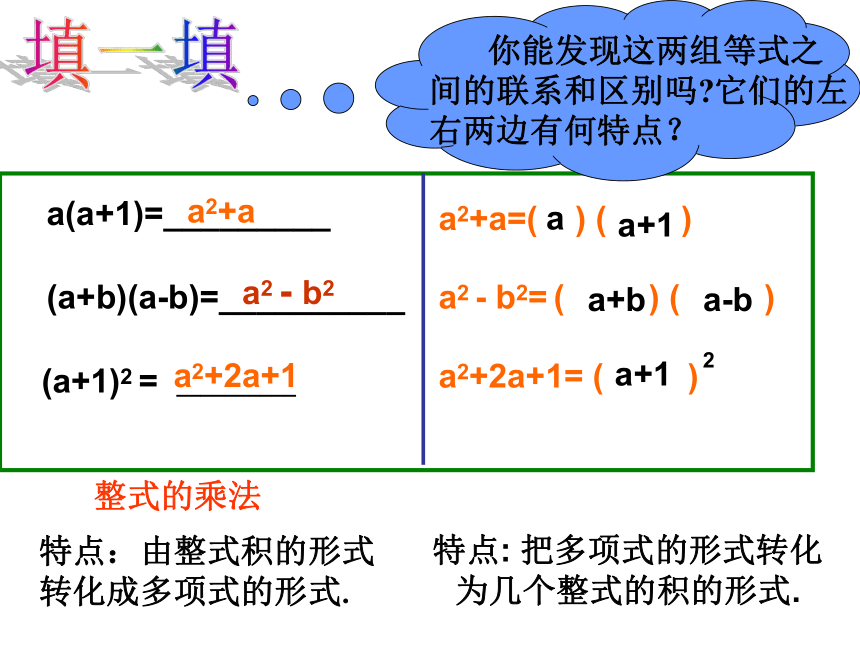
a(a+1)=_________
(a+b)(a-b)=__________
(a+1)2 = __________
a2 - b2
a2+2a+1
a2+a
a
a+1
a+b
a-b
a+1
整式的乘法
特点: 把多项式的形式转化为几个整式的积的形式.
特点:由整式积的形式转化成多项式的形式.
2
像这样,把一个多项式化成几个整式的积的形式,叫做因式分解,也叫做把这个多项式分解因式。
2a(a-1)
(a+3)2
(2+a)(2-a)
a2+6a+9
4-a2
将下列相等的整式连线。
2a2-2a
是
不是
是
不是
不是
不是
下列代数式从左到右的变形是因式分解吗?
(6)18a3bc=3a2b·6ac
(2) 4x2-4x+1=(2x+1)2
(3)a2-9=(a+3)(a-3)
找一找下列各多项式公有的因式是什么?
3
a
a2
2m
3m4
2ab
公因式:
每一项都含有的相同的整式
⑦(x+y)2+(x+y)3
(x+y)2
公因式的确定方法:
系数:
字母:
例1、用提公因式法对下列多项式进行因式分解
(1) 3a2-9ab
(2)24x2m2-16xm3
(3)-5a2+25a
(4)-ab2c3-7a3bc2
(5)anb2+an+1b
=3a(a-3b)
=8xm2(3x-2m)
=-5a·a-5a·(-5)
取各系数的最大公约数
取相同字母的最低次幂
=8xm2·3x-8xm2·2m
=3a·a-3a·3b
=-5a(a-5)
练习
1、填空:
⑴6x3-18x2= (x-3)
⑵-7a2+21a=-7a( )
2、把下列各式分解因式:
⑴np-nq
⑵-x3y-x2y2+xy
=n
=-xy
(p-q)
(x2+xy-1)
6x2
a-3
992+99
(1)
(2)
=259
=9900
判断:下面是甲、乙、丙三位同学对多项式3x2y5+2x3y4z2的分解结果,回答问题:
⑴他们提出的是否是公因式?
⑵他们中谁分解的对?谁分解的不对?
为什么?
甲:3x2y5+2x3y4z2=x2(3y5+2xy4z2)
乙:3x2y5+2x3y4z2=x2y3(3y2+2xyz2)
丙:3x2y5+2x3y4z2=x2y4(3y+2xz2)
2、因式分解要注意以下几点:
3)、要分解到不能分解为止
2)、分解的结果一定是几个整式的乘积的 形式
1)、分解的对象必须是多项式
1、因式分解与整式乘法是互逆过程.
例2
⑵ 3n(x-2)+(2-x)
把下列各式分解因式:
⑴ 2x(b+c)-3y(b+c)
=(b+c)(2x-3y)
=3n(x-2)-(x-2)
=(x-2)(3n-1)
你能把这题因式分解吗?
9(m-n)2-12(n-m)3
=3(m-n)2[3+4(m-n)]
=3(m-n)2(3+4m-4n)
=9(m-n)2+12(m-n)3
1、 m(a-b)-n(a-b)
2、3(a+b)2+6(a+b)
3、 6(x-y)3-3y(y-x)2
4、 mn(m-n)-m(n-m)2
⑴因式分解的概念;
数学思想:“类比” 与“化归”
本节课我们共同学习了:
⑵因式分解与整式乘法的区别与联系;
⑶公因式及找公因式的方法;
⑷提公因式法分解因式及应注意的问题.
? 2、 兴趣题:手工课上,老师给同学们发了3张正方形纸片,3张长方形纸片,请你将它们拼成一个长方形,并运用面积之间的关系,将多项式2a2+3ab+b2 因式分解
1、课本P78 习题8.4第1、2题
作业
祝同学们:好好学习,天天向上。
(1)
(2)
30=2x3x( )
6=2x( )
整数的因数分解
3
5
a(a+1)=_________
(a+b)(a-b)=__________
(a+1)2 = __________
a2 - b2
a2+2a+1
a2+a
a
a+1
a+b
a-b
a+1
整式的乘法
特点: 把多项式的形式转化为几个整式的积的形式.
特点:由整式积的形式转化成多项式的形式.
2
像这样,把一个多项式化成几个整式的积的形式,叫做因式分解,也叫做把这个多项式分解因式。
2a(a-1)
(a+3)2
(2+a)(2-a)
a2+6a+9
4-a2
将下列相等的整式连线。
2a2-2a
是
不是
是
不是
不是
不是
下列代数式从左到右的变形是因式分解吗?
(6)18a3bc=3a2b·6ac
(2) 4x2-4x+1=(2x+1)2
(3)a2-9=(a+3)(a-3)
找一找下列各多项式公有的因式是什么?
3
a
a2
2m
3m4
2ab
公因式:
每一项都含有的相同的整式
⑦(x+y)2+(x+y)3
(x+y)2
公因式的确定方法:
系数:
字母:
例1、用提公因式法对下列多项式进行因式分解
(1) 3a2-9ab
(2)24x2m2-16xm3
(3)-5a2+25a
(4)-ab2c3-7a3bc2
(5)anb2+an+1b
=3a(a-3b)
=8xm2(3x-2m)
=-5a·a-5a·(-5)
取各系数的最大公约数
取相同字母的最低次幂
=8xm2·3x-8xm2·2m
=3a·a-3a·3b
=-5a(a-5)
练习
1、填空:
⑴6x3-18x2= (x-3)
⑵-7a2+21a=-7a( )
2、把下列各式分解因式:
⑴np-nq
⑵-x3y-x2y2+xy
=n
=-xy
(p-q)
(x2+xy-1)
6x2
a-3
992+99
(1)
(2)
=259
=9900
判断:下面是甲、乙、丙三位同学对多项式3x2y5+2x3y4z2的分解结果,回答问题:
⑴他们提出的是否是公因式?
⑵他们中谁分解的对?谁分解的不对?
为什么?
甲:3x2y5+2x3y4z2=x2(3y5+2xy4z2)
乙:3x2y5+2x3y4z2=x2y3(3y2+2xyz2)
丙:3x2y5+2x3y4z2=x2y4(3y+2xz2)
2、因式分解要注意以下几点:
3)、要分解到不能分解为止
2)、分解的结果一定是几个整式的乘积的 形式
1)、分解的对象必须是多项式
1、因式分解与整式乘法是互逆过程.
例2
⑵ 3n(x-2)+(2-x)
把下列各式分解因式:
⑴ 2x(b+c)-3y(b+c)
=(b+c)(2x-3y)
=3n(x-2)-(x-2)
=(x-2)(3n-1)
你能把这题因式分解吗?
9(m-n)2-12(n-m)3
=3(m-n)2[3+4(m-n)]
=3(m-n)2(3+4m-4n)
=9(m-n)2+12(m-n)3
1、 m(a-b)-n(a-b)
2、3(a+b)2+6(a+b)
3、 6(x-y)3-3y(y-x)2
4、 mn(m-n)-m(n-m)2
⑴因式分解的概念;
数学思想:“类比” 与“化归”
本节课我们共同学习了:
⑵因式分解与整式乘法的区别与联系;
⑶公因式及找公因式的方法;
⑷提公因式法分解因式及应注意的问题.
? 2、 兴趣题:手工课上,老师给同学们发了3张正方形纸片,3张长方形纸片,请你将它们拼成一个长方形,并运用面积之间的关系,将多项式2a2+3ab+b2 因式分解
1、课本P78 习题8.4第1、2题
作业
祝同学们:好好学习,天天向上。
