沪科版八下数学17.1一元二次方程教学课件(40张)
文档属性
| 名称 | 沪科版八下数学17.1一元二次方程教学课件(40张) |  | |
| 格式 | zip | ||
| 文件大小 | 830.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 11:41:58 | ||
图片预览










文档简介
(共40张PPT)
第17章 一元二次方程
17.1 一元二次方程
课堂讲解
课时流程
1
2
一元二次方程的定义
一元二次方程的一般形式
一元二次方程的解(根)
逐点
导讲练
课堂小结
课后
作业
某蔬菜队2009年全年无公害蔬菜产量为100 t,计划2011年无公害蔬菜的产量比2009年翻一番(即为200 t).要实现这一目标,2010年和2011年无公害蔬菜产 量的年平均增长率应是多少?
设这个队2010?2011年无公害蔬菜产量的年平均增长率是x,问题可以归结为求解方程
x2+2x-1=0.
上述方程不是一次的,如何求解呢?
本章将学习一元二次方程的有关知识,它可以用来解决像上面这样的一些实际问题.
知1-导
1
知识点
一元二次方程的定义
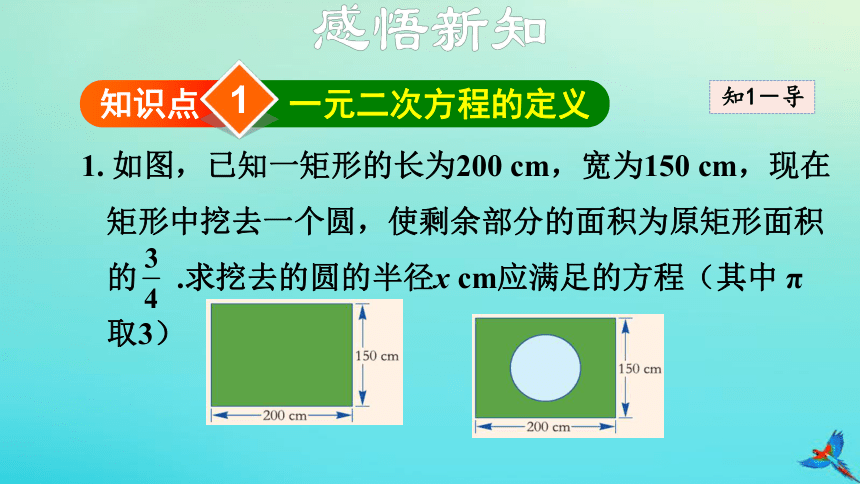
1. 如图,已知一矩形的长为200 cm,宽为150 cm,现在矩形中挖去一个圆,使剩余部分的面积为原矩形面积的 .求挖去的圆的半径x cm应满足的方程(其中 π取3)
知1-导
设 _______________________________________
找等量关系:_______________________________
列出方程:______________________________①
2. 据某市交通部门统计,前年该市汽车拥有量为75万辆,两年后增加到108万辆.求该市两年来汽车拥有量的年平均增长率x应满足的方程.
等量关系:______________________________
列出方程: ___________________________ ②
知1-讲
定义:只含有一个未知数,并且未知数的最高次数是2的整式方程,叫做一元二次方程.
知1-讲
要点精析:
(1)理解定义,要掌握三个关键点:整式、未知数个数及最高次数;“一元”是指整个方程中只含有一个未知数;“二次”是指该未知数的最高次数是2.
(2)一元二次方程的识别方法:
整理前:①整式方程,②只含一个未知数;
整理后:未知数的最高次数是2.
知1-讲
下列方程:
①x2+y-6=0;②x2+ =2;③x2-x-2=0;
④x2-2+5x3-6x=0;⑤2x2-3x=2(x2-2),
其中是一元二次方程的有( )
A.1个 B. 2个 C.3个 D.4个
例1
A
知1-讲
要判断一个方程是否是一元二次方程,要从原方程及整理后的方程两方面进行判断,看其是否符合一元二次方程的条件.①中有两个未知数;②不是整式方程;④未知数的最高次数是3;⑤整理后二次项系数为零.
导引:
知1-讲
判断一个方程是否是一元二次方程,有两个关键点:
(1)整理前是整式方程且只含一个未知数;
(2) 整理后未知数的最高次数是2.
本例⑤2x2-3x=2(x2-2)中易出现不整理就下结论,误认为是一元二次方程的错误.
知1-讲
因为已知的方程是一元二次方程,所以未知数x的最高次数是2,即a-3=2,所以a=5.
导引:
已知关于x的方程xa-3-2x +1=0是一元二次方程,则a=________.
例2
5
知1-讲
已知某方程为一元二次方程,则此方程必须符合一元二次方程的两个基本特征:只含一个未知数;未知数的最高次数是2.当二次项系数是待定系数时,还要考虑二次项系数不等于0.
知1-练
D
1 下列关于x的方程一定是一元二次方程的是( )
A.ax2+bx+c=0 B.x2+1-x2=0
C.x2+ =2 D.x2-x-2=0
知1-练
D
3 若关于x的方程(a-2) x2-2ax+a+2=0是一元二次方程,则( )
A.a=2 B.a=-2
C.a=0 D.a≠2
知1-练
B
4 若方程(m-1)x|m|+1-2x=3是关于x的一元二次方程,则有( )
A.m=1 B.m=-1
C.m=±1 D.m≠±1
2
知识点
一元二次方程的一般形式
知2-讲
1.一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式:ax2+bx+c=0(a≠0).这种形式叫做一元二次方程的一般形式,其中ax2叫做二次项,a是二次项的系数;bx叫做一次项,b是一次项的系数;c叫做常数项.
知2-讲
要点精析:
(1)ax2+bx+c=0,当a≠0时,方程才是一元二次方程,但b,c可以是0.
(2)可以通过去分母、去括号、移项、合并同类项等步骤将一个一元二次方程化成一般形式.
知2-讲
要点精析:
(3)指出一元二次方程的某项时,含未知数的项应连同系数一起;指出某项的系数时,应连同它前面的符号一起.
(4)二次项系数不等于零既是一元二次方程的必要条件,也是一个隐含条件.
知2-讲
例3
把方程3x(x-1)=2(x-2)-4化成一般形式, 并写出它的二次项系数、一次项系数及常数项.
去括号,得3x2-3x=2x-4-4.
移项,合并同类项,得方程的一般形式:
3x2-5x+8=0.
它的二次项系数是3,一次项系数是-5,常数项是8.
解:
知2-讲
1.化一般形式一般要经历一去(去分母、去括号)、二移、三并这三步;
2.当整理为一般形式后,如果二次项系数是负数,一般要把它转化为正数,若有关系数是分数,一般要把它转化为整数.
知2-讲
例4
已知关于x的方程(a2-1)x2+(1-a)x+a-2=0.
(1)当a为何值时,该方程为一元二次方程?
(2)当a为何值时,该方程为一元一次方程?并求一元一次方程的解.
知2-讲
导引:
已知条件中说明是关于x的方程,则方程中只含
有一个未知数,并且未知数的最高次数是2,但
由于二次项系数待定,故分析二次项系数为不为
零是确定该方程是否为一元二次方程的关键点.
知2-讲
(来自教材)
(1)由题意得a2-1≠0,
即a≠±1时,该方程为一元二次方程.
(2)由题意得a2-1=0且1-a≠0,解得a=-1,
即当a=-1时,该方程为一元一次方程.
此时方程为2x-3=0,
解得x=
解:
知2-讲
在一元二次方程的一般形式ax2+bx+c=0中,a≠0是确定该方程为一元二次方程的唯一标准,在应用一元二次方程的定义求待定字母的值时,既要考虑未知数的最高次数是2,又要考虑二次项系数不为零.
知2-讲
例5
〈易错题〉关于x的一元二次方程(a-2)x2+3x+a2-4=0的常数项为0,求a的值.
知2-讲
∵关于x的一元二次方程(a-2)x2+3x+a2-4=0的常数项为0,
∴a2-4=0,∴a=±2.
错解中只应用了题中常数项为0这一直观条
件,题目的前提条件说明该方程是一元二次方
程,忽略了一元二次方程的二次项系数不为零
这一隐含条件.
错解:
错解分析:
知2-讲
∵关于x的一元二次方程
(a-2)x2+3x+a2-4=0的常数项为0,
∴ 解得a=-2.
正解:
知2-讲
在解由一元二次方程的定义求有关待定字母的值时,先要把方程整理成一元二次方程的一般形式,再由题中给出的条件及二次项系数不为零列式求解.
1 将下列一元二次方程化成一般形式,并指出它们的二次项系数、一次项系数及常数项:
(1)5x2=6x-8;
(2)
(3) x(x-1)=0;
知2-练
知2-练
A
2 把方程x(x+2)=5(x-2)化成一般形式,则a,b,c的值分别是( )
A.1,-3,10 B.1,7,-10
C.1,-5,12 D.1,3,2
知2-练
2
3 一元二次方程-2(x-1)2=x+3化成一般形式
ax2+bx+c=0后,若a=2,则b+c的值是________.
4 若一元二次方程(2a-4)x2+(3a+6)x+a-8=0没有一次项,则a的值为_______.
-2
知3-讲
3
知识点
一元二次方程的解(根)
1.定义:能使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解(根).
要点精析:
(1)判定某个数是方程的根的必要条件:使方程左右两边相等.
(2)根据方程的根的定义可以判断解出的方程的根是否正确.
(3)一元二次方程的根不止一个,只要符合条件的都是方程的根.
知3-讲
根据一元二次方程的根的定义,将这些数作为
未知数的值分别代入方程,能够使方程左右两
边相等的数就是方程的根.
-1,3是方程 x2-2x-3=0的根.
例6
导引:
下面哪些数是方程 x2-2x-3=0的根?
-3,-2,-1,0,1,2,3
解:
知3-讲
检验一个数是否为方程的解或根,只要把这个数分别代入方程的左右两边算出数值,看它们是否相等.在找解时注意使一元二次方程左右两边相等的未知数的值不一定只有一个.
知3-讲
根据方程的根的意义,将x=2直接代入方程的左
右两边,就可得到以b为未知数的一元一次方程,
求解即可.
例7
导引:
如果2是一元二次方程x2+bx+2=0的一个根,那么字母b的值为( )
A. 3 B. -3 C. 4 D.-4
B
知3-讲
方程的根就是满足方程左右两边相等的未知数的值,因此求含有字母系数的一元二次方程中的字母的值时,只需把已知方程的根代入原方程就可求岀相关的待定字母的值.
知3-练
1 下面哪些数是方程x2+x-2=0的根?
-3,-2,-1,0,1,2,3
2 (中考·重庆)一元二次方程x2-2x=0的根是( )
A.x1=0,x2=-2 B.x1=1,x2=2
C.x1=1,x2=-2 D.x1=0,x2=2
-2,1
D
知3-练
3 (中考·攀枝花)若x=-2是关于x的一元二次方程x2+ -a2=0的一个根,则a的值为( )
A.-1或4 B.-1或-4
C.1或-4 D.1或4
C
1. 一元二次方程的概念.
一元二次方程的定义要求的三个条件。要灵活运用定义判断方程是一元二次方程或由一元二次方程来确定一些字母的值及取值范围
2. 一元二次方程的一般形式ax2+bx+c=0(a≠0)和二次项、 二次项系数,一次项、一次项系数,常数项的概念.
3.一元二次方程根的概念以及作用.
第17章 一元二次方程
17.1 一元二次方程
课堂讲解
课时流程
1
2
一元二次方程的定义
一元二次方程的一般形式
一元二次方程的解(根)
逐点
导讲练
课堂小结
课后
作业
某蔬菜队2009年全年无公害蔬菜产量为100 t,计划2011年无公害蔬菜的产量比2009年翻一番(即为200 t).要实现这一目标,2010年和2011年无公害蔬菜产 量的年平均增长率应是多少?
设这个队2010?2011年无公害蔬菜产量的年平均增长率是x,问题可以归结为求解方程
x2+2x-1=0.
上述方程不是一次的,如何求解呢?
本章将学习一元二次方程的有关知识,它可以用来解决像上面这样的一些实际问题.
知1-导
1
知识点
一元二次方程的定义
1. 如图,已知一矩形的长为200 cm,宽为150 cm,现在矩形中挖去一个圆,使剩余部分的面积为原矩形面积的 .求挖去的圆的半径x cm应满足的方程(其中 π取3)
知1-导
设 _______________________________________
找等量关系:_______________________________
列出方程:______________________________①
2. 据某市交通部门统计,前年该市汽车拥有量为75万辆,两年后增加到108万辆.求该市两年来汽车拥有量的年平均增长率x应满足的方程.
等量关系:______________________________
列出方程: ___________________________ ②
知1-讲
定义:只含有一个未知数,并且未知数的最高次数是2的整式方程,叫做一元二次方程.
知1-讲
要点精析:
(1)理解定义,要掌握三个关键点:整式、未知数个数及最高次数;“一元”是指整个方程中只含有一个未知数;“二次”是指该未知数的最高次数是2.
(2)一元二次方程的识别方法:
整理前:①整式方程,②只含一个未知数;
整理后:未知数的最高次数是2.
知1-讲
下列方程:
①x2+y-6=0;②x2+ =2;③x2-x-2=0;
④x2-2+5x3-6x=0;⑤2x2-3x=2(x2-2),
其中是一元二次方程的有( )
A.1个 B. 2个 C.3个 D.4个
例1
A
知1-讲
要判断一个方程是否是一元二次方程,要从原方程及整理后的方程两方面进行判断,看其是否符合一元二次方程的条件.①中有两个未知数;②不是整式方程;④未知数的最高次数是3;⑤整理后二次项系数为零.
导引:
知1-讲
判断一个方程是否是一元二次方程,有两个关键点:
(1)整理前是整式方程且只含一个未知数;
(2) 整理后未知数的最高次数是2.
本例⑤2x2-3x=2(x2-2)中易出现不整理就下结论,误认为是一元二次方程的错误.
知1-讲
因为已知的方程是一元二次方程,所以未知数x的最高次数是2,即a-3=2,所以a=5.
导引:
已知关于x的方程xa-3-2x +1=0是一元二次方程,则a=________.
例2
5
知1-讲
已知某方程为一元二次方程,则此方程必须符合一元二次方程的两个基本特征:只含一个未知数;未知数的最高次数是2.当二次项系数是待定系数时,还要考虑二次项系数不等于0.
知1-练
D
1 下列关于x的方程一定是一元二次方程的是( )
A.ax2+bx+c=0 B.x2+1-x2=0
C.x2+ =2 D.x2-x-2=0
知1-练
D
3 若关于x的方程(a-2) x2-2ax+a+2=0是一元二次方程,则( )
A.a=2 B.a=-2
C.a=0 D.a≠2
知1-练
B
4 若方程(m-1)x|m|+1-2x=3是关于x的一元二次方程,则有( )
A.m=1 B.m=-1
C.m=±1 D.m≠±1
2
知识点
一元二次方程的一般形式
知2-讲
1.一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式:ax2+bx+c=0(a≠0).这种形式叫做一元二次方程的一般形式,其中ax2叫做二次项,a是二次项的系数;bx叫做一次项,b是一次项的系数;c叫做常数项.
知2-讲
要点精析:
(1)ax2+bx+c=0,当a≠0时,方程才是一元二次方程,但b,c可以是0.
(2)可以通过去分母、去括号、移项、合并同类项等步骤将一个一元二次方程化成一般形式.
知2-讲
要点精析:
(3)指出一元二次方程的某项时,含未知数的项应连同系数一起;指出某项的系数时,应连同它前面的符号一起.
(4)二次项系数不等于零既是一元二次方程的必要条件,也是一个隐含条件.
知2-讲
例3
把方程3x(x-1)=2(x-2)-4化成一般形式, 并写出它的二次项系数、一次项系数及常数项.
去括号,得3x2-3x=2x-4-4.
移项,合并同类项,得方程的一般形式:
3x2-5x+8=0.
它的二次项系数是3,一次项系数是-5,常数项是8.
解:
知2-讲
1.化一般形式一般要经历一去(去分母、去括号)、二移、三并这三步;
2.当整理为一般形式后,如果二次项系数是负数,一般要把它转化为正数,若有关系数是分数,一般要把它转化为整数.
知2-讲
例4
已知关于x的方程(a2-1)x2+(1-a)x+a-2=0.
(1)当a为何值时,该方程为一元二次方程?
(2)当a为何值时,该方程为一元一次方程?并求一元一次方程的解.
知2-讲
导引:
已知条件中说明是关于x的方程,则方程中只含
有一个未知数,并且未知数的最高次数是2,但
由于二次项系数待定,故分析二次项系数为不为
零是确定该方程是否为一元二次方程的关键点.
知2-讲
(来自教材)
(1)由题意得a2-1≠0,
即a≠±1时,该方程为一元二次方程.
(2)由题意得a2-1=0且1-a≠0,解得a=-1,
即当a=-1时,该方程为一元一次方程.
此时方程为2x-3=0,
解得x=
解:
知2-讲
在一元二次方程的一般形式ax2+bx+c=0中,a≠0是确定该方程为一元二次方程的唯一标准,在应用一元二次方程的定义求待定字母的值时,既要考虑未知数的最高次数是2,又要考虑二次项系数不为零.
知2-讲
例5
〈易错题〉关于x的一元二次方程(a-2)x2+3x+a2-4=0的常数项为0,求a的值.
知2-讲
∵关于x的一元二次方程(a-2)x2+3x+a2-4=0的常数项为0,
∴a2-4=0,∴a=±2.
错解中只应用了题中常数项为0这一直观条
件,题目的前提条件说明该方程是一元二次方
程,忽略了一元二次方程的二次项系数不为零
这一隐含条件.
错解:
错解分析:
知2-讲
∵关于x的一元二次方程
(a-2)x2+3x+a2-4=0的常数项为0,
∴ 解得a=-2.
正解:
知2-讲
在解由一元二次方程的定义求有关待定字母的值时,先要把方程整理成一元二次方程的一般形式,再由题中给出的条件及二次项系数不为零列式求解.
1 将下列一元二次方程化成一般形式,并指出它们的二次项系数、一次项系数及常数项:
(1)5x2=6x-8;
(2)
(3) x(x-1)=0;
知2-练
知2-练
A
2 把方程x(x+2)=5(x-2)化成一般形式,则a,b,c的值分别是( )
A.1,-3,10 B.1,7,-10
C.1,-5,12 D.1,3,2
知2-练
2
3 一元二次方程-2(x-1)2=x+3化成一般形式
ax2+bx+c=0后,若a=2,则b+c的值是________.
4 若一元二次方程(2a-4)x2+(3a+6)x+a-8=0没有一次项,则a的值为_______.
-2
知3-讲
3
知识点
一元二次方程的解(根)
1.定义:能使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解(根).
要点精析:
(1)判定某个数是方程的根的必要条件:使方程左右两边相等.
(2)根据方程的根的定义可以判断解出的方程的根是否正确.
(3)一元二次方程的根不止一个,只要符合条件的都是方程的根.
知3-讲
根据一元二次方程的根的定义,将这些数作为
未知数的值分别代入方程,能够使方程左右两
边相等的数就是方程的根.
-1,3是方程 x2-2x-3=0的根.
例6
导引:
下面哪些数是方程 x2-2x-3=0的根?
-3,-2,-1,0,1,2,3
解:
知3-讲
检验一个数是否为方程的解或根,只要把这个数分别代入方程的左右两边算出数值,看它们是否相等.在找解时注意使一元二次方程左右两边相等的未知数的值不一定只有一个.
知3-讲
根据方程的根的意义,将x=2直接代入方程的左
右两边,就可得到以b为未知数的一元一次方程,
求解即可.
例7
导引:
如果2是一元二次方程x2+bx+2=0的一个根,那么字母b的值为( )
A. 3 B. -3 C. 4 D.-4
B
知3-讲
方程的根就是满足方程左右两边相等的未知数的值,因此求含有字母系数的一元二次方程中的字母的值时,只需把已知方程的根代入原方程就可求岀相关的待定字母的值.
知3-练
1 下面哪些数是方程x2+x-2=0的根?
-3,-2,-1,0,1,2,3
2 (中考·重庆)一元二次方程x2-2x=0的根是( )
A.x1=0,x2=-2 B.x1=1,x2=2
C.x1=1,x2=-2 D.x1=0,x2=2
-2,1
D
知3-练
3 (中考·攀枝花)若x=-2是关于x的一元二次方程x2+ -a2=0的一个根,则a的值为( )
A.-1或4 B.-1或-4
C.1或-4 D.1或4
C
1. 一元二次方程的概念.
一元二次方程的定义要求的三个条件。要灵活运用定义判断方程是一元二次方程或由一元二次方程来确定一些字母的值及取值范围
2. 一元二次方程的一般形式ax2+bx+c=0(a≠0)和二次项、 二次项系数,一次项、一次项系数,常数项的概念.
3.一元二次方程根的概念以及作用.
