沪科版八下数学17.4一元二次的根与系数的关系教学课件(33张)
文档属性
| 名称 | 沪科版八下数学17.4一元二次的根与系数的关系教学课件(33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 824.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 00:00:00 | ||
图片预览









文档简介
(共33张PPT)
第17章 一元二次方程
17.4 一元二次方程的根与系数的关系
课堂讲解
课时流程
1
2
一元二次方程的根与系数的关系
一元二次方程的根与系数关系的应用
逐点
导讲练
课堂小结
课后
作业
学生自主预习教材,完成下列各题. 1.一元二次方程ax2+bx+c=0 (a≠0),
在b2-4ac≥0的条件下,它的根为 ,
这个式子叫作一元二次方程的求根公式.
2.对于一元二次方程ax2+bx+c=0 (a≠0),
当 时,方程有两个 的实数根;
当 时,方程有两个 的实数根;
当 时,方程 实数根.
知1-导
1
知识点
一元二次方程的根与系数的关系
探究
在前面17.2节中,我们学过,一元二次方程的每一个根都可由它的各项系数通过运算得到.
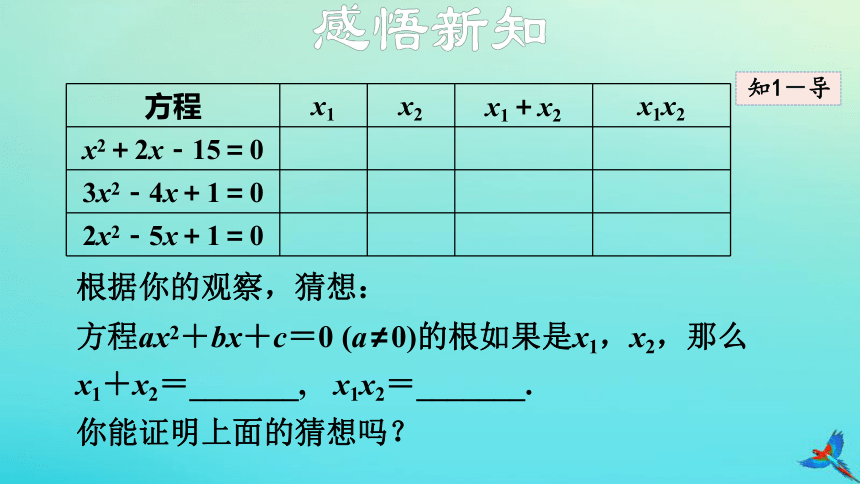
进一步,你是否注意到每个方程中的两根之和(x1+x2)、两根之积(x1x2)与该方程的各项系数之间有怎样的关系?填写下表,然后观察根与系数的关系:
知1-导
根据你的观察,猜想:
方程ax2+bx+c=0 (a≠0)的根如果是x1,x2,那么
x1+x2=_______, x1x2=_______.
你能证明上面的猜想吗?
方程 x1 x2 x1+x2 x1x2
x2+2x-15=0
3x2-4x+1=0
2x2-5x+1=0
知1-讲
一元二次方程根与系数的关系:
如果ax2+bx+c=0(a≠0)的两个根为x1,x2,
那么x1+x2= ,x1x2= .
这个关系通常称为韦达定理.
知1-讲
要点精析:
(1)一元二次方程的根与系数的关系的前提条件是二次项系数不为0和方程有实数根.
(2)根与系数的关系刻画了一元二次方程的两根和、
两根积与系数a,b,c之间的关系.
知1-讲
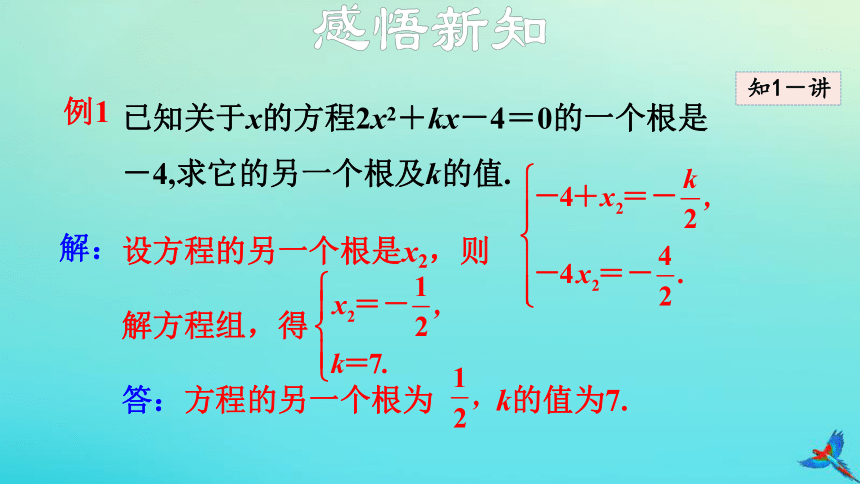
设方程的另一个根是x2,则
解方程组,得
答:方程的另一个根为 k的值为7.
例1
已知关于x的方程2x2+kx-4=0的一个根是-4,求它的另一个根及k的值.
解:
知1-讲
已知方程的一根求另一根,可以直接代入先求方程中待定字母的值,然后再解方程求另一根.也可以直接利用根与系数的关系求另一根及待定字母的值.
知1-讲
例2
〈德州〉方程x2+2kx+k2-2k+1=0的两个实数根x1,x2满足x12+x22 =4则k的值为________.
1
知1-讲
由x12+x22=x12+2x1·x2+x22-2x1·x2=(x1+x2)2-2x1·x2=4,根据根与系数的关系即可得到一个关于k的方程,从而求得k的值.
∵x12+x22=x12+2x1·x2+x22-2x1·x2
=(x1+x2)2-2x1·x2=4,
x1+x2=-2k,x1·x2=k2-2k+1,
∴4k2-2(k2-2k+1)=4,
解得k=1或k=-3(不合题意,舍去).
导引:
知1-讲
已知方程两根的关系求待定字母系数的值时,
先根据根与系数的关系用待定的字母表示两根之和与两根之积,然后将已知两根的关系进行变形,再将两根的和与积整体代入,列出以待定字母为未知数的方程,进而求出待定字母的值.
知1-练
1 下列各方程中,两根之和与两根之积各是多少?
(1) x2-3x+1=0; (2) 3x2-2x-2=0;
(3) 2x2-9x+5=0; (4) 4x2-7x+1=0;
(5) 2x2+3x=0; (6) 3x2=1.
知1-练
D
2 (中考·金华)一元二次方程x2+4x-3=0的两根为
x1,x2,则x1·x2的值是( )
A.4 B.-4 C.3 D.-3
知1-练
C
3 已知方程x2-2x-1=0,则此方程( )
A.无实数根 B.两根之和为-2
C.两根之积为-1 D.有一根为-1+
知1-练
A
4 (中考·广西)已知实数x1,x2满足x1+x2=7,x1x2=12,则以x1,x2为根的一元二次方程是( )
A.x2-7x+12=0 B.x2+7x+12=0
C.x2+7x-12=0 D.x2-7x-12=0
知2-讲
2
知识点
一元二次方程的根与系数的关系的应用
利用根与系数的关系可以不解方程而求出与两根有关系的一些代数式(对称式)的值.
知2-讲
拓展:常见的涉及一元二次方程的两个根x1,x2的代数式的重要变形有:
①x12+x22=(x1+x2)2-2x1·x2;
知2-讲
④(x1-x2)2=(x1+x2)2-4x1·x2;
⑤(x1+k)(x2+k)=x1·x2+k(x1+x2)+k2;
知2-讲
由韦达定理,得
例3
方程 2x2-3x+1=0的两个根记作x1 , x2不解方程,求x1 -x2的值.
解:
知2-讲
求与根有关的代数式的值时,看代数式是否具有对称性,若具有对称性,则直接变形,将两根之和或积代入求值;若不具有对称性,则将其中的某一个根单独代入方程中,得到与待求值的代数式相关的结构,进行整体代入求值.
知2-讲
例4
已知x1,x2是关于x的一元二次方程kx2+4x-3=0
的两个不相等的实数根.
(1)求k的取值范围.
(2)是否存在这样的实数k,使2x1+2x2- =2 成立?若存在,求出k的值;若不存在,说明理由.
知2-讲
导引:
(1)根据方程有两个不相等的实数根得Δ>0,可求出k的取值范围,同时注意k≠0;
(2)先假设存在,根据根与系数的关系列出以k为未知数的方程,求出k的值,然后结合(1)中k的取值范围检验.
知2-讲
解:
(1)由题意得Δ=42-4k·(-3)>0,∴k>
又k≠0,∴k> 且k≠0.
(2)存在.
∵x1+x2= x1x2= 2x1+2x2-
∴ +k=2,
解得k1=4,k2=-2(不符合题意,舍去).
∴k=4.
知2-讲
根的判别式与根与系数的关系经常结合在一起考查,因为运用根与系数的关系的前提条件是根的判别式大于或等于零.
知2-练
1 已知关于x的方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值.
知2-练
A
2 (中考·枣庄)已知关于x的一元二次方程x2+mx+n=0的两实数根分别为x1=-2,x2=4,则m+n的值是( )
A.-10 B.10 C.-6 D.2
知2-练
D
3 (中考·雅安)已知关于x的一元二次方程x2+mx-8=0的一个实数根为2,则另一个实数根及m的值分别为( )
A.4,-2 B.-4,-2
C.4,2 D.-4,2
知2-练
A
4 若关于x的一元二次方程x2+kx+4k2-3=0的两个实数根分别是x1,x2,且满足x1+x2=x1x2,则k的值为( )
A.-1或 B.-1 C. D.不存在
知2-练
B
5 (中考·烟台)等腰三角形三边长分别为a,b,2,且a,b是关于x的一元二次方程x2-6x+n-1=0的两根,则n的值为( )
A.9 B.10 C.9或10 D.8或10
一元二次方程根与系数的关系的几种常用变形:
(1)x12+x22=(x1+x2)2-2x1x2;
(2)(x1-x2)2=(x1+x2)2-4x1x2;
(3)(x1+1)(x2+1)=x1x2+(x1+x2)+1;
第17章 一元二次方程
17.4 一元二次方程的根与系数的关系
课堂讲解
课时流程
1
2
一元二次方程的根与系数的关系
一元二次方程的根与系数关系的应用
逐点
导讲练
课堂小结
课后
作业
学生自主预习教材,完成下列各题. 1.一元二次方程ax2+bx+c=0 (a≠0),
在b2-4ac≥0的条件下,它的根为 ,
这个式子叫作一元二次方程的求根公式.
2.对于一元二次方程ax2+bx+c=0 (a≠0),
当 时,方程有两个 的实数根;
当 时,方程有两个 的实数根;
当 时,方程 实数根.
知1-导
1
知识点
一元二次方程的根与系数的关系
探究
在前面17.2节中,我们学过,一元二次方程的每一个根都可由它的各项系数通过运算得到.
进一步,你是否注意到每个方程中的两根之和(x1+x2)、两根之积(x1x2)与该方程的各项系数之间有怎样的关系?填写下表,然后观察根与系数的关系:
知1-导
根据你的观察,猜想:
方程ax2+bx+c=0 (a≠0)的根如果是x1,x2,那么
x1+x2=_______, x1x2=_______.
你能证明上面的猜想吗?
方程 x1 x2 x1+x2 x1x2
x2+2x-15=0
3x2-4x+1=0
2x2-5x+1=0
知1-讲
一元二次方程根与系数的关系:
如果ax2+bx+c=0(a≠0)的两个根为x1,x2,
那么x1+x2= ,x1x2= .
这个关系通常称为韦达定理.
知1-讲
要点精析:
(1)一元二次方程的根与系数的关系的前提条件是二次项系数不为0和方程有实数根.
(2)根与系数的关系刻画了一元二次方程的两根和、
两根积与系数a,b,c之间的关系.
知1-讲
设方程的另一个根是x2,则
解方程组,得
答:方程的另一个根为 k的值为7.
例1
已知关于x的方程2x2+kx-4=0的一个根是-4,求它的另一个根及k的值.
解:
知1-讲
已知方程的一根求另一根,可以直接代入先求方程中待定字母的值,然后再解方程求另一根.也可以直接利用根与系数的关系求另一根及待定字母的值.
知1-讲
例2
〈德州〉方程x2+2kx+k2-2k+1=0的两个实数根x1,x2满足x12+x22 =4则k的值为________.
1
知1-讲
由x12+x22=x12+2x1·x2+x22-2x1·x2=(x1+x2)2-2x1·x2=4,根据根与系数的关系即可得到一个关于k的方程,从而求得k的值.
∵x12+x22=x12+2x1·x2+x22-2x1·x2
=(x1+x2)2-2x1·x2=4,
x1+x2=-2k,x1·x2=k2-2k+1,
∴4k2-2(k2-2k+1)=4,
解得k=1或k=-3(不合题意,舍去).
导引:
知1-讲
已知方程两根的关系求待定字母系数的值时,
先根据根与系数的关系用待定的字母表示两根之和与两根之积,然后将已知两根的关系进行变形,再将两根的和与积整体代入,列出以待定字母为未知数的方程,进而求出待定字母的值.
知1-练
1 下列各方程中,两根之和与两根之积各是多少?
(1) x2-3x+1=0; (2) 3x2-2x-2=0;
(3) 2x2-9x+5=0; (4) 4x2-7x+1=0;
(5) 2x2+3x=0; (6) 3x2=1.
知1-练
D
2 (中考·金华)一元二次方程x2+4x-3=0的两根为
x1,x2,则x1·x2的值是( )
A.4 B.-4 C.3 D.-3
知1-练
C
3 已知方程x2-2x-1=0,则此方程( )
A.无实数根 B.两根之和为-2
C.两根之积为-1 D.有一根为-1+
知1-练
A
4 (中考·广西)已知实数x1,x2满足x1+x2=7,x1x2=12,则以x1,x2为根的一元二次方程是( )
A.x2-7x+12=0 B.x2+7x+12=0
C.x2+7x-12=0 D.x2-7x-12=0
知2-讲
2
知识点
一元二次方程的根与系数的关系的应用
利用根与系数的关系可以不解方程而求出与两根有关系的一些代数式(对称式)的值.
知2-讲
拓展:常见的涉及一元二次方程的两个根x1,x2的代数式的重要变形有:
①x12+x22=(x1+x2)2-2x1·x2;
知2-讲
④(x1-x2)2=(x1+x2)2-4x1·x2;
⑤(x1+k)(x2+k)=x1·x2+k(x1+x2)+k2;
知2-讲
由韦达定理,得
例3
方程 2x2-3x+1=0的两个根记作x1 , x2不解方程,求x1 -x2的值.
解:
知2-讲
求与根有关的代数式的值时,看代数式是否具有对称性,若具有对称性,则直接变形,将两根之和或积代入求值;若不具有对称性,则将其中的某一个根单独代入方程中,得到与待求值的代数式相关的结构,进行整体代入求值.
知2-讲
例4
已知x1,x2是关于x的一元二次方程kx2+4x-3=0
的两个不相等的实数根.
(1)求k的取值范围.
(2)是否存在这样的实数k,使2x1+2x2- =2 成立?若存在,求出k的值;若不存在,说明理由.
知2-讲
导引:
(1)根据方程有两个不相等的实数根得Δ>0,可求出k的取值范围,同时注意k≠0;
(2)先假设存在,根据根与系数的关系列出以k为未知数的方程,求出k的值,然后结合(1)中k的取值范围检验.
知2-讲
解:
(1)由题意得Δ=42-4k·(-3)>0,∴k>
又k≠0,∴k> 且k≠0.
(2)存在.
∵x1+x2= x1x2= 2x1+2x2-
∴ +k=2,
解得k1=4,k2=-2(不符合题意,舍去).
∴k=4.
知2-讲
根的判别式与根与系数的关系经常结合在一起考查,因为运用根与系数的关系的前提条件是根的判别式大于或等于零.
知2-练
1 已知关于x的方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值.
知2-练
A
2 (中考·枣庄)已知关于x的一元二次方程x2+mx+n=0的两实数根分别为x1=-2,x2=4,则m+n的值是( )
A.-10 B.10 C.-6 D.2
知2-练
D
3 (中考·雅安)已知关于x的一元二次方程x2+mx-8=0的一个实数根为2,则另一个实数根及m的值分别为( )
A.4,-2 B.-4,-2
C.4,2 D.-4,2
知2-练
A
4 若关于x的一元二次方程x2+kx+4k2-3=0的两个实数根分别是x1,x2,且满足x1+x2=x1x2,则k的值为( )
A.-1或 B.-1 C. D.不存在
知2-练
B
5 (中考·烟台)等腰三角形三边长分别为a,b,2,且a,b是关于x的一元二次方程x2-6x+n-1=0的两根,则n的值为( )
A.9 B.10 C.9或10 D.8或10
一元二次方程根与系数的关系的几种常用变形:
(1)x12+x22=(x1+x2)2-2x1x2;
(2)(x1-x2)2=(x1+x2)2-4x1x2;
(3)(x1+1)(x2+1)=x1x2+(x1+x2)+1;
