人教版八年级数学下册(第十九章一次函数19.2~19.3)基础知识整理与复习训练(附图片答案)
文档属性
| 名称 | 人教版八年级数学下册(第十九章一次函数19.2~19.3)基础知识整理与复习训练(附图片答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-18 00:00:00 | ||
图片预览


文档简介
? 人教版八年级数学(第十九章19.2~19.3)基础知识整理与复习训练
知识要点一 一次函数与一元一次方程
1.若一次函数y=kx+b的图象如图所示,则方程x+b=0的解为( )
A .x=2 B.y=2 C.x=-1 D.y=-1
2.若一次函数y=kx+b(k,b为常数,且k≠0)x与y的部分对应值如下表,则方程kx+b=0的解是( )
x -1 0 1 2
y 2 1 0 -1
x=0 B.x=-1 C=1 D.x=2
3.次函数y=-3x+6的图象与y轴的交点坐标是__________.
4.已知关于x的方程mx+n=0的解是x=-1,则直线y=mx+n与x轴的交点坐标
是__________.
5.某种收割机开始工作时,油箱中有24升油,如果每小时耗油4升,那么油箱中剩余的油量y(升)与工作时间x(时)之间的函数解析式为__________,当油箱中剩余12升油时,收割机工作了__________小时.
6.在直线y=-x+3上分别找出满足下列条件的点,并写出它的坐标.
(1)横坐标是-4的点;
(2)函数值为0的点;
(3)到x轴的距离是2个单位长度的点.
知识要点二 一次函数与ー元一次不等式
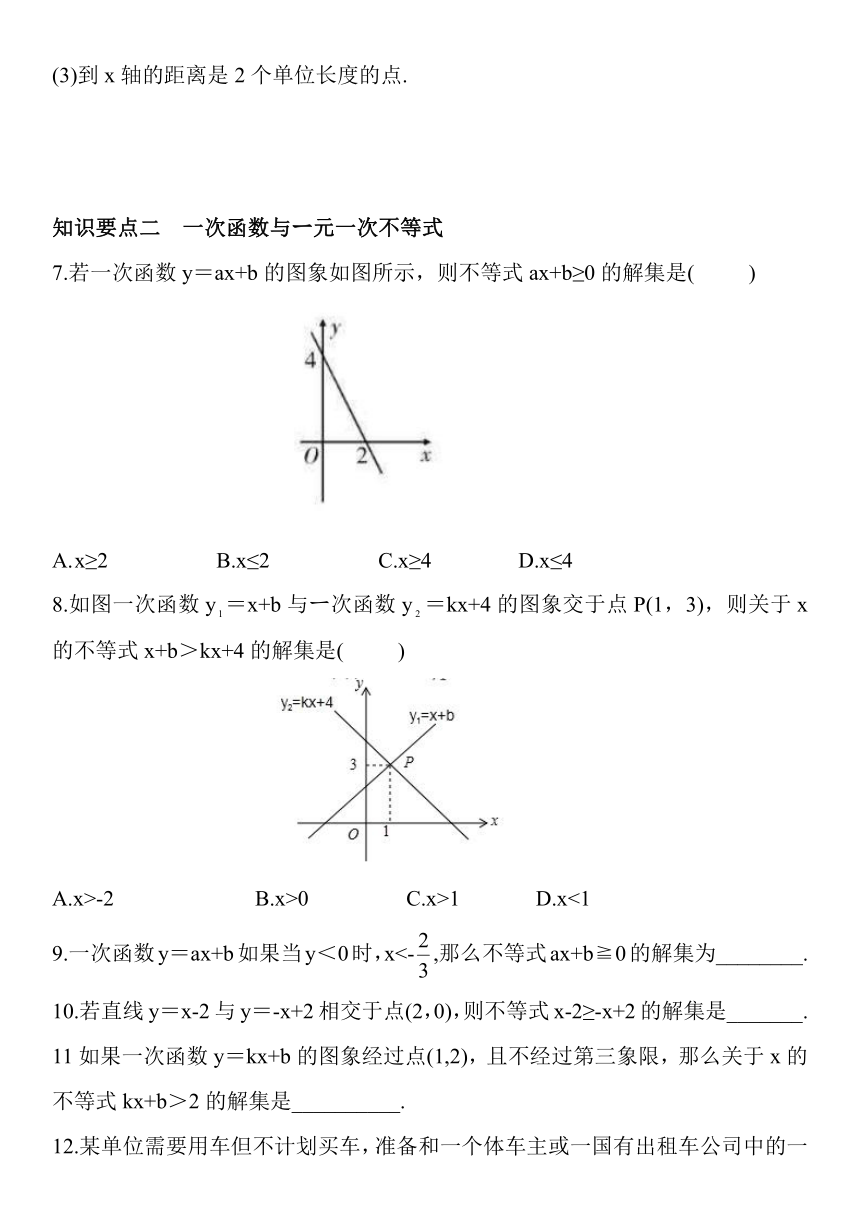
7.若一次函数y=ax+b的图象如图所示,则不等式ax+b≥0的解集是( )
x≥2 B.x≤2 C.x≥4 D.x≤4
8.如图一次函数y=x+b与ー次函数y=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )
A.x>-2 B.x>0 C.x>1 D.x<1
9.一次函数y=ax+b如果当y<0时,x<-,那么不等式ax+b≧0的解集为________.
10.若直线y=x-2与y=-x+2相交于点(2,0),则不等式x-2≥-x+2的解集是_______.
11如果一次函数y=kx+b的图象经过点(1,2),且不经过第三象限,那么关于x的不等式kx+b>2的解集是__________.
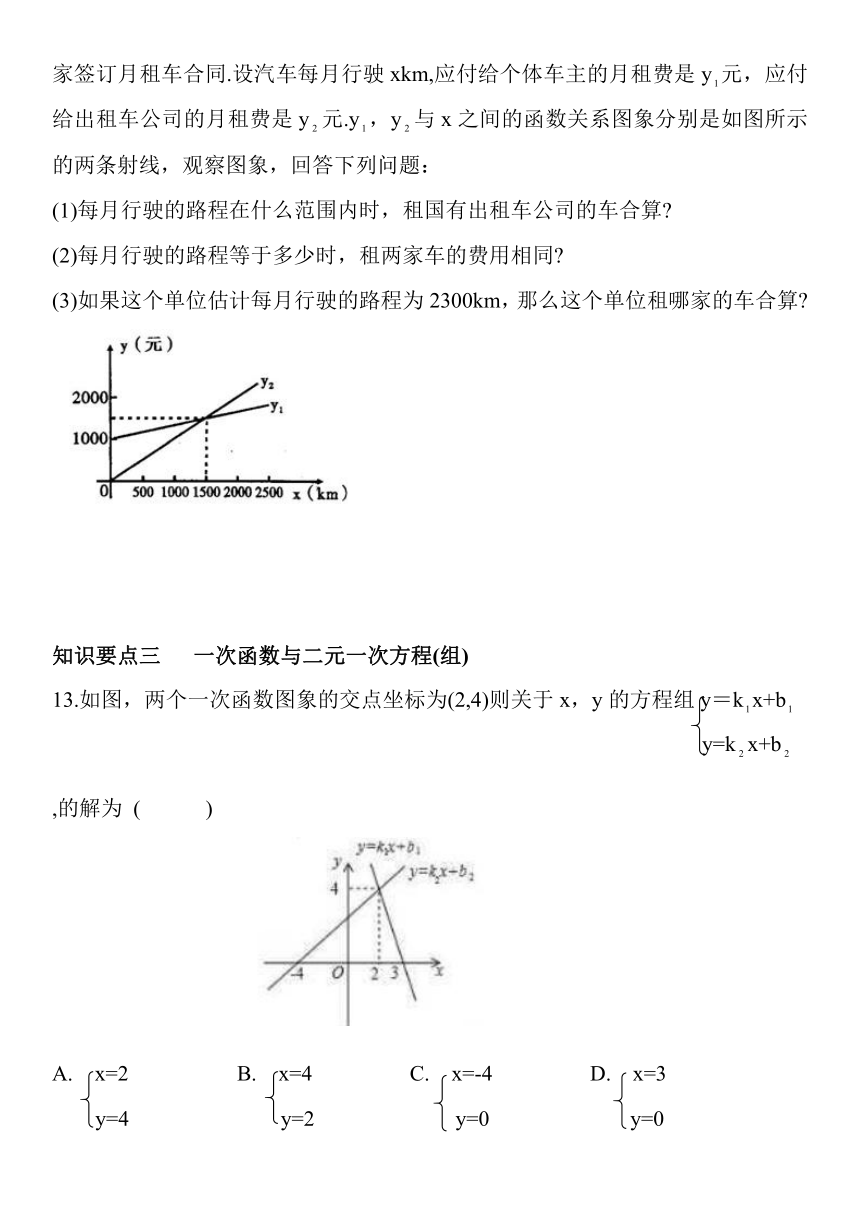
12.某单位需要用车但不计划买车,准备和一个体车主或一国有出租车公司中的一家签订月租车合同.设汽车每月行驶xkm,应付给个体车主的月租费是y元,应付给出租车公司的月租费是y元.y,y与x之间的函数关系图象分别是如图所示的两条射线,观察图象,回答下列问题:
(1)每月行驶的路程在什么范围内时,租国有出租车公司的车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
知识要点三 一次函数与二元一次方程(组)
13.如图,两个一次函数图象的交点坐标为(2,4)则关于x,y的方程组y=kx+b
y=kx+b
,的解为 ( )
x=2 B. x=4 C. x=-4 D. x=3
y=4 y=2 y=0 y=0
14.已知两直线y=-x+6和y=x-2,它们与x轴所围成的三角形的面积为( )
A.6 B.4 C.12 D.24
15.观察图象,方程组2x+y=8的解为_________.
x+y=5
16.如果方程组 y=-x+1无解,那么直线y=(-k+1)x-3不经过第_______象限.
y=(2k+1)x-3
17.在平面直角坐标系中,直线经过点(2,3)和(-1,-3),直线经过原点O,且与直线交于点P(-2,a).
(1)求a的值.
(2) x=-2可看成怎样的二元一次方程组的解?
y=a
设直线与y轴交于点A,你能求出△APO的面积吗?
?
18.已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分別表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B晚出发几小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
知识要点四 选择方案
19.如图所示,购买一种苹果,所付金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )
A.1元 B.2元 C.3元 D.4元
20.学校需要添置A,B两种型号的教师办公桌椅共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两种型号桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,每套桌椅需要运费10元,设购买A型桌椅x套时,总费用为y元,求y与x的函数解析式,并直接写出x的取值范围:
(3)在(2)的条件下,求出总费用最少的购置方案.
参考答案
知识要点一 一次函数与一元一次方程
1.若一次函数y=kx+b的图象如图所示,则方程x+b=0的解为( )
A .x=2 B.y=2 C.x=-1 D.y=-1
2.若一次函数y=kx+b(k,b为常数,且k≠0)x与y的部分对应值如下表,则方程kx+b=0的解是( )
x -1 0 1 2
y 2 1 0 -1
x=0 B.x=-1 C=1 D.x=2
3.次函数y=-3x+6的图象与y轴的交点坐标是__________.
4.已知关于x的方程mx+n=0的解是x=-1,则直线y=mx+n与x轴的交点坐标
是__________.
5.某种收割机开始工作时,油箱中有24升油,如果每小时耗油4升,那么油箱中剩余的油量y(升)与工作时间x(时)之间的函数解析式为__________,当油箱中剩余12升油时,收割机工作了__________小时.
6.在直线y=-x+3上分别找出满足下列条件的点,并写出它的坐标.
(1)横坐标是-4的点;
(2)函数值为0的点;
(3)到x轴的距离是2个单位长度的点.
知识要点二 一次函数与ー元一次不等式
7.若一次函数y=ax+b的图象如图所示,则不等式ax+b≥0的解集是( )
x≥2 B.x≤2 C.x≥4 D.x≤4
8.如图一次函数y=x+b与ー次函数y=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )
A.x>-2 B.x>0 C.x>1 D.x<1
9.一次函数y=ax+b如果当y<0时,x<-,那么不等式ax+b≧0的解集为________.
10.若直线y=x-2与y=-x+2相交于点(2,0),则不等式x-2≥-x+2的解集是_______.
11如果一次函数y=kx+b的图象经过点(1,2),且不经过第三象限,那么关于x的不等式kx+b>2的解集是__________.
12.某单位需要用车但不计划买车,准备和一个体车主或一国有出租车公司中的一家签订月租车合同.设汽车每月行驶xkm,应付给个体车主的月租费是y元,应付给出租车公司的月租费是y元.y,y与x之间的函数关系图象分别是如图所示的两条射线,观察图象,回答下列问题:
(1)每月行驶的路程在什么范围内时,租国有出租车公司的车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
知识要点三 一次函数与二元一次方程(组)
13.如图,两个一次函数图象的交点坐标为(2,4)则关于x,y的方程组y=kx+b
y=kx+b
,的解为 ( )
x=2 B. x=4 C. x=-4 D. x=3
y=4 y=2 y=0 y=0
14.已知两直线y=-x+6和y=x-2,它们与x轴所围成的三角形的面积为( )
A.6 B.4 C.12 D.24
15.观察图象,方程组2x+y=8的解为_________.
x+y=5
16.如果方程组 y=-x+1无解,那么直线y=(-k+1)x-3不经过第_______象限.
y=(2k+1)x-3
17.在平面直角坐标系中,直线经过点(2,3)和(-1,-3),直线经过原点O,且与直线交于点P(-2,a).
(1)求a的值.
(2) x=-2可看成怎样的二元一次方程组的解?
y=a
设直线与y轴交于点A,你能求出△APO的面积吗?
?
18.已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分別表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B晚出发几小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
知识要点四 选择方案
19.如图所示,购买一种苹果,所付金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )
A.1元 B.2元 C.3元 D.4元
20.学校需要添置A,B两种型号的教师办公桌椅共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两种型号桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,每套桌椅需要运费10元,设购买A型桌椅x套时,总费用为y元,求y与x的函数解析式,并直接写出x的取值范围:
(3)在(2)的条件下,求出总费用最少的购置方案.
参考答案
