九年级数学下册第26章二次函数阶段专题复习习题课件华东师大版(72张)
文档属性
| 名称 | 九年级数学下册第26章二次函数阶段专题复习习题课件华东师大版(72张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 00:00:00 | ||
图片预览










文档简介
(共72张PPT)
阶段专题复习
第 27 章
请写出框图中数字处的内容:
①___________________________________________________;
②______________________________;
③_________________;
④______________________________;
⑤___________; ⑥___________;
⑦__________________;⑧___________;
⑨___________;⑩_________.
形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数
y=ax2+bx+c=0(a,b,c是常数,a≠0)
列表、描点、连线
a>0时,开口向上,a<0时,开口向下
上加下减,左加右减
有两个交点
有一个交点
没有交点
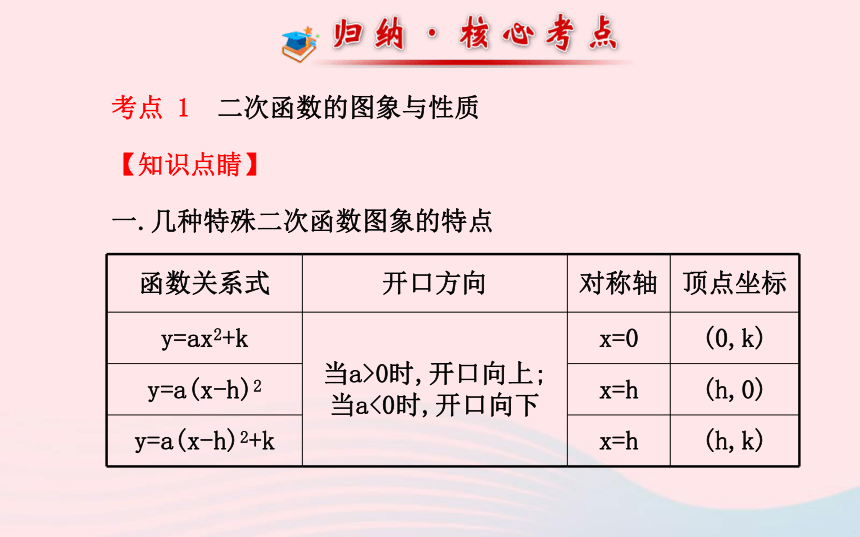
考点 1 二次函数的图象与性质
【知识点睛】
一.几种特殊二次函数图象的特点
函数关系式 开口方向 对称轴 顶点坐标
y=ax2+k 当a>0时,开口向上;当a<0时,开口向下 x=0 (0,k)
y=a(x-h)2 x=h (h,0)
y=a(x-h)2+k x=h (h,k)
二.确定二次函数的对称轴和顶点坐标的方法
1.公式法:对称轴是直线 顶点坐标是
2.配方法:将二次函数通过配方化为y=a(x-h)2+k(a≠0)的
形式,对称轴为x=h,顶点坐标是(h,k).
【例1】(河北中考)如图,抛物线y1=a(x+2)2-3与
交于点A(1,3),过点A作x轴的平行线,分
别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2
的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=
3AC.其中正确的结论是( )
A.①② B.②③ C.③④ D.①④
【思路点拨】 根据 的图象在x轴上方即可得出
y2的取值范围;把A(1,3)代入抛物线 即可
得出a的值;由抛物线与y轴的交点求出y2-y1的值;根据两函
数的关系式直接得出AB与AC的关系即可.
【自主解答】选D.由图象可以知道y2的图象全部在x轴上方,
所以无论x取何值,y2的值总是正数.∵抛物线y1=a(x+2)2-
3过点A(1,3),∴a(1+2)2-3=3, 即
当x=0时, 则 当y=3时,
=3,解得x=-5或x=1,即A(1,3),B(-5,3),则AB=6;
当y=3时, 解得x=5或x=1,即A(1,3),C(5,
3),则AC=4,∴2AB=3AC.因此,其中正确的有①④.
【中考集训】
1.(菏泽中考)已知b<0时,二次函数y=ax2+bx+a2
-1的图象如下列四个图之一所示.根据图象分析,a的值等
于( )
A.-2 B.-1 C.1 D.2
【解析】选C.由图可知,第1,2两个图形的对称轴为y轴,所
以
解得b=0,与b<0相矛盾;第3个图,抛物线开口向上,a>0,
经过坐标原点,a2-1=0,解得a1=1,a2=-1(舍去),对称轴
所以b<0,符合题意,故a=1;第4个图,抛
物线开口向下,a<0,经过坐标原点,a2-1=0,解得a1=1(舍
去),a2=-1,对称轴 所以b>0,不符合
题意,综上所述,a的值等于1.
2.(恩施中考)把抛物线 先向右平移1个单
位,再向下平移2个单位,得到的抛物线的关系式为( )
【解析】选B.根据抛物线平移规律“左加右减,上加下减”可
得B项正确.
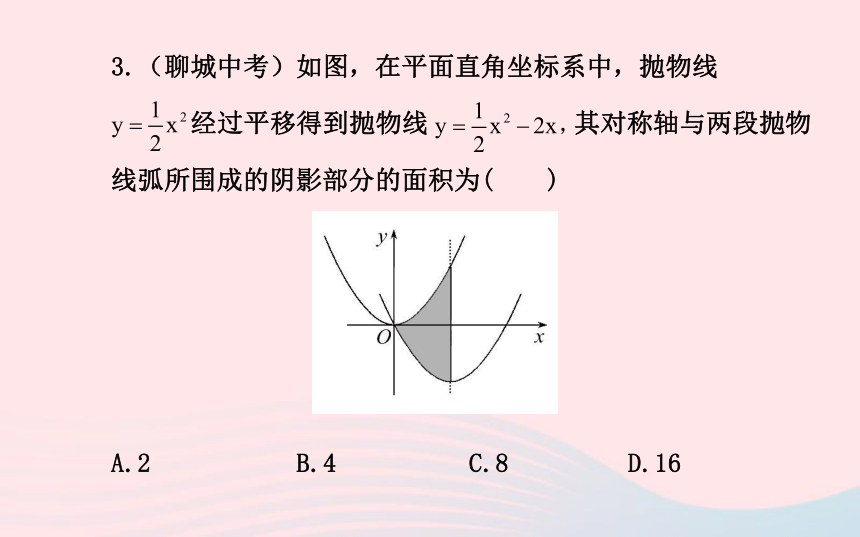
3.(聊城中考)如图,在平面直角坐标系中,抛物线
经过平移得到抛物线 其对称轴与两段抛物
线弧所围成的阴影部分的面积为( )
A.2 B.4 C.8 D.16
【解析】选B.依据平移的定义及抛物线的对称性可得:区域D的面积=区域C的面积=区域B的面积,∴待求阴影面积=区域A的面积加上区域D的面积=正方形的面积=4.
4.(牡丹江中考)若抛物线y=ax2+bx+c经过点(-1,10),则a-b+c=________.
【解析】y=ax2+bx+c经过点(-1,10),则点的坐标(-1,10)就符合y=ax2+bx+c,代入得,a-b+c=10.
答案:10
5.(杭州中考)已知抛物线y1=ax2+bx+c(a≠0)与x轴相交
于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次
函数 的图象上,线段AB长为16,线段OC长为8,当y1随
着x的增大而减小时,求自变量x的取值范围.
【解析】根据OC长为8可得一次函数中的n的值为8或-8,
分类讨论:(1)n=8时,易得A(-6,0),如图,
∵抛物线过A,C两点,且与x轴交点A,B在原点两侧,
∴抛物线开口向下,则a<0.
∵AB=16,且A(-6,0),
∴B(10,0),而A,B关于对称轴对称,
∴对称轴直线
要使y1随着x的增大而减小,且a<0,
∴x>2.
(2)n=-8时,易得A(6,0),如图,
∵抛物线过A,C两点,且与x轴交点A,B在原点两侧,
∴抛物线开口向上,则a>0.
∵AB=16,且A(6,0),
∴B(-10,0),而A,B关于对称轴对称,
∴对称轴直线
要使y1随着x的增大而减小,且a>0,∴x<-2.
考点 2 确定函数关系式
【知识点睛】
待定系数法主要用于确定二次函数的关系式
1.当已知抛物线上任意三点坐标时,可以通过设函数关系式为一般式y=ax2+bx+c(a≠0)进行求解.
2.当已知抛物线顶点坐标、对称轴或最值时,可以通过设函数关系式为y=a(x-h)2+k(a≠0)进行求解.
3.如果已知抛物线与x轴的两个交点(x1,0)(x2,0)时,可设为交点式y=a(x-x1)(x-x2)进行求解.
【例2】(安徽中考)已知二次函数图象的顶点坐标为
(1,-1),且过原点(0,0),求该函数关系式.
【思路点拨】已知顶点坐标,可设为顶点式,再将(0,0)代入,
求出函数关系式.
【自主解答】∵二次函数图象的顶点坐标为(1,-1),
∴设为y=a(x-1)2-1,当x=0时,y=0,
∴0=a(0-1)2-1,a=1,
所求函数关系式为y=(x-1)2-1.
【中考集训】
1.(厦门中考)已知两个变量x和y,它们之间的3组对应值
如下表所示.
则y与x之间的函数关系式可能是( )
A.y=x B.y=2x+1
C.y=x2+x+1 D.
x -1 0 1
y -1 1 3
【解析】选B.A.y=x,当x=0时,y=0,此时与表格不符合,故
此选项错误;
B.y=2x+1,根据表格对应数据代入得出y=2x+1,故此选项正
确;
C.y=x2+x+1,当x=-1时,y=x2+x+1=1≠-1,故此选项错误;
D. 中x≠0,故此选项错误.
2.(广元中考)若二次函数y=ax2+bx+a2-2(a,b为常
数)的图象如图,则a的值为( )
【解析】选C.∵图象经过原点,∴a2-2=0,得: 或
∵图象开口向下,
3.(嘉兴中考)如图,已知二次函数y=x2+bx+c的图象
经过点(-1,0),(1,-2),当y随x的增大而增大时,x的
取值范围是________.
【解析】 把(-1,0),(1,-2)代入二次函数y=x2+bx+c
中,得
那么二次函数的关系式是y=x2-x-2.
函数的对称轴是:
因而当y随x的增大而增大时,x的取值范围是:
答案:
4.(丽水中考)如图,已知抛物线 与直线
y=2x交于点O(0,0),A(a,12),点B是抛物线上O,A之间
的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点
C,E.
(1)求抛物线的函数关系式.
(2)若点C为OA的中点,求BC的长.
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
【解析】(1)∵点A(a,12)在直线y=2x上,
∴12=2a,即a=6,
∴点A的坐标为(6,12).
又∵点A是抛物线 上的一点,
把A(6,12)代入 得b=-1.
∴抛物线的函数关系式为
(2)∵点C为OA的中点,∴点C的坐标为(3,6).
把y=6代入
解得 (舍去),
(3)∵点D的坐标为(m,n),
∴点E的坐标为 点C的坐标为(m,2m).
∴点B的坐标为
把 代入
可得
∴m,n之间的关系式为
考点 3 二次函数图象与a,b,c的关系
【知识点睛】
系数的符号 图象特征
a的符号 开口向上?a>0,开口向下?a<0
b的符号 左同右异,顶点在y轴左侧,b与a符号相同;顶点在y轴右侧,b与a符号相异
c的符号 c为图象与y轴交点的纵坐标
某些特殊形式的代数式的符号的判断:
(1)a+b+c,即x=1时y的值.
(2)b2-4ac,根据图象与x轴交点的个数判断.
【例3】(玉林中考)二次函数y=ax2+bx+c(a≠0)的图象
如图所示,其对称轴为直线x=1,有如下结论:
①c<1;②2a+b=0;③b2<4ac;④若方程ax2+bx+c=0的两根为x1,x2,
则x1+x2=2.则正确的结论是( )
A.①② B.①③ C.②④ D.③④
【思路点拨】由抛物线与y轴的交点在1的上方,得到c的取值范围;由抛物线的对称轴为x=1,利用对称轴公式得到关于a与b的关系;由抛物线与x轴的交点有两个,得到根的判别式大于0,整理可判断③;令抛物线关系式中y=0,得到关于x的一元二次方程,利用根与系数的关系表示出两根之和,将得到的a与b的关系式代入可得出两根之和.
【自主解答】选C.由抛物线与y轴的交点位置得到:c>1,
①错误;
∵抛物线的对称轴为
∴2a+b=0,②正确;
由抛物线与x轴有两个交点,得到b2-4ac>0,即b2>4ac,
③错误;
令抛物线关系式中y=0,得到ax2+bx+c=0,
∵方程的两根为x1,x2,且
④正确,
综上,正确的结论有②④.
【中考集训】
1.(鞍山中考)如图所示的抛物线是二次函数y=
ax2+bx+c(a≠0)的图象,则下列结论:①abc>0;②b+
2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;
⑤3a+c<0.其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
【解析】选B.∵开口向上,∴a>0,
∵与y轴交于负半轴,
∴c<0,∵对称轴
∴b<0,∴abc>0,故①正确;
∵对称轴
∴b+2a=0,故②正确;
∵抛物线与x轴的一个交点为(-2,0),对称轴为x=1,
∴抛物线与x轴的另一个交点为(4,0),故③正确;
∵当x=-1时,y=a-b+c<0,
∴a+c<b,故④错误;∵a-b+c<0,b+2a=0,
∴3a+c<0,故⑤正确.故选B.
2.(济南中考)如图,二次函数y=ax2+bx+c的图象经过点
(1,-2),与x轴交点的横坐标分别为x1,x2,且-1<x1<0,
1<x2<2,下列结论正确的是( )
A.a<0 B.a-b+c<0
C. D.4ac-b2<-8a
【解析】选D.根据图象可知:
(1)a>0.(2)x=-1对应的函数值a-b+c>0.(3)对称轴在0和1
之间,因此 (4)函数的最小值小于-2,因此
<-2,即4ac-b2<-8a.
3.(济宁中考)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
A.a>0
B.当-10
C.c<0
D.当x≥1时,y随x的增大而增大
【解析】选B.∵开口向下,
∴a<0,即A不正确;
由二次函数的图象的对称性可知,
图象与x轴的另一个交点的横坐标为3,
由图象看出,当-1即y>0,∴B正确;
∵图象与y轴交点在y轴正半轴上,∴c>0,即C不正确;
∵图象开口向下,对称轴是x=1,
∴当x≥1时,y随x的增大而减小,即D不正确.
4.(潜江中考)已知二次函数y=ax2+bx+c的图象如图所示,
它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-
2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
【解析】选B.根据图象可得:a>0,c<0,
对称轴:
①∵它与x轴的两个交点分别为(-1,0),(3,0),
∴对称轴是x=1,
∴b+2a=0,故①错误;
②∵a>0,∴b<0,
∴abc>0,故②错误;
③∵b+2a=0,
∴a-2b+4c=a+2b-4b+4c=-4b+4c,
∵a-b+c=0,
∴4a-4b+4c=0,
∴-4b+4c=-4a,
∵a>0,∴a-2b+4c=-4b+4c=-4a<0,故③正确;
④根据图示知,当x=4时,y>0,
∴16a+4b+c>0,由①知,b=-2a,
∴8a+c>0,故④正确.
所以正确的为:③④两个.
考点 4 二次函数图象与a,b,c的关系
【知识点睛】
在应用二次函数解决实际问题时,首先要注意对实际问题进行观察分析,并从中抽象出相应的数量关系,建立二次函数模型,进而利用二次函数的图象与性质解答.在解答时要注意实际问题中数量及数量关系的意义要符合实际问题的要求和限制,特别是自变量取值范围的限制及其对应的函数值的取值范围的要求.
【例4】(安徽中考)某大学生利用暑假40天社会实践参与了一家网店的经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示.
销售量p(件) p=50-x
销售单价q(元/件) 当1≤x≤20时,
当21≤x≤40时,
(1)请计算第几天该商品的销售单价为35元/件.
(2)求该网店第x天获得的利润y关于x的函数关系式.
(3)这40天中该网店第几天获得的利润最大?最大利润是多少?
【思路点拨】(1)本小题是已知函数值求自变量的取值,一般采用代入法,由于销售单价q是关于第x天的分段函数,因此要分两种情况代入求值,并检验x的取值是否在每段取值范围内.
(2)根据“利润=每件商品的销售利润×销售的件数”建立函数关系式,这也是一个分段函数.
(3)分两种情况:当获得的利润y是x的二次函数关系时,利用配方法配成顶点形式,结合自变量取值范围求出函数最大值;当获得的利润y是x的非二次函数时,结合自变量x的取值范围求出函数最大值,并综合考虑求出该网店第几天获得的利润最大.
【自主解答】(1)①对于 当q=35时,
解得x=10在1≤x≤20范围内;②对于 当q=35时,
解得x=35在21≤x≤40范围内.综上所述,第10天
或第35天该商品的销售单价为35元/件.
(2)①当1≤x≤20时,
②当21≤x≤40时,
(3)① 由于 抛
物线开口向下,且1≤x≤20,所以当x=15时,y最大=612.5
(元);
② 越大(即x越小)y的值越大,由于
21≤x≤40,
所以当x=21时,y最大=1 250-525=725(元),
综上所述,这40天中该网店第21天获得的利润最大,最大利润
是725元.
【中考集训】
1.(嘉兴中考)某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出x辆时,日收益为y元.(日收益=日租金收入-平均每日各项支出)
(1)公司每日租出x辆时,每辆车的日租金为________元(用含x的代数式表示).
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司日收益不盈也不亏?
【解析】(1)1400-50x
(2)y=x(-50x+1400)-4800=-50x2+1400x-4800=-50(x-14)2+
5000(0≤x≤20).
∴当x=14时,y有最大值5000.
∴当每日租出14辆时,租赁公司日收益最大,最大值为5000元.
(3)要使租赁公司日收益不盈也不亏,即y=0.
即-50(x-14)2+5000=0,
解得x1=24,x2=4.
∵x=24不合题意,舍去.
∴当每日租出4辆时,租赁公司日收益不盈也不亏.
2.(无锡中考)如图,在边长为24 cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A,B,C,D四个顶点正好重合于上底面上一点).已知E,F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x cm.
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V.
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
【解析】(1)根据题意,知这个正方体的底面边长 则
EF=2x,∴x+2x+x=24,x=6(cm).
(2)设包装盒的底面边长为a cm,高为h cm,
则
=-6x2+96x=-6(x-8)2+384,
∵03.(长沙中考)在长株潭建设两型社会的过程中,为推
进节能减排,发展低碳经济,我市某公司以25万元购得某项节
能产品的生产技术后,再投入100万元购买生产设备,进行该
产品的生产加工.已知生产这种产品的成本价为每件20元.经过
市场调研发现,该产品的销售单价定在25元到35元之间较为合
理,并且该产品的年销售量y(万件)与销售单价x(元)之间
的函数关系式为:
(年获利=年销售收入-生产成本-投资成本)
(1)当销售单价定为28元时,该产品的年销售量为多少万件?
(2)求该公司第一年的年获利W(万元)与销售单价x(元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(3)第二年,该公司决定给希望工程捐款Z万元,该项捐款由两部分组成:一部分为10万元的固定捐款;另一部分则为每销售一件产品,就抽出一元钱作为捐款.若除去第一年的最大获利(或最小亏损)以及第二年的捐款后,到第二年年底,两年的总盈利不低于67.5万元,请你确定此时销售单价的范围.
【解析】(1)当x=28时,y=40-28=12.
答:产品的年销售量为12万件.
(2)①当25≤x≤30时,W=(40-x)(x-20)-25-100=-x2+60x-925
=-(x-30)2-25,
故当x=30时,W最大为-25,
即公司最少亏损25万元;
②当30
故当x=35时,W最大为-12.5,
即公司最少亏损12.5万元;
综上所述,投资的第一年,公司亏损,最少亏损12.5万元.
(3)①当25≤x≤30时,
W=(40-x)(x-20-1)-12.5-10
=-x2+61x-862.5,
令W=67.5,则-x2+61x-862.5=67.5,化简得:x2-61x+930=0,
x1=31,x2=30,即当两年的总盈利不低于67.5万元时,x=30;
②当30
令W=67.5,则 化简得:x2-71x+1 230
=0,x1=30,x2=41,即当两年的总盈利不低于67.5万元时,
30综上所述,到第二年年底,两年的总盈利不低于67.5万元时,
销售单价的范围是30≤x≤35.
4.(聊城中考)某电子厂商投产一种新型电子产品,每
件制造成本为18元,试销过程中发现,每月销售量y(万件)
与销售单价x(元)之间的关系可以近似地看作一次函数y=
-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函
数关系式.
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
【解析】(1)z=(x-18)y=(x-18)(-2x+100)=-2x2+136x-1800,
∴z与x之间的函数关系式为z=-2x2+136x-1800.
(2)由z=350,得350=-2x2+136x-1800,解这个方程得x1=25,x2=43.
所以,当销售单价定为25元或43元时,厂商每月能获得350万元
的利润.
z=-2x2+136x-1800=-2(x-34)2+512,
因此,当销售单价为34元时,每月能获得最大利润,最大利润是
512万元.
(3)结合(2)及函数z=-2x2+136x-1 800的图象(如图所示)可知,
当25≤x≤43时z≥350,
又由限价32元,得25≤x≤32,
根据一次函数的性质,得y=-2x+100中y随x的增大而减小,
∴当x=32时,每月制造成本最低.最低成本是18×(-2×32
+100)=648(万元),
因此,所求每月最低制造成本为648万元.
阶段专题复习
第 27 章
请写出框图中数字处的内容:
①___________________________________________________;
②______________________________;
③_________________;
④______________________________;
⑤___________; ⑥___________;
⑦__________________;⑧___________;
⑨___________;⑩_________.
形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数
y=ax2+bx+c=0(a,b,c是常数,a≠0)
列表、描点、连线
a>0时,开口向上,a<0时,开口向下
上加下减,左加右减
有两个交点
有一个交点
没有交点
考点 1 二次函数的图象与性质
【知识点睛】
一.几种特殊二次函数图象的特点
函数关系式 开口方向 对称轴 顶点坐标
y=ax2+k 当a>0时,开口向上;当a<0时,开口向下 x=0 (0,k)
y=a(x-h)2 x=h (h,0)
y=a(x-h)2+k x=h (h,k)
二.确定二次函数的对称轴和顶点坐标的方法
1.公式法:对称轴是直线 顶点坐标是
2.配方法:将二次函数通过配方化为y=a(x-h)2+k(a≠0)的
形式,对称轴为x=h,顶点坐标是(h,k).
【例1】(河北中考)如图,抛物线y1=a(x+2)2-3与
交于点A(1,3),过点A作x轴的平行线,分
别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2
的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=
3AC.其中正确的结论是( )
A.①② B.②③ C.③④ D.①④
【思路点拨】 根据 的图象在x轴上方即可得出
y2的取值范围;把A(1,3)代入抛物线 即可
得出a的值;由抛物线与y轴的交点求出y2-y1的值;根据两函
数的关系式直接得出AB与AC的关系即可.
【自主解答】选D.由图象可以知道y2的图象全部在x轴上方,
所以无论x取何值,y2的值总是正数.∵抛物线y1=a(x+2)2-
3过点A(1,3),∴a(1+2)2-3=3, 即
当x=0时, 则 当y=3时,
=3,解得x=-5或x=1,即A(1,3),B(-5,3),则AB=6;
当y=3时, 解得x=5或x=1,即A(1,3),C(5,
3),则AC=4,∴2AB=3AC.因此,其中正确的有①④.
【中考集训】
1.(菏泽中考)已知b<0时,二次函数y=ax2+bx+a2
-1的图象如下列四个图之一所示.根据图象分析,a的值等
于( )
A.-2 B.-1 C.1 D.2
【解析】选C.由图可知,第1,2两个图形的对称轴为y轴,所
以
解得b=0,与b<0相矛盾;第3个图,抛物线开口向上,a>0,
经过坐标原点,a2-1=0,解得a1=1,a2=-1(舍去),对称轴
所以b<0,符合题意,故a=1;第4个图,抛
物线开口向下,a<0,经过坐标原点,a2-1=0,解得a1=1(舍
去),a2=-1,对称轴 所以b>0,不符合
题意,综上所述,a的值等于1.
2.(恩施中考)把抛物线 先向右平移1个单
位,再向下平移2个单位,得到的抛物线的关系式为( )
【解析】选B.根据抛物线平移规律“左加右减,上加下减”可
得B项正确.
3.(聊城中考)如图,在平面直角坐标系中,抛物线
经过平移得到抛物线 其对称轴与两段抛物
线弧所围成的阴影部分的面积为( )
A.2 B.4 C.8 D.16
【解析】选B.依据平移的定义及抛物线的对称性可得:区域D的面积=区域C的面积=区域B的面积,∴待求阴影面积=区域A的面积加上区域D的面积=正方形的面积=4.
4.(牡丹江中考)若抛物线y=ax2+bx+c经过点(-1,10),则a-b+c=________.
【解析】y=ax2+bx+c经过点(-1,10),则点的坐标(-1,10)就符合y=ax2+bx+c,代入得,a-b+c=10.
答案:10
5.(杭州中考)已知抛物线y1=ax2+bx+c(a≠0)与x轴相交
于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次
函数 的图象上,线段AB长为16,线段OC长为8,当y1随
着x的增大而减小时,求自变量x的取值范围.
【解析】根据OC长为8可得一次函数中的n的值为8或-8,
分类讨论:(1)n=8时,易得A(-6,0),如图,
∵抛物线过A,C两点,且与x轴交点A,B在原点两侧,
∴抛物线开口向下,则a<0.
∵AB=16,且A(-6,0),
∴B(10,0),而A,B关于对称轴对称,
∴对称轴直线
要使y1随着x的增大而减小,且a<0,
∴x>2.
(2)n=-8时,易得A(6,0),如图,
∵抛物线过A,C两点,且与x轴交点A,B在原点两侧,
∴抛物线开口向上,则a>0.
∵AB=16,且A(6,0),
∴B(-10,0),而A,B关于对称轴对称,
∴对称轴直线
要使y1随着x的增大而减小,且a>0,∴x<-2.
考点 2 确定函数关系式
【知识点睛】
待定系数法主要用于确定二次函数的关系式
1.当已知抛物线上任意三点坐标时,可以通过设函数关系式为一般式y=ax2+bx+c(a≠0)进行求解.
2.当已知抛物线顶点坐标、对称轴或最值时,可以通过设函数关系式为y=a(x-h)2+k(a≠0)进行求解.
3.如果已知抛物线与x轴的两个交点(x1,0)(x2,0)时,可设为交点式y=a(x-x1)(x-x2)进行求解.
【例2】(安徽中考)已知二次函数图象的顶点坐标为
(1,-1),且过原点(0,0),求该函数关系式.
【思路点拨】已知顶点坐标,可设为顶点式,再将(0,0)代入,
求出函数关系式.
【自主解答】∵二次函数图象的顶点坐标为(1,-1),
∴设为y=a(x-1)2-1,当x=0时,y=0,
∴0=a(0-1)2-1,a=1,
所求函数关系式为y=(x-1)2-1.
【中考集训】
1.(厦门中考)已知两个变量x和y,它们之间的3组对应值
如下表所示.
则y与x之间的函数关系式可能是( )
A.y=x B.y=2x+1
C.y=x2+x+1 D.
x -1 0 1
y -1 1 3
【解析】选B.A.y=x,当x=0时,y=0,此时与表格不符合,故
此选项错误;
B.y=2x+1,根据表格对应数据代入得出y=2x+1,故此选项正
确;
C.y=x2+x+1,当x=-1时,y=x2+x+1=1≠-1,故此选项错误;
D. 中x≠0,故此选项错误.
2.(广元中考)若二次函数y=ax2+bx+a2-2(a,b为常
数)的图象如图,则a的值为( )
【解析】选C.∵图象经过原点,∴a2-2=0,得: 或
∵图象开口向下,
3.(嘉兴中考)如图,已知二次函数y=x2+bx+c的图象
经过点(-1,0),(1,-2),当y随x的增大而增大时,x的
取值范围是________.
【解析】 把(-1,0),(1,-2)代入二次函数y=x2+bx+c
中,得
那么二次函数的关系式是y=x2-x-2.
函数的对称轴是:
因而当y随x的增大而增大时,x的取值范围是:
答案:
4.(丽水中考)如图,已知抛物线 与直线
y=2x交于点O(0,0),A(a,12),点B是抛物线上O,A之间
的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点
C,E.
(1)求抛物线的函数关系式.
(2)若点C为OA的中点,求BC的长.
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
【解析】(1)∵点A(a,12)在直线y=2x上,
∴12=2a,即a=6,
∴点A的坐标为(6,12).
又∵点A是抛物线 上的一点,
把A(6,12)代入 得b=-1.
∴抛物线的函数关系式为
(2)∵点C为OA的中点,∴点C的坐标为(3,6).
把y=6代入
解得 (舍去),
(3)∵点D的坐标为(m,n),
∴点E的坐标为 点C的坐标为(m,2m).
∴点B的坐标为
把 代入
可得
∴m,n之间的关系式为
考点 3 二次函数图象与a,b,c的关系
【知识点睛】
系数的符号 图象特征
a的符号 开口向上?a>0,开口向下?a<0
b的符号 左同右异,顶点在y轴左侧,b与a符号相同;顶点在y轴右侧,b与a符号相异
c的符号 c为图象与y轴交点的纵坐标
某些特殊形式的代数式的符号的判断:
(1)a+b+c,即x=1时y的值.
(2)b2-4ac,根据图象与x轴交点的个数判断.
【例3】(玉林中考)二次函数y=ax2+bx+c(a≠0)的图象
如图所示,其对称轴为直线x=1,有如下结论:
①c<1;②2a+b=0;③b2<4ac;④若方程ax2+bx+c=0的两根为x1,x2,
则x1+x2=2.则正确的结论是( )
A.①② B.①③ C.②④ D.③④
【思路点拨】由抛物线与y轴的交点在1的上方,得到c的取值范围;由抛物线的对称轴为x=1,利用对称轴公式得到关于a与b的关系;由抛物线与x轴的交点有两个,得到根的判别式大于0,整理可判断③;令抛物线关系式中y=0,得到关于x的一元二次方程,利用根与系数的关系表示出两根之和,将得到的a与b的关系式代入可得出两根之和.
【自主解答】选C.由抛物线与y轴的交点位置得到:c>1,
①错误;
∵抛物线的对称轴为
∴2a+b=0,②正确;
由抛物线与x轴有两个交点,得到b2-4ac>0,即b2>4ac,
③错误;
令抛物线关系式中y=0,得到ax2+bx+c=0,
∵方程的两根为x1,x2,且
④正确,
综上,正确的结论有②④.
【中考集训】
1.(鞍山中考)如图所示的抛物线是二次函数y=
ax2+bx+c(a≠0)的图象,则下列结论:①abc>0;②b+
2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;
⑤3a+c<0.其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
【解析】选B.∵开口向上,∴a>0,
∵与y轴交于负半轴,
∴c<0,∵对称轴
∴b<0,∴abc>0,故①正确;
∵对称轴
∴b+2a=0,故②正确;
∵抛物线与x轴的一个交点为(-2,0),对称轴为x=1,
∴抛物线与x轴的另一个交点为(4,0),故③正确;
∵当x=-1时,y=a-b+c<0,
∴a+c<b,故④错误;∵a-b+c<0,b+2a=0,
∴3a+c<0,故⑤正确.故选B.
2.(济南中考)如图,二次函数y=ax2+bx+c的图象经过点
(1,-2),与x轴交点的横坐标分别为x1,x2,且-1<x1<0,
1<x2<2,下列结论正确的是( )
A.a<0 B.a-b+c<0
C. D.4ac-b2<-8a
【解析】选D.根据图象可知:
(1)a>0.(2)x=-1对应的函数值a-b+c>0.(3)对称轴在0和1
之间,因此 (4)函数的最小值小于-2,因此
<-2,即4ac-b2<-8a.
3.(济宁中考)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
A.a>0
B.当-1
C.c<0
D.当x≥1时,y随x的增大而增大
【解析】选B.∵开口向下,
∴a<0,即A不正确;
由二次函数的图象的对称性可知,
图象与x轴的另一个交点的横坐标为3,
由图象看出,当-1
∵图象与y轴交点在y轴正半轴上,∴c>0,即C不正确;
∵图象开口向下,对称轴是x=1,
∴当x≥1时,y随x的增大而减小,即D不正确.
4.(潜江中考)已知二次函数y=ax2+bx+c的图象如图所示,
它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-
2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
【解析】选B.根据图象可得:a>0,c<0,
对称轴:
①∵它与x轴的两个交点分别为(-1,0),(3,0),
∴对称轴是x=1,
∴b+2a=0,故①错误;
②∵a>0,∴b<0,
∴abc>0,故②错误;
③∵b+2a=0,
∴a-2b+4c=a+2b-4b+4c=-4b+4c,
∵a-b+c=0,
∴4a-4b+4c=0,
∴-4b+4c=-4a,
∵a>0,∴a-2b+4c=-4b+4c=-4a<0,故③正确;
④根据图示知,当x=4时,y>0,
∴16a+4b+c>0,由①知,b=-2a,
∴8a+c>0,故④正确.
所以正确的为:③④两个.
考点 4 二次函数图象与a,b,c的关系
【知识点睛】
在应用二次函数解决实际问题时,首先要注意对实际问题进行观察分析,并从中抽象出相应的数量关系,建立二次函数模型,进而利用二次函数的图象与性质解答.在解答时要注意实际问题中数量及数量关系的意义要符合实际问题的要求和限制,特别是自变量取值范围的限制及其对应的函数值的取值范围的要求.
【例4】(安徽中考)某大学生利用暑假40天社会实践参与了一家网店的经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示.
销售量p(件) p=50-x
销售单价q(元/件) 当1≤x≤20时,
当21≤x≤40时,
(1)请计算第几天该商品的销售单价为35元/件.
(2)求该网店第x天获得的利润y关于x的函数关系式.
(3)这40天中该网店第几天获得的利润最大?最大利润是多少?
【思路点拨】(1)本小题是已知函数值求自变量的取值,一般采用代入法,由于销售单价q是关于第x天的分段函数,因此要分两种情况代入求值,并检验x的取值是否在每段取值范围内.
(2)根据“利润=每件商品的销售利润×销售的件数”建立函数关系式,这也是一个分段函数.
(3)分两种情况:当获得的利润y是x的二次函数关系时,利用配方法配成顶点形式,结合自变量取值范围求出函数最大值;当获得的利润y是x的非二次函数时,结合自变量x的取值范围求出函数最大值,并综合考虑求出该网店第几天获得的利润最大.
【自主解答】(1)①对于 当q=35时,
解得x=10在1≤x≤20范围内;②对于 当q=35时,
解得x=35在21≤x≤40范围内.综上所述,第10天
或第35天该商品的销售单价为35元/件.
(2)①当1≤x≤20时,
②当21≤x≤40时,
(3)① 由于 抛
物线开口向下,且1≤x≤20,所以当x=15时,y最大=612.5
(元);
② 越大(即x越小)y的值越大,由于
21≤x≤40,
所以当x=21时,y最大=1 250-525=725(元),
综上所述,这40天中该网店第21天获得的利润最大,最大利润
是725元.
【中考集训】
1.(嘉兴中考)某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出x辆时,日收益为y元.(日收益=日租金收入-平均每日各项支出)
(1)公司每日租出x辆时,每辆车的日租金为________元(用含x的代数式表示).
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司日收益不盈也不亏?
【解析】(1)1400-50x
(2)y=x(-50x+1400)-4800=-50x2+1400x-4800=-50(x-14)2+
5000(0≤x≤20).
∴当x=14时,y有最大值5000.
∴当每日租出14辆时,租赁公司日收益最大,最大值为5000元.
(3)要使租赁公司日收益不盈也不亏,即y=0.
即-50(x-14)2+5000=0,
解得x1=24,x2=4.
∵x=24不合题意,舍去.
∴当每日租出4辆时,租赁公司日收益不盈也不亏.
2.(无锡中考)如图,在边长为24 cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A,B,C,D四个顶点正好重合于上底面上一点).已知E,F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x cm.
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V.
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
【解析】(1)根据题意,知这个正方体的底面边长 则
EF=2x,∴x+2x+x=24,x=6(cm).
(2)设包装盒的底面边长为a cm,高为h cm,
则
=-6x2+96x=-6(x-8)2+384,
∵0
进节能减排,发展低碳经济,我市某公司以25万元购得某项节
能产品的生产技术后,再投入100万元购买生产设备,进行该
产品的生产加工.已知生产这种产品的成本价为每件20元.经过
市场调研发现,该产品的销售单价定在25元到35元之间较为合
理,并且该产品的年销售量y(万件)与销售单价x(元)之间
的函数关系式为:
(年获利=年销售收入-生产成本-投资成本)
(1)当销售单价定为28元时,该产品的年销售量为多少万件?
(2)求该公司第一年的年获利W(万元)与销售单价x(元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(3)第二年,该公司决定给希望工程捐款Z万元,该项捐款由两部分组成:一部分为10万元的固定捐款;另一部分则为每销售一件产品,就抽出一元钱作为捐款.若除去第一年的最大获利(或最小亏损)以及第二年的捐款后,到第二年年底,两年的总盈利不低于67.5万元,请你确定此时销售单价的范围.
【解析】(1)当x=28时,y=40-28=12.
答:产品的年销售量为12万件.
(2)①当25≤x≤30时,W=(40-x)(x-20)-25-100=-x2+60x-925
=-(x-30)2-25,
故当x=30时,W最大为-25,
即公司最少亏损25万元;
②当30
故当x=35时,W最大为-12.5,
即公司最少亏损12.5万元;
综上所述,投资的第一年,公司亏损,最少亏损12.5万元.
(3)①当25≤x≤30时,
W=(40-x)(x-20-1)-12.5-10
=-x2+61x-862.5,
令W=67.5,则-x2+61x-862.5=67.5,化简得:x2-61x+930=0,
x1=31,x2=30,即当两年的总盈利不低于67.5万元时,x=30;
②当30
令W=67.5,则 化简得:x2-71x+1 230
=0,x1=30,x2=41,即当两年的总盈利不低于67.5万元时,
30
销售单价的范围是30≤x≤35.
4.(聊城中考)某电子厂商投产一种新型电子产品,每
件制造成本为18元,试销过程中发现,每月销售量y(万件)
与销售单价x(元)之间的关系可以近似地看作一次函数y=
-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函
数关系式.
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
【解析】(1)z=(x-18)y=(x-18)(-2x+100)=-2x2+136x-1800,
∴z与x之间的函数关系式为z=-2x2+136x-1800.
(2)由z=350,得350=-2x2+136x-1800,解这个方程得x1=25,x2=43.
所以,当销售单价定为25元或43元时,厂商每月能获得350万元
的利润.
z=-2x2+136x-1800=-2(x-34)2+512,
因此,当销售单价为34元时,每月能获得最大利润,最大利润是
512万元.
(3)结合(2)及函数z=-2x2+136x-1 800的图象(如图所示)可知,
当25≤x≤43时z≥350,
又由限价32元,得25≤x≤32,
根据一次函数的性质,得y=-2x+100中y随x的增大而减小,
∴当x=32时,每月制造成本最低.最低成本是18×(-2×32
+100)=648(万元),
因此,所求每月最低制造成本为648万元.
