九年级数学下册27.1.1圆的基本元素习题课件华东师大版(32张)
文档属性
| 名称 | 九年级数学下册27.1.1圆的基本元素习题课件华东师大版(32张) |  | |
| 格式 | zip | ||
| 文件大小 | 1011.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 15:37:38 | ||
图片预览










文档简介
(共32张PPT)
第27章 圆
§27.1 圆 的 认 识
1.圆的基本元素
1.理解并掌握圆及其基本元素弦、弧、圆心角等有关概念.(重点)
2.能够根据条件画出图形,在画图的过程中加深对圆及其基本元素的理解.(重点、难点)
一、圆的基本元素
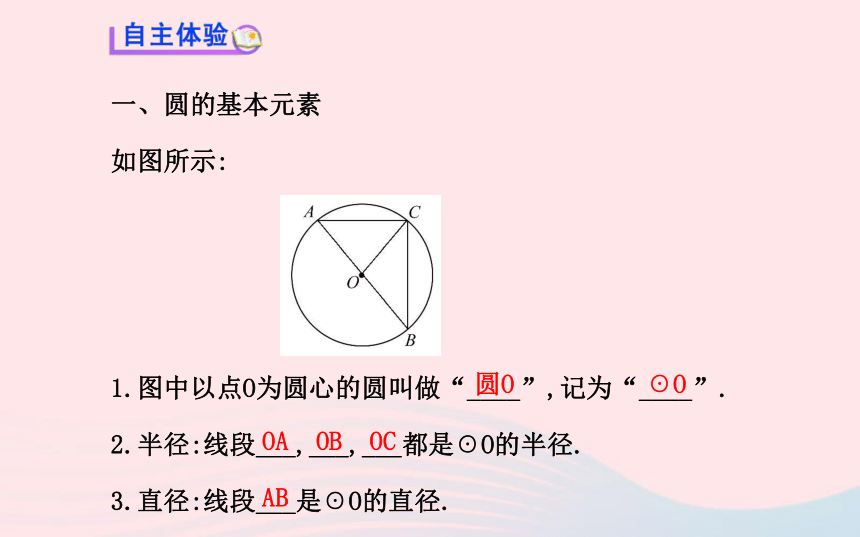
如图所示:
1.图中以点O为圆心的圆叫做“____”,记为“____”.
2.半径:线段___,___,___都是☉O的半径.
3.直径:线段___是☉O的直径.
圆O
☉O
OA
OB
OC
AB
4.弦:线段___,___,___都是⊙O中的弦.
5.弧:_____BC,AC,BAC都是⊙O中的弧,
记作___,___,____.
劣弧:_____半圆周的圆弧.___,___都是⊙O中的劣弧.
优弧:_____半圆周的圆弧.____,____都是⊙O中的优弧.
6.圆心角:______,______都是⊙O中的圆心角,____是这些
角的顶点.
AC
BC
AB
曲线
小于
大于
点O
二、圆的基本概念辨析
1.圆的位置由_____确定,圆的大小由_____长度确定,_____相
等的两个圆为等圆.
2.直径一定___弦(最长的弦),但是弦不一定___直径.
3.优弧与劣弧的不同是它们与它们所在的圆的半圆周的大小不
同,优弧_____它所在的圆的半圆周,劣弧_____它所在的圆的
半圆周;半圆既_____优弧也_____劣弧;优弧要用___个字母
表示,劣弧用___个字母表示.
圆心
半径
半径
是
是
大于
小于
不是
不是
三
两
(打“√”或“×”)
(1)⊙O半径比⊙A的半径小,所以⊙O比⊙A小 .( )
(2)优弧ABC大于劣弧AB.( )
(3)两条半径组成一条直径.( )
(4)角的顶点在圆内的角是圆心角.( )
(5)过圆心的弦是圆内最长的弦.( )
(6)长度相等的两条弧是等弧.( )
√
×
×
×
√
×
知识点 1 圆的基本元素的理解
【例1】在以下所给的命题中:①直径是弦;②弦是直径;
③半圆是弧,但弧不一定是半圆;④半径相等的两个半圆是等弧;⑤长度相等的弧是等弧.
其中正确的个数为( )
A.1 B.2 C.3 D.4
【思路点拨】根据圆中各元素的概念进行判断,要注意区分弦与直径、弧与半圆等概念.
【自主解答】选C.直径是同一个圆中最长的弦,但弦不一定是直径,所以①正确,②错误;半圆是弧,但弧不一定是半圆,如优弧和劣弧都是弧,但它们都不是半圆,所以③正确;等弧只存在等圆与同圆中,半径相等的两个圆是等圆,所以半径相等的两个半圆是等弧,长度相等的弧不一定是等弧,如果不在同圆或等圆中,即使长度相等的弧也不叫做等弧,所以④正确,⑤错误.
【总结提升】判断两段弧是等弧的两个条件
1.在同圆或等圆中.
2.能够互相重合,两者缺一不可.
知识点 2 圆的基本元素的运用
【例2】如图,⊙O的半径OA,OB分别交弦CD于点E,F,且CE=DF.请说明AE=BF.
【思路点拨】要证明AE=BF,根据圆的性质,可以转化为证明OE=OF,通过证明△OCE≌△ODF即可得出.
【自主解答】连结OC,OD,
∵OC,OD为⊙O的半径,
∴OC=OD,
∴∠OCD=∠ODC,
在△OCE和△ODF中,
∴△OCE≌△ODF(S.A.S.),
∴OE=OF.
又∵OA=OB,
∴OA-OE=OB-OF,
即AE=BF.
【总结提升】与圆的概念有关的证明和计算题两种类型
类型一:利用同圆或等圆的半径相等,借助全等三角形的知识证明线段相等或平行.
类型二:在同圆中利用半径相等,结合等腰三角形进行证明或计算.
题组一:圆的基本元素的理解
1.关于等弧的叙述正确的是( )
A.只在同圆中才会有等弧
B.只在等圆中才会有等弧
C.等弧所对应的圆的半径一定相等
D.任何两个圆中都可能存在等弧
【解析】选C.等弧存在的条件是在同圆或等圆中,所以等弧所对应的圆的半径一定相等.
2.如图,☉O中,点A,O,D,点E,D,C以及点B,O,C分别在一条直线
上,图中弦的条数有( )
A.2条 B.3条
C.4条 D.5条
【解析】选B.圆上共4个点,而连结它们的只有三条线段,所以
图中弦共有3条.
3.已知☉O中最长的弦为16cm,则☉O的半径为________cm.
【解析】∵☉O中最长的弦为16cm,即直径为16cm,
∴☉O的半径为8cm.
答案:8
4.已知☉O上一点P,以P为端点,可以画半径________条,
弦________条,直径________条.
【解析】如图所示,
过点P作半径只有一条,
为半径OP,过点P作直径
也只有一条为直径PA,
过点P的弦有无数条,如
PD,PA,PB,PC等.
答案:1 无数 1
5.如图,小虎牵着小狗上街,小虎的手臂与绳长共为2.5m(手臂与拉直的绳子在一条直线上),手臂肩部距地面1.5m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
【解析】由题意可知AB=2.5 m,AC=1.5 m,
所以 (m),
小狗活动的最大区域是以小虎的站立点为圆心,2.0 m为半径
的圆及其内部,如图.
题组二:圆的基本元素的运用
1.如图,AB为☉O的直径,点C在☉O上,若∠C=16°,则∠BOC的度数是( )
A.74° B.48°
C.32° D.16°
【解析】选C.由AO=OC,得∠A=∠C=16°,∠BOC=2∠A=32°.
2.如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长为半
径画弧,分别交直线l1,l2于B,C两点,连结AC,BC.若∠ABC=54°,
则∠1的大小为( )
A.36° B.54° C.72° D.73°
【解析】选C.如图,
∵l1∥l2,∠ABC=54°,
∴∠2=∠ABC=54°.
∵以点A为圆心,适当长为半径画
弧,分别交直线l1,l2于B,C两点,
∴AC=AB,∴∠ACB=∠ABC=54°.
∵∠1+∠ACB+∠2=180°,∴∠1=72°.
【变式备选】如图,在☉O中,P是直径AB上一动点,在AB同侧作
AA′⊥AB,BB′⊥AB,且AA′=AP,BB′=BP,连结A′B′.当点P从
点A移到点B时,A′B′的中点的位置( )
A.在平分AB的某直线上移动
B.在垂直AB的某直线上移动
C.在 上移动
D.保持固定不移动
【解析】选D.由题意知,四边形AA′B′B是直角梯形.
设A′B′的中点为D,则OD是直角梯形的中位线,即OD⊥AB.
又
故OD的长是定值,则点D是一定点,即A′B′的中点的位置保
持固定不移动.
3.在☉O中,点B在☉O上,四边形AOCB是矩形,对角线AC的长为5,
则☉O的半径长为__________.
【解析】连结OB.由四边形AOCB是矩形,得AC=OB(矩形的对角线
相等),又因为AC=5,所以OB=5,所以☉O的半径长为5.
答案:5
4.已知:如图,OA,OB为☉O的半径,C,D分别为OA,OB的中点,若AD=3厘米,则BC=______厘米.
【解析】∵OA,OB为☉O的半径,
∴OA=OB.
∵C,D分别为OA,OB的中点,
∴OD=OC,又∠AOD=∠BOC,
∴△AOD≌△BOC,
∴BC=AD=3厘米.
答案:3
5.如图,AB为☉O的直径,CD是☉O的弦,AB,CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.
【解析】连结OD,
∵AB=2DE=2OD,
∴OD=DE,又∠E=18°,
∴∠DOE=∠E=18°,
∴∠ODC=36°,
同理∠C=∠ODC=36°,
∴∠AOC=∠E+∠OCE=54°.
【想一想错在哪?】直线l经过☉O的圆心O,且与☉O交于A,B
两点,点C在☉O上,且∠AOC=30°,点P是直线l上的一个动点(与
圆心O不重合),直线CP与☉O相交于另一点Q,如果QP=QO,则
∠OCP=_______.
提示:点P是直线l上的一个动点,因而点P与线段AO有以下位置关系:点P在线段AO上,点P在OB上,点P在OA的延长线上,点P在AB的延长线上.要分这四种情况进行讨论,解题时遗漏另外三种情况,出现错误.
第27章 圆
§27.1 圆 的 认 识
1.圆的基本元素
1.理解并掌握圆及其基本元素弦、弧、圆心角等有关概念.(重点)
2.能够根据条件画出图形,在画图的过程中加深对圆及其基本元素的理解.(重点、难点)
一、圆的基本元素
如图所示:
1.图中以点O为圆心的圆叫做“____”,记为“____”.
2.半径:线段___,___,___都是☉O的半径.
3.直径:线段___是☉O的直径.
圆O
☉O
OA
OB
OC
AB
4.弦:线段___,___,___都是⊙O中的弦.
5.弧:_____BC,AC,BAC都是⊙O中的弧,
记作___,___,____.
劣弧:_____半圆周的圆弧.___,___都是⊙O中的劣弧.
优弧:_____半圆周的圆弧.____,____都是⊙O中的优弧.
6.圆心角:______,______都是⊙O中的圆心角,____是这些
角的顶点.
AC
BC
AB
曲线
小于
大于
点O
二、圆的基本概念辨析
1.圆的位置由_____确定,圆的大小由_____长度确定,_____相
等的两个圆为等圆.
2.直径一定___弦(最长的弦),但是弦不一定___直径.
3.优弧与劣弧的不同是它们与它们所在的圆的半圆周的大小不
同,优弧_____它所在的圆的半圆周,劣弧_____它所在的圆的
半圆周;半圆既_____优弧也_____劣弧;优弧要用___个字母
表示,劣弧用___个字母表示.
圆心
半径
半径
是
是
大于
小于
不是
不是
三
两
(打“√”或“×”)
(1)⊙O半径比⊙A的半径小,所以⊙O比⊙A小 .( )
(2)优弧ABC大于劣弧AB.( )
(3)两条半径组成一条直径.( )
(4)角的顶点在圆内的角是圆心角.( )
(5)过圆心的弦是圆内最长的弦.( )
(6)长度相等的两条弧是等弧.( )
√
×
×
×
√
×
知识点 1 圆的基本元素的理解
【例1】在以下所给的命题中:①直径是弦;②弦是直径;
③半圆是弧,但弧不一定是半圆;④半径相等的两个半圆是等弧;⑤长度相等的弧是等弧.
其中正确的个数为( )
A.1 B.2 C.3 D.4
【思路点拨】根据圆中各元素的概念进行判断,要注意区分弦与直径、弧与半圆等概念.
【自主解答】选C.直径是同一个圆中最长的弦,但弦不一定是直径,所以①正确,②错误;半圆是弧,但弧不一定是半圆,如优弧和劣弧都是弧,但它们都不是半圆,所以③正确;等弧只存在等圆与同圆中,半径相等的两个圆是等圆,所以半径相等的两个半圆是等弧,长度相等的弧不一定是等弧,如果不在同圆或等圆中,即使长度相等的弧也不叫做等弧,所以④正确,⑤错误.
【总结提升】判断两段弧是等弧的两个条件
1.在同圆或等圆中.
2.能够互相重合,两者缺一不可.
知识点 2 圆的基本元素的运用
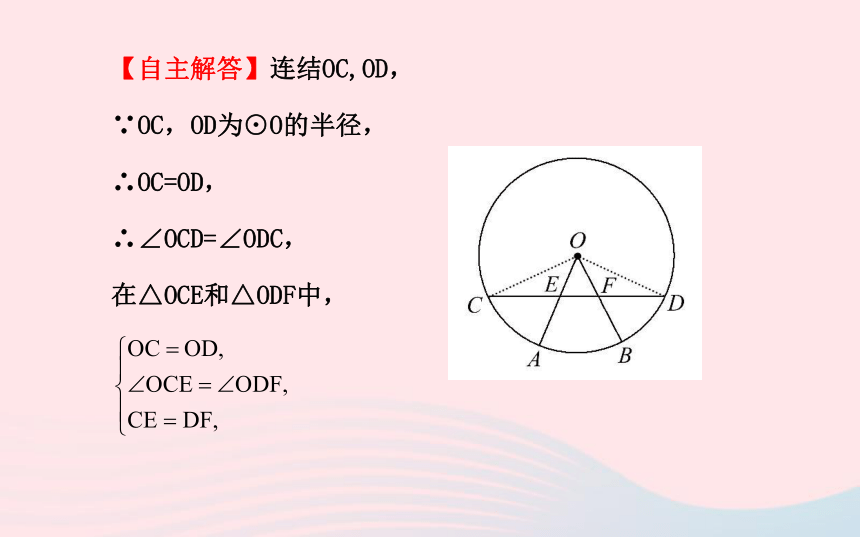
【例2】如图,⊙O的半径OA,OB分别交弦CD于点E,F,且CE=DF.请说明AE=BF.
【思路点拨】要证明AE=BF,根据圆的性质,可以转化为证明OE=OF,通过证明△OCE≌△ODF即可得出.
【自主解答】连结OC,OD,
∵OC,OD为⊙O的半径,
∴OC=OD,
∴∠OCD=∠ODC,
在△OCE和△ODF中,
∴△OCE≌△ODF(S.A.S.),
∴OE=OF.
又∵OA=OB,
∴OA-OE=OB-OF,
即AE=BF.
【总结提升】与圆的概念有关的证明和计算题两种类型
类型一:利用同圆或等圆的半径相等,借助全等三角形的知识证明线段相等或平行.
类型二:在同圆中利用半径相等,结合等腰三角形进行证明或计算.
题组一:圆的基本元素的理解
1.关于等弧的叙述正确的是( )
A.只在同圆中才会有等弧
B.只在等圆中才会有等弧
C.等弧所对应的圆的半径一定相等
D.任何两个圆中都可能存在等弧
【解析】选C.等弧存在的条件是在同圆或等圆中,所以等弧所对应的圆的半径一定相等.
2.如图,☉O中,点A,O,D,点E,D,C以及点B,O,C分别在一条直线
上,图中弦的条数有( )
A.2条 B.3条
C.4条 D.5条
【解析】选B.圆上共4个点,而连结它们的只有三条线段,所以
图中弦共有3条.
3.已知☉O中最长的弦为16cm,则☉O的半径为________cm.
【解析】∵☉O中最长的弦为16cm,即直径为16cm,
∴☉O的半径为8cm.
答案:8
4.已知☉O上一点P,以P为端点,可以画半径________条,
弦________条,直径________条.
【解析】如图所示,
过点P作半径只有一条,
为半径OP,过点P作直径
也只有一条为直径PA,
过点P的弦有无数条,如
PD,PA,PB,PC等.
答案:1 无数 1
5.如图,小虎牵着小狗上街,小虎的手臂与绳长共为2.5m(手臂与拉直的绳子在一条直线上),手臂肩部距地面1.5m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
【解析】由题意可知AB=2.5 m,AC=1.5 m,
所以 (m),
小狗活动的最大区域是以小虎的站立点为圆心,2.0 m为半径
的圆及其内部,如图.
题组二:圆的基本元素的运用
1.如图,AB为☉O的直径,点C在☉O上,若∠C=16°,则∠BOC的度数是( )
A.74° B.48°
C.32° D.16°
【解析】选C.由AO=OC,得∠A=∠C=16°,∠BOC=2∠A=32°.
2.如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长为半
径画弧,分别交直线l1,l2于B,C两点,连结AC,BC.若∠ABC=54°,
则∠1的大小为( )
A.36° B.54° C.72° D.73°
【解析】选C.如图,
∵l1∥l2,∠ABC=54°,
∴∠2=∠ABC=54°.
∵以点A为圆心,适当长为半径画
弧,分别交直线l1,l2于B,C两点,
∴AC=AB,∴∠ACB=∠ABC=54°.
∵∠1+∠ACB+∠2=180°,∴∠1=72°.
【变式备选】如图,在☉O中,P是直径AB上一动点,在AB同侧作
AA′⊥AB,BB′⊥AB,且AA′=AP,BB′=BP,连结A′B′.当点P从
点A移到点B时,A′B′的中点的位置( )
A.在平分AB的某直线上移动
B.在垂直AB的某直线上移动
C.在 上移动
D.保持固定不移动
【解析】选D.由题意知,四边形AA′B′B是直角梯形.
设A′B′的中点为D,则OD是直角梯形的中位线,即OD⊥AB.
又
故OD的长是定值,则点D是一定点,即A′B′的中点的位置保
持固定不移动.
3.在☉O中,点B在☉O上,四边形AOCB是矩形,对角线AC的长为5,
则☉O的半径长为__________.
【解析】连结OB.由四边形AOCB是矩形,得AC=OB(矩形的对角线
相等),又因为AC=5,所以OB=5,所以☉O的半径长为5.
答案:5
4.已知:如图,OA,OB为☉O的半径,C,D分别为OA,OB的中点,若AD=3厘米,则BC=______厘米.
【解析】∵OA,OB为☉O的半径,
∴OA=OB.
∵C,D分别为OA,OB的中点,
∴OD=OC,又∠AOD=∠BOC,
∴△AOD≌△BOC,
∴BC=AD=3厘米.
答案:3
5.如图,AB为☉O的直径,CD是☉O的弦,AB,CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.
【解析】连结OD,
∵AB=2DE=2OD,
∴OD=DE,又∠E=18°,
∴∠DOE=∠E=18°,
∴∠ODC=36°,
同理∠C=∠ODC=36°,
∴∠AOC=∠E+∠OCE=54°.
【想一想错在哪?】直线l经过☉O的圆心O,且与☉O交于A,B
两点,点C在☉O上,且∠AOC=30°,点P是直线l上的一个动点(与
圆心O不重合),直线CP与☉O相交于另一点Q,如果QP=QO,则
∠OCP=_______.
提示:点P是直线l上的一个动点,因而点P与线段AO有以下位置关系:点P在线段AO上,点P在OB上,点P在OA的延长线上,点P在AB的延长线上.要分这四种情况进行讨论,解题时遗漏另外三种情况,出现错误.
