九年级数学下册27.1.2圆的对称性习题课件华东师大版(38张)
文档属性
| 名称 | 九年级数学下册27.1.2圆的对称性习题课件华东师大版(38张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 15:41:06 | ||
图片预览










文档简介
(共38张PPT)
2.圆的对称性
1.理解圆的对称性.
2.掌握圆心角、弧、弦三者之间的关系,能运用它们之间的关系解决问题.(重点)
3.掌握垂径定理及其推论,能运用垂径定理及其推论解决问题.(重点、难点)
一、圆心角、弧、弦之间的关系
在同一个圆中,如果两个圆心角、两条弧、两条弦中有一组量
_____,那么它们所对应的其余各组量都分别_____.
二、圆的对称性
1.圆的对称性.
圆是_______图形,对称轴是_____________所在的直线.
相等
相等
轴对称
任何一条直径
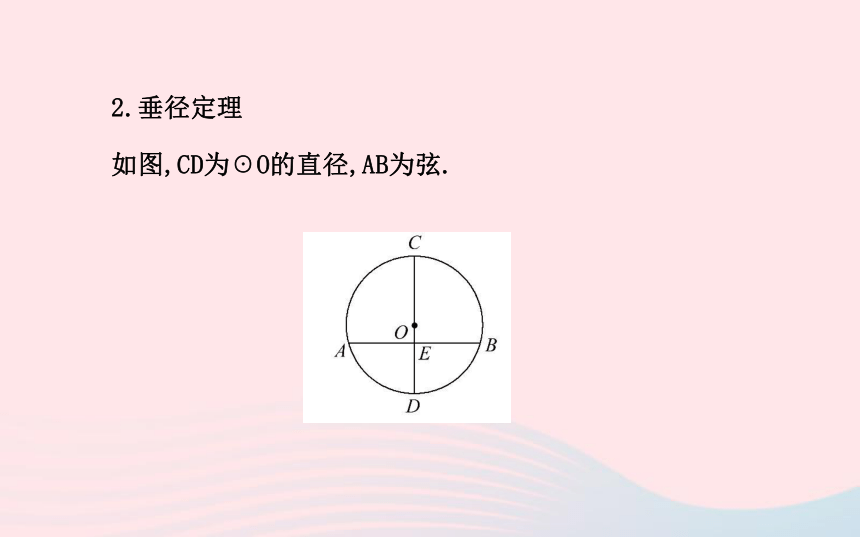
2.垂径定理
如图,CD为☉O的直径,AB为弦.
【思考】(1)当CD⊥AB,垂足为E时,将圆沿直线CD对折,点A与点
B重合吗?你会发现哪些相等的线段和相等的弧?
提示:重合.
(2)你能证明AE=BE吗?
提示:连结OA,OB,则OA=OB.
∵CD⊥AB,∴△OAE和△OBE都是直角三角形.
又∵OE为公共边,
∴两个直角三角形全等,则AE=BE.
(3)当AE=BE时,将圆沿直线CD对折, 与 与 相等
吗?
提示:连结OA,OB,
则OE为等腰△AOB底边上的中线,
∴CD⊥AB,∴点A与点B重合,
(4)上述证明是在△AOB存在即AB为非直径的弦的条件下得到
的结论,那么当AB为直径时是否成立呢?你能画出图形吗?
提示:成立.如图所示:
【总结】垂径定理:垂直于弦的直径_______,并且_____弦所对
的两条弧.
平分弦
平分
3.垂径定理的推论:平分弦(不是直径)的直径_____于这条弦,
并且_____弦所对的弧;平分弧的直径_________这条弧所对的
弦.
垂直
平分
垂直平分
(打“√”或“×”)
(1)圆心角相等,则它所对的弦及所对的弧都相等.( )
(2)在两个圆中,若有两条弦相等,则这两条弦所对的弧一定相
等.( )
(3)直径是所在圆的对称轴.( )
(4)弦的垂直平分线一定过圆心.( )
(5)平分弧的直线一定平分这条弧所对的弦.( )
×
×
×
√
×
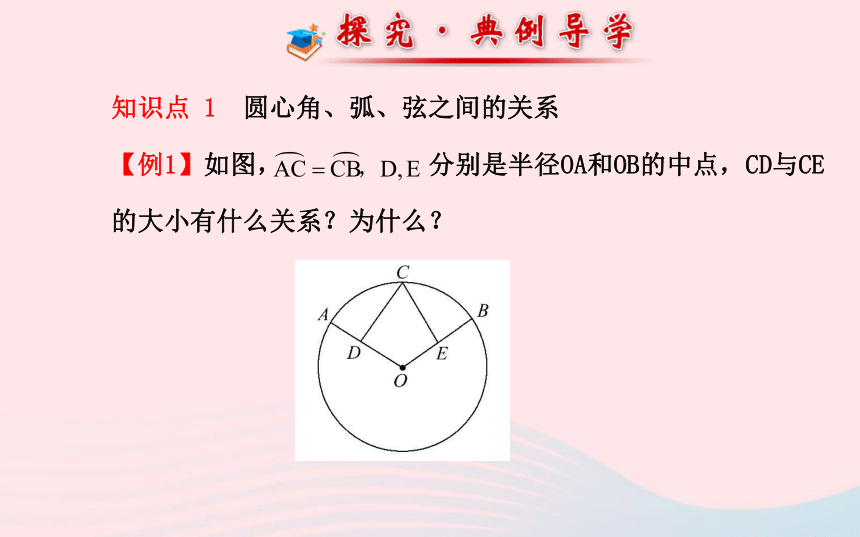
知识点 1 圆心角、弧、弦之间的关系
【例1】如图, 分别是半径OA和OB的中点,CD与CE
的大小有什么关系?为什么?
【解题探究】(1)由 如何添加辅助线构造相等的角?
提示:连结OC,根据弧相等,所对的圆心角也相等,可得
∠COD=∠COE.
(2)由D,E分别是半径OA和OB的中点,可得哪些线段相等?
提示:AO=BO,AD=OD=OE=EB.
3.通过以上探究,可证明哪两个三角形全等?
提示: 所以△ODC≌△OEC.
4.综上所述CD__CE(理由:_____________________)
全等三角形对应边相等
=
【总结提升】运用圆心角定理时应注意的两个问题
1.圆心角、弧、弦之间的关系的结论必须在同圆或等圆中才能成立.
2.一条弦所对的弧有两条,应用时应注意区分.
知识点 2 垂径定理及其应用
【例2】如图,⊙O的半径为17 cm,弦AB∥CD,AB=30 cm,
CD=16 cm,圆心O位于AB,CD的上方,求AB和CD间的距离.
【思路点拨】过圆心作两条弦的垂线,再通过连结圆心与弦的端点构造直角三角形,利用勾股定理求出AB和CD的距离.
【自主解答】分别过点O作弦AB,CD的垂线,设垂足分别为E,
F,
∵AB=30 cm,CD=16 cm,
在Rt△AOE中,
(cm).
在Rt△OCF中,
∴EF=OF-OE=15-8=7(cm).
【总结提升】在运用垂径定理时辅助线的作法及两点注意
1.辅助线作法:有关圆内弦的长度计算,一般情况下,经常过圆心作垂直于弦的半径,构建直角三角形.
2.两点注意:
(1)这里的垂径可以是直径、半径,也可以是过圆心的直线或线段.
(2)条件中的“弦”可以是直径,结论中的“平分弧”既意味着平分弦所对的劣弧,又意味着平分弦所对的优弧.
题组一:圆心角、弧、弦之间的关系
1.已知AB与A′B′分别是☉O与☉O′的两条弦,AB=A′B′,那
么∠AOB与∠A′O′B′的大小关系是( )
A.∠AOB=∠A′O′B′ B.∠AOB>∠A′O′B′
C.∠AOB<∠A′O′B′ D.不能确定
【解析】选D.由弦相等推弦所对的圆心角相等,必须保证在同
圆或等圆中.而☉O与☉O′不一定是等圆,所以∠AOB与
∠A′O′B′的大小关系不能确定.
2.如图,已知:AB是⊙O的直径,C,D是 上的三等分点,
∠AOE=60°,则∠COE是( )
A.40° B.60°
C.80° D.120°
【解析】选C.∵∠AOE=60°,
∴∠BOE=180°-∠AOE=120°,
∴ 的度数是120°.
∵C,D是 上的三等分点,
∴ 与 的度数都是40°,
∴∠COE=80°.
3.如图,在⊙O中, ∠C=70°,则∠B=______度,
∠A=______度.
【解析】
∴∠B=∠C=70°,∠A=180°-2∠C=40°.
答案:70 40
4.如图,AB是☉O的直径,BC,CD,DA是☉O的弦,且BC=CD=DA,则
∠BCD=________.
【解析】连结OC,OD,
∵BC=CD=DA,
∴∠AOD=∠DOC=∠COB.
∵∠AOD+∠DOC+∠COB=180°,
∴∠AOD=∠DOC=∠COB=60°,
∴△AOD,△DOC,△COB都为等边三角形,
∴∠BCO=∠DCO=60°,
∴∠BCD=60°+60°=120°.
答案:120°
5.已知:如图,在⊙O中,AB=CD.
求证:∠AOC=∠BOD.
【证明】
即
∴∠AOC=∠BOD.
题组二:垂径定理及其应用
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成
立的是( )
A.CM=DM
B.
C.∠ACD=∠ADC
D.OM=MD
【解析】选D.∵AB是⊙O的直径,弦CD⊥AB,垂足为M,∴M为
CD的中点,即CM=DM,选项A成立;B为 的中点,即
选项B成立;在△ACM和△ADM中,∵AM=AM,∠AMC=∠AMD=
90°,CM=DM,∴△ACM≌△ADM,∴∠ACD=∠ADC,选项C成
立;而OM与MD不一定相等,选项D不成立.
2.(
3.(
4.(
【解析】如图所示,过点O作OD⊥AB交AB于点C,交圆于点D,连结
OB.
在☉O中,∵OD⊥AB,∴AC=BC=0.4m.
∵OB=0.5m,BC=0.4m,
∴OC=0.3m,
∴CD=0.5-0.3=0.2(m).
答案:0.2
5.如图,在同一平面内,有一组平行线l1,l2,l3,相邻两条平行线
之间的距离为4,点O在直线l1上,☉O与直线l3的交点为A,B,AB
=12,求☉O的半径.
【解析】过点O作OC⊥AB于C,连结OA.
在Rt△AOC中,∠ACO=90°,
OC=4×2=8,
∴⊙O的半径为10.
6.(
【解析】由垂径定理得 设圆O半径为
x m,则OF=(x-1)m.在Rt△OBF中,根据勾股定理得x2=1.52+(x-
1)2,解得x=1.625,即圆O的半径是1.625m.
【想一想错在哪?】在半径为1的圆中,有两条弦AB,AC,其中
求∠BAC的度数.
提示:圆心O与两条弦AB,AC所组成的∠BAC的位置关系有两种情况:一种是圆心O在∠BAC的内部,另一种是圆心O在∠BAC的外部,这样得到的∠BAC的度数就有两个.解题时忽略圆心O在∠BAC的外部的情况,导致答案不完整,出现错误.
2.圆的对称性
1.理解圆的对称性.
2.掌握圆心角、弧、弦三者之间的关系,能运用它们之间的关系解决问题.(重点)
3.掌握垂径定理及其推论,能运用垂径定理及其推论解决问题.(重点、难点)
一、圆心角、弧、弦之间的关系
在同一个圆中,如果两个圆心角、两条弧、两条弦中有一组量
_____,那么它们所对应的其余各组量都分别_____.
二、圆的对称性
1.圆的对称性.
圆是_______图形,对称轴是_____________所在的直线.
相等
相等
轴对称
任何一条直径
2.垂径定理
如图,CD为☉O的直径,AB为弦.
【思考】(1)当CD⊥AB,垂足为E时,将圆沿直线CD对折,点A与点
B重合吗?你会发现哪些相等的线段和相等的弧?
提示:重合.
(2)你能证明AE=BE吗?
提示:连结OA,OB,则OA=OB.
∵CD⊥AB,∴△OAE和△OBE都是直角三角形.
又∵OE为公共边,
∴两个直角三角形全等,则AE=BE.
(3)当AE=BE时,将圆沿直线CD对折, 与 与 相等
吗?
提示:连结OA,OB,
则OE为等腰△AOB底边上的中线,
∴CD⊥AB,∴点A与点B重合,
(4)上述证明是在△AOB存在即AB为非直径的弦的条件下得到
的结论,那么当AB为直径时是否成立呢?你能画出图形吗?
提示:成立.如图所示:
【总结】垂径定理:垂直于弦的直径_______,并且_____弦所对
的两条弧.
平分弦
平分
3.垂径定理的推论:平分弦(不是直径)的直径_____于这条弦,
并且_____弦所对的弧;平分弧的直径_________这条弧所对的
弦.
垂直
平分
垂直平分
(打“√”或“×”)
(1)圆心角相等,则它所对的弦及所对的弧都相等.( )
(2)在两个圆中,若有两条弦相等,则这两条弦所对的弧一定相
等.( )
(3)直径是所在圆的对称轴.( )
(4)弦的垂直平分线一定过圆心.( )
(5)平分弧的直线一定平分这条弧所对的弦.( )
×
×
×
√
×
知识点 1 圆心角、弧、弦之间的关系
【例1】如图, 分别是半径OA和OB的中点,CD与CE
的大小有什么关系?为什么?
【解题探究】(1)由 如何添加辅助线构造相等的角?
提示:连结OC,根据弧相等,所对的圆心角也相等,可得
∠COD=∠COE.
(2)由D,E分别是半径OA和OB的中点,可得哪些线段相等?
提示:AO=BO,AD=OD=OE=EB.
3.通过以上探究,可证明哪两个三角形全等?
提示: 所以△ODC≌△OEC.
4.综上所述CD__CE(理由:_____________________)
全等三角形对应边相等
=
【总结提升】运用圆心角定理时应注意的两个问题
1.圆心角、弧、弦之间的关系的结论必须在同圆或等圆中才能成立.
2.一条弦所对的弧有两条,应用时应注意区分.
知识点 2 垂径定理及其应用
【例2】如图,⊙O的半径为17 cm,弦AB∥CD,AB=30 cm,
CD=16 cm,圆心O位于AB,CD的上方,求AB和CD间的距离.
【思路点拨】过圆心作两条弦的垂线,再通过连结圆心与弦的端点构造直角三角形,利用勾股定理求出AB和CD的距离.
【自主解答】分别过点O作弦AB,CD的垂线,设垂足分别为E,
F,
∵AB=30 cm,CD=16 cm,
在Rt△AOE中,
(cm).
在Rt△OCF中,
∴EF=OF-OE=15-8=7(cm).
【总结提升】在运用垂径定理时辅助线的作法及两点注意
1.辅助线作法:有关圆内弦的长度计算,一般情况下,经常过圆心作垂直于弦的半径,构建直角三角形.
2.两点注意:
(1)这里的垂径可以是直径、半径,也可以是过圆心的直线或线段.
(2)条件中的“弦”可以是直径,结论中的“平分弧”既意味着平分弦所对的劣弧,又意味着平分弦所对的优弧.
题组一:圆心角、弧、弦之间的关系
1.已知AB与A′B′分别是☉O与☉O′的两条弦,AB=A′B′,那
么∠AOB与∠A′O′B′的大小关系是( )
A.∠AOB=∠A′O′B′ B.∠AOB>∠A′O′B′
C.∠AOB<∠A′O′B′ D.不能确定
【解析】选D.由弦相等推弦所对的圆心角相等,必须保证在同
圆或等圆中.而☉O与☉O′不一定是等圆,所以∠AOB与
∠A′O′B′的大小关系不能确定.
2.如图,已知:AB是⊙O的直径,C,D是 上的三等分点,
∠AOE=60°,则∠COE是( )
A.40° B.60°
C.80° D.120°
【解析】选C.∵∠AOE=60°,
∴∠BOE=180°-∠AOE=120°,
∴ 的度数是120°.
∵C,D是 上的三等分点,
∴ 与 的度数都是40°,
∴∠COE=80°.
3.如图,在⊙O中, ∠C=70°,则∠B=______度,
∠A=______度.
【解析】
∴∠B=∠C=70°,∠A=180°-2∠C=40°.
答案:70 40
4.如图,AB是☉O的直径,BC,CD,DA是☉O的弦,且BC=CD=DA,则
∠BCD=________.
【解析】连结OC,OD,
∵BC=CD=DA,
∴∠AOD=∠DOC=∠COB.
∵∠AOD+∠DOC+∠COB=180°,
∴∠AOD=∠DOC=∠COB=60°,
∴△AOD,△DOC,△COB都为等边三角形,
∴∠BCO=∠DCO=60°,
∴∠BCD=60°+60°=120°.
答案:120°
5.已知:如图,在⊙O中,AB=CD.
求证:∠AOC=∠BOD.
【证明】
即
∴∠AOC=∠BOD.
题组二:垂径定理及其应用
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成
立的是( )
A.CM=DM
B.
C.∠ACD=∠ADC
D.OM=MD
【解析】选D.∵AB是⊙O的直径,弦CD⊥AB,垂足为M,∴M为
CD的中点,即CM=DM,选项A成立;B为 的中点,即
选项B成立;在△ACM和△ADM中,∵AM=AM,∠AMC=∠AMD=
90°,CM=DM,∴△ACM≌△ADM,∴∠ACD=∠ADC,选项C成
立;而OM与MD不一定相等,选项D不成立.
2.(
3.(
4.(
【解析】如图所示,过点O作OD⊥AB交AB于点C,交圆于点D,连结
OB.
在☉O中,∵OD⊥AB,∴AC=BC=0.4m.
∵OB=0.5m,BC=0.4m,
∴OC=0.3m,
∴CD=0.5-0.3=0.2(m).
答案:0.2
5.如图,在同一平面内,有一组平行线l1,l2,l3,相邻两条平行线
之间的距离为4,点O在直线l1上,☉O与直线l3的交点为A,B,AB
=12,求☉O的半径.
【解析】过点O作OC⊥AB于C,连结OA.
在Rt△AOC中,∠ACO=90°,
OC=4×2=8,
∴⊙O的半径为10.
6.(
【解析】由垂径定理得 设圆O半径为
x m,则OF=(x-1)m.在Rt△OBF中,根据勾股定理得x2=1.52+(x-
1)2,解得x=1.625,即圆O的半径是1.625m.
【想一想错在哪?】在半径为1的圆中,有两条弦AB,AC,其中
求∠BAC的度数.
提示:圆心O与两条弦AB,AC所组成的∠BAC的位置关系有两种情况:一种是圆心O在∠BAC的内部,另一种是圆心O在∠BAC的外部,这样得到的∠BAC的度数就有两个.解题时忽略圆心O在∠BAC的外部的情况,导致答案不完整,出现错误.
