华东师大版九年级数学下册第27章圆27.1.3圆周角 习题课件(42张PPT)
文档属性
| 名称 | 华东师大版九年级数学下册第27章圆27.1.3圆周角 习题课件(42张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 20:29:06 | ||
图片预览









文档简介
(共42张PPT)
3.圆周角
1.理解圆周角的概念,会判断一个角是否为圆周角.(重点)
2.掌握直径所对圆周角的特征和圆周角的性质,会推导圆周角定理,能运用圆周角定理解决问题.(重点、难点)
3.通过结合圆周角定理的推导过程,渗透特殊到一般、转化与化归等数学思想.(难点)
圆周角的概念、性质及圆周角定理
1.圆周角:顶点在_____,并且两边都与圆_____的角叫做圆周
角.
2.半圆或直径所对的圆周角:
(1)性质:半圆或直径所对的圆周角都_____,都等于____.
(2)应用:_____的圆周角所对的弦是圆的直径.
圆上
相交
相等
90°
90°
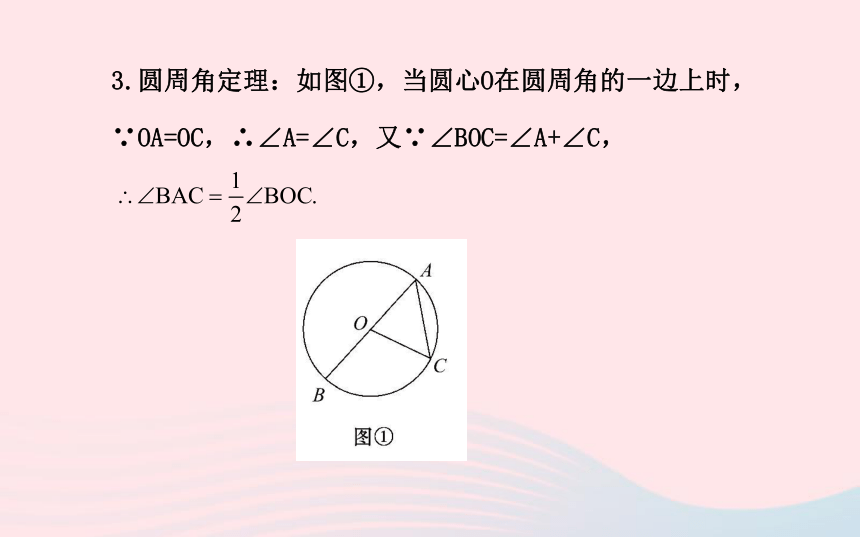
3.圆周角定理:如图①,当圆心O在圆周角的一边上时,
∵OA=OC,∴∠A=∠C,又∵∠BOC=∠A+∠C,
【思考】 (1)如图②,当圆心O在圆周角的内部时,∠BAC与
∠BOC的上述关系是否还成立?为什么?
提示:_____.理由如下:
作直径AD.
由图①推理得:∠BAD=_______.
同理:∠CAD=________.
∴∠BAD+∠CAD=_________________,
即∠BAC=________.
成立
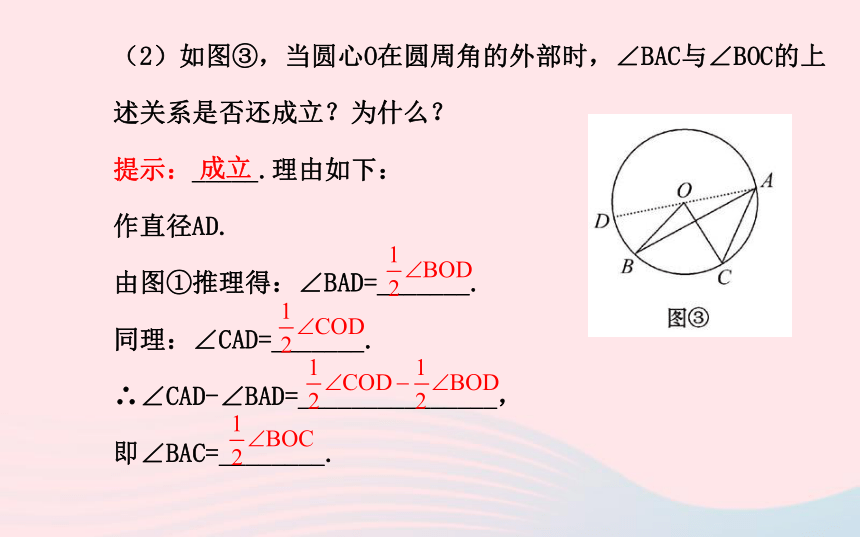
(2)如图③,当圆心O在圆周角的外部时,∠BAC与∠BOC的上
述关系是否还成立?为什么?
提示:_____.理由如下:
作直径AD.
由图①推理得:∠BAD=_______.
同理:∠CAD=_______.
∴∠CAD-∠BAD=_______________,
即∠BAC=________.
成立
【总结】圆周角定理:①在一个圆中,一条弧所对的圆周角等
于其所对的圆心角的_____.
②在同圆或等圆中,同弧或等弧所对的圆周角_____.
③在同圆或等圆中相等的圆周角所对的弧也_____.
一半
相等
相等
(打“√”或“×”)
(1)顶点在圆上的角叫做圆周角.( )
(2)同弧所对的圆周角相等.( )
(3)90°的圆周角所对的弧为半圆.( )
(4)在同圆中,圆周角相等,所对的弦也相等.( )
(5)在等圆中,弧相等,则它所对的圆周角、圆心角及所对
的弦都相等.( )
×
√
√
√
√
知识点 1 圆周角定理
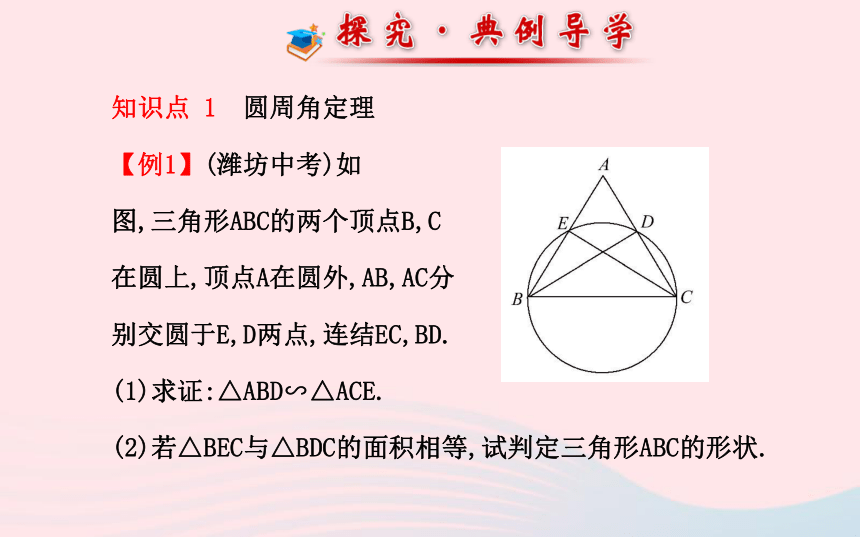
【例1】(潍坊中考)如
图,三角形ABC的两个顶点B,C
在圆上,顶点A在圆外,AB,AC分
别交圆于E,D两点,连结EC,BD.
(1)求证:△ABD∽△ACE.
(2)若△BEC与△BDC的面积相等,试判定三角形ABC的形状.
【解题探究】(1)①△ABD与△ACE中,有相等的角吗?
提示:有一公共角,∠BAD=∠CAE.
②如何找出△ABD与△ACE中另外相等的一组角?
提示:∵ 所对的圆周角相等,
∴∠EBD=∠ECD.
③由①②可知△ABD与△ACE有_______________,所以可以得出
△ABD∽△ACE.
两对对应角相等
(2)①如何说明S△ACE=S△ABD?
提示:∵S△BEC=S△BCD,S△ACE=S△ABC-S△BEC,S△ABD=S△ABC-S△BCD,
∴S△ACE=S△ABD.
②由①的S△ACE=S△ABD,结合(1)的△ABD∽△ACE,可以得出△ABD
与△ACE对应边之比等于__,即AB=___,所以△ABC为_____三角
形.
1
AC
等腰
【总结提升】利用圆周角定理进行证明时的两点注意
1.圆周角定理适用的范围是在同圆或等圆中.
2.在证明时,此定理可以直接作为已知条件使用.
知识点 2 圆周角定理的综合应用
【例2】(沈阳中考)如图,☉O是△ABC的外接圆,AB是☉O
的直径,D为☉O上一点,OD⊥AC,垂足为E,连结BD.
(1)求证:BD平分∠ABC.
(2)当∠ODB=30°时,求证:BC=OD.
【思路点拨】(1)由OD⊥AC,OD为半径,根据垂径定理,即可得
又由在同圆或等圆中,同弧或等弧所对的圆周角相等,
即可证得BD平分∠ABC.
(2)首先由OB=OD,易求得∠AOD的度数,又由OD⊥AC于E,可求得
∠A的度数,然后由AB是☉O的直径,根据圆周角定理,可得
∠ACB=90°,继而可证得BC=OD.
【自主解答】(1)∵OD⊥AC,OD为半径,
∴∠CBD=∠ABD,
∴BD平分∠ABC.
(2)∵OB=OD,
∴∠OBD=∠ODB=30°,
∴∠AOD=∠OBD+∠ODB=30°+30°=60°.
又∵OD⊥AC于E,
∴∠OEA=90°,
∴∠A=180°-∠OEA-∠AOD=180°-90°-60°=30°.
又∵AB为☉O的直径,
∴∠ACB=90°,
在Rt△ACB中,
∴BC=OD.
【总结提升】利用圆周角定理推论的两种思路
1.见直径,通常构建90°的圆周角,利用直角三角形知识解决.
2.见90°的圆周角,通常作直径,构建直角三角形.
题组一:圆周角定理
1.(滨州中考)如图,在☉O中,圆心角∠BOC=78°,则圆周
角∠BAC的大小为( )
A.156° B.78° C.39° D.12°
【解析】选C.根据在同圆或等圆中,同弧或等弧所对的圆周角
是它所对的圆心角的一半,所以
2.已知AB,CD是☉O的两条直径,∠ABC=30°,那么∠BAD=( )
A.45° B.60°
C.90° D.30°
【解析】选D.因为∠ABC与∠ADC是
同一条弧所对的圆周角,所以∠ABC
=∠ADC=30°.又因为OD=OA,所以
∠BAD=∠ADC=30°.
3.(邵阳中考)如图,弦AB,CD相交于点O,连结AD,BC,在
不添加辅助线的情况下,请在图中找出一对相等的角,它们
是________.
【解析】由对顶角相等,可得到∠AOC=∠BOD,∠AOD=∠BOC;
由同弧所对的圆周角相等,可得到∠A=∠C,∠B=∠D.
答案:本题答案不唯一,如∠A=∠C等
4.(黔西南州中考)如图所示,已知∠BAC=∠CDA=20°,
则∠ABO的度数为________.
【解析】连结OA,OC,
则∠COB=2∠BAC=40°,∠AOC=2∠CDA=40°,
所以∠AOB=80°,
所以∠ABO=(180°-80°)÷2=50°.
答案:50°
5.如图,△ABC内接于☉O,AB=8,AC=4,D是AB边上一点,P是优弧
BAC的中点,连结PA,PB,PC,PD,当BD的长度为多少时,△PAD是以
AD为底边的等腰三角形?并加以证明.
【解析】当BD=4时,△PAD是以AD为底边的等腰三角形.理由
如下:
∵P是优弧BAC的中点,
∴
∴PB=PC.
在△PBD与△PCA中,
∴△PBD≌△PCA(S.A.S.).
∴PD=PA,
即BD=4时,△PAD是以AD为底边的等腰三角形.
题组二:圆周角定理的综合应用
1.(舟山中考)如图,⊙O的半径OD⊥弦AB于点C,连
结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的
长为( )
【解析】选D.连结BE,根据直径所对的圆周角为直角,知BE⊥AB,
BE∥OC且BE=2OC,根据垂径定理得,AC=4,OC=OD-CD=OA-2,在
△ACO中,根据勾股定理得,AC2+OC2=AO2,即42+(OA-2)2=AO2,得
OA=5,OC=3,BE=6,在△BCE中,根据勾股定理得,EC2=BC2+BE2=
2.如图,已知☉O的两条弦AB,CD相交于AB的中点E,且AB=4,
DE=CE+3,则CD的长为( )
A.4 B.5 C.8 D.10
【解析】选B.连结AC,BD,如图,
∵∠A=∠D ,∠C=∠B,
∴△AEC∽△DEB,
∴AE·BE=CE·DE.
设CE=x,则DE=3+x.
∴x(x+3)=2×2,
解得,x=1或x=-4(不合题意,应舍去).
∴CE=1,∴CD=3+1+1=5.
【变式备选】如图,已知AB为☉O的直径,C为☉O上一点,CD⊥AB
于D,AD=9,BD=4,以C为圆心,CD为半径的圆与☉O相交于P,Q两点,
弦PQ交CD于E,则PE·EQ的值是( )
A.24 B.9
C.6 D.27
【解析】选D.延长DC交☉C于M,延长CD交☉O于N,连结PC,NQ.
连结AC,BC,
∵AB为☉O的直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°.
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠CAD+∠ACD=90°,
∴∠ACD=∠ABC,
∴△ACD∽△CBD,
∵AD=9,BD=4,∴CD=6.
在☉O中,∠PCN=∠NQP,∠CPQ=∠QNC,
∴△PEC∽△NEQ,
∴PE·QE=CE·NE,
同理,在☉C中,可得,PE·QE=DE·ME,
设CE=x,则DE=6-x,
则(6-x)(x+6)=x(6-x+6),
解得x=3.
所以,CE=3,DE=6-3=3,EM=6+3=9.
所以PE·EQ=3×9=27.
3.(常州中考)如图,△ABC内接于☉O,∠BAC=120°,
AB=AC,BD为☉O的直径,AD=6,则DC=____________.
【解析】因为∠BAC=120°,AB=AC,所以∠ABC=∠ACB=30°,
所以∠BDA=30°,因为BD为直径,所以∠BAD=90°,
所以∠ABD=60°,所以∠DBC=30°.
在Rt△ABD中,
在Rt△BCD中,
答案:
4.如图,AB,CD是☉O的弦,AB⊥CD,BE是☉O的直径.若AC=3,
则DE=________.
【解析】连结AE,∵BE是⊙O的直径,
∴∠BAE=90°,即AB⊥AE.
∵AB⊥CD,∴AE∥CD,
∴∠ACD+∠CAE=180°.
∵四边形ACDE是⊙O的内接四边形,
∴∠CAE+∠CDE=180°,
∴∠ACD=∠CDE,
答案:3
5.如图,在☉O中,直径AB与弦CD相交于点P,
∠CAB=40°,∠APD=65°.
(1)求∠B的大小.
(2)已知AD=6,求圆心O到BD的距离.
【解析】(1)∵∠APD=∠C+∠CAB,
∴∠C=65°-40°=25°,
∴∠B=∠C=25°.
(2)作OE⊥BD于E,则DE=BE,
又∵AO=BO,
圆心O到BD的距离为3.
【想一想错在哪?】AB是⊙O的直径,AC是⊙O的弦,AB=2,
∠BAC=30°.在图中画出弦AD,使AD=1,则∠CAD的度数为
______.
提示:弦AD与AC的位置关系有两种情况:一种是弦AD与AC在直径AB的同侧,另一种是弦AD与AC在直径AB的异侧,因而∠CAD的度数有两个.解题过程中遗漏弦AD与AC在直径AB的异侧这种情况,使解题结果不完整,产生错误.
3.圆周角
1.理解圆周角的概念,会判断一个角是否为圆周角.(重点)
2.掌握直径所对圆周角的特征和圆周角的性质,会推导圆周角定理,能运用圆周角定理解决问题.(重点、难点)
3.通过结合圆周角定理的推导过程,渗透特殊到一般、转化与化归等数学思想.(难点)
圆周角的概念、性质及圆周角定理
1.圆周角:顶点在_____,并且两边都与圆_____的角叫做圆周
角.
2.半圆或直径所对的圆周角:
(1)性质:半圆或直径所对的圆周角都_____,都等于____.
(2)应用:_____的圆周角所对的弦是圆的直径.
圆上
相交
相等
90°
90°
3.圆周角定理:如图①,当圆心O在圆周角的一边上时,
∵OA=OC,∴∠A=∠C,又∵∠BOC=∠A+∠C,
【思考】 (1)如图②,当圆心O在圆周角的内部时,∠BAC与
∠BOC的上述关系是否还成立?为什么?
提示:_____.理由如下:
作直径AD.
由图①推理得:∠BAD=_______.
同理:∠CAD=________.
∴∠BAD+∠CAD=_________________,
即∠BAC=________.
成立
(2)如图③,当圆心O在圆周角的外部时,∠BAC与∠BOC的上
述关系是否还成立?为什么?
提示:_____.理由如下:
作直径AD.
由图①推理得:∠BAD=_______.
同理:∠CAD=_______.
∴∠CAD-∠BAD=_______________,
即∠BAC=________.
成立
【总结】圆周角定理:①在一个圆中,一条弧所对的圆周角等
于其所对的圆心角的_____.
②在同圆或等圆中,同弧或等弧所对的圆周角_____.
③在同圆或等圆中相等的圆周角所对的弧也_____.
一半
相等
相等
(打“√”或“×”)
(1)顶点在圆上的角叫做圆周角.( )
(2)同弧所对的圆周角相等.( )
(3)90°的圆周角所对的弧为半圆.( )
(4)在同圆中,圆周角相等,所对的弦也相等.( )
(5)在等圆中,弧相等,则它所对的圆周角、圆心角及所对
的弦都相等.( )
×
√
√
√
√
知识点 1 圆周角定理
【例1】(潍坊中考)如
图,三角形ABC的两个顶点B,C
在圆上,顶点A在圆外,AB,AC分
别交圆于E,D两点,连结EC,BD.
(1)求证:△ABD∽△ACE.
(2)若△BEC与△BDC的面积相等,试判定三角形ABC的形状.
【解题探究】(1)①△ABD与△ACE中,有相等的角吗?
提示:有一公共角,∠BAD=∠CAE.
②如何找出△ABD与△ACE中另外相等的一组角?
提示:∵ 所对的圆周角相等,
∴∠EBD=∠ECD.
③由①②可知△ABD与△ACE有_______________,所以可以得出
△ABD∽△ACE.
两对对应角相等
(2)①如何说明S△ACE=S△ABD?
提示:∵S△BEC=S△BCD,S△ACE=S△ABC-S△BEC,S△ABD=S△ABC-S△BCD,
∴S△ACE=S△ABD.
②由①的S△ACE=S△ABD,结合(1)的△ABD∽△ACE,可以得出△ABD
与△ACE对应边之比等于__,即AB=___,所以△ABC为_____三角
形.
1
AC
等腰
【总结提升】利用圆周角定理进行证明时的两点注意
1.圆周角定理适用的范围是在同圆或等圆中.
2.在证明时,此定理可以直接作为已知条件使用.
知识点 2 圆周角定理的综合应用
【例2】(沈阳中考)如图,☉O是△ABC的外接圆,AB是☉O
的直径,D为☉O上一点,OD⊥AC,垂足为E,连结BD.
(1)求证:BD平分∠ABC.
(2)当∠ODB=30°时,求证:BC=OD.
【思路点拨】(1)由OD⊥AC,OD为半径,根据垂径定理,即可得
又由在同圆或等圆中,同弧或等弧所对的圆周角相等,
即可证得BD平分∠ABC.
(2)首先由OB=OD,易求得∠AOD的度数,又由OD⊥AC于E,可求得
∠A的度数,然后由AB是☉O的直径,根据圆周角定理,可得
∠ACB=90°,继而可证得BC=OD.
【自主解答】(1)∵OD⊥AC,OD为半径,
∴∠CBD=∠ABD,
∴BD平分∠ABC.
(2)∵OB=OD,
∴∠OBD=∠ODB=30°,
∴∠AOD=∠OBD+∠ODB=30°+30°=60°.
又∵OD⊥AC于E,
∴∠OEA=90°,
∴∠A=180°-∠OEA-∠AOD=180°-90°-60°=30°.
又∵AB为☉O的直径,
∴∠ACB=90°,
在Rt△ACB中,
∴BC=OD.
【总结提升】利用圆周角定理推论的两种思路
1.见直径,通常构建90°的圆周角,利用直角三角形知识解决.
2.见90°的圆周角,通常作直径,构建直角三角形.
题组一:圆周角定理
1.(滨州中考)如图,在☉O中,圆心角∠BOC=78°,则圆周
角∠BAC的大小为( )
A.156° B.78° C.39° D.12°
【解析】选C.根据在同圆或等圆中,同弧或等弧所对的圆周角
是它所对的圆心角的一半,所以
2.已知AB,CD是☉O的两条直径,∠ABC=30°,那么∠BAD=( )
A.45° B.60°
C.90° D.30°
【解析】选D.因为∠ABC与∠ADC是
同一条弧所对的圆周角,所以∠ABC
=∠ADC=30°.又因为OD=OA,所以
∠BAD=∠ADC=30°.
3.(邵阳中考)如图,弦AB,CD相交于点O,连结AD,BC,在
不添加辅助线的情况下,请在图中找出一对相等的角,它们
是________.
【解析】由对顶角相等,可得到∠AOC=∠BOD,∠AOD=∠BOC;
由同弧所对的圆周角相等,可得到∠A=∠C,∠B=∠D.
答案:本题答案不唯一,如∠A=∠C等
4.(黔西南州中考)如图所示,已知∠BAC=∠CDA=20°,
则∠ABO的度数为________.
【解析】连结OA,OC,
则∠COB=2∠BAC=40°,∠AOC=2∠CDA=40°,
所以∠AOB=80°,
所以∠ABO=(180°-80°)÷2=50°.
答案:50°
5.如图,△ABC内接于☉O,AB=8,AC=4,D是AB边上一点,P是优弧
BAC的中点,连结PA,PB,PC,PD,当BD的长度为多少时,△PAD是以
AD为底边的等腰三角形?并加以证明.
【解析】当BD=4时,△PAD是以AD为底边的等腰三角形.理由
如下:
∵P是优弧BAC的中点,
∴
∴PB=PC.
在△PBD与△PCA中,
∴△PBD≌△PCA(S.A.S.).
∴PD=PA,
即BD=4时,△PAD是以AD为底边的等腰三角形.
题组二:圆周角定理的综合应用
1.(舟山中考)如图,⊙O的半径OD⊥弦AB于点C,连
结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的
长为( )
【解析】选D.连结BE,根据直径所对的圆周角为直角,知BE⊥AB,
BE∥OC且BE=2OC,根据垂径定理得,AC=4,OC=OD-CD=OA-2,在
△ACO中,根据勾股定理得,AC2+OC2=AO2,即42+(OA-2)2=AO2,得
OA=5,OC=3,BE=6,在△BCE中,根据勾股定理得,EC2=BC2+BE2=
2.如图,已知☉O的两条弦AB,CD相交于AB的中点E,且AB=4,
DE=CE+3,则CD的长为( )
A.4 B.5 C.8 D.10
【解析】选B.连结AC,BD,如图,
∵∠A=∠D ,∠C=∠B,
∴△AEC∽△DEB,
∴AE·BE=CE·DE.
设CE=x,则DE=3+x.
∴x(x+3)=2×2,
解得,x=1或x=-4(不合题意,应舍去).
∴CE=1,∴CD=3+1+1=5.
【变式备选】如图,已知AB为☉O的直径,C为☉O上一点,CD⊥AB
于D,AD=9,BD=4,以C为圆心,CD为半径的圆与☉O相交于P,Q两点,
弦PQ交CD于E,则PE·EQ的值是( )
A.24 B.9
C.6 D.27
【解析】选D.延长DC交☉C于M,延长CD交☉O于N,连结PC,NQ.
连结AC,BC,
∵AB为☉O的直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°.
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠CAD+∠ACD=90°,
∴∠ACD=∠ABC,
∴△ACD∽△CBD,
∵AD=9,BD=4,∴CD=6.
在☉O中,∠PCN=∠NQP,∠CPQ=∠QNC,
∴△PEC∽△NEQ,
∴PE·QE=CE·NE,
同理,在☉C中,可得,PE·QE=DE·ME,
设CE=x,则DE=6-x,
则(6-x)(x+6)=x(6-x+6),
解得x=3.
所以,CE=3,DE=6-3=3,EM=6+3=9.
所以PE·EQ=3×9=27.
3.(常州中考)如图,△ABC内接于☉O,∠BAC=120°,
AB=AC,BD为☉O的直径,AD=6,则DC=____________.
【解析】因为∠BAC=120°,AB=AC,所以∠ABC=∠ACB=30°,
所以∠BDA=30°,因为BD为直径,所以∠BAD=90°,
所以∠ABD=60°,所以∠DBC=30°.
在Rt△ABD中,
在Rt△BCD中,
答案:
4.如图,AB,CD是☉O的弦,AB⊥CD,BE是☉O的直径.若AC=3,
则DE=________.
【解析】连结AE,∵BE是⊙O的直径,
∴∠BAE=90°,即AB⊥AE.
∵AB⊥CD,∴AE∥CD,
∴∠ACD+∠CAE=180°.
∵四边形ACDE是⊙O的内接四边形,
∴∠CAE+∠CDE=180°,
∴∠ACD=∠CDE,
答案:3
5.如图,在☉O中,直径AB与弦CD相交于点P,
∠CAB=40°,∠APD=65°.
(1)求∠B的大小.
(2)已知AD=6,求圆心O到BD的距离.
【解析】(1)∵∠APD=∠C+∠CAB,
∴∠C=65°-40°=25°,
∴∠B=∠C=25°.
(2)作OE⊥BD于E,则DE=BE,
又∵AO=BO,
圆心O到BD的距离为3.
【想一想错在哪?】AB是⊙O的直径,AC是⊙O的弦,AB=2,
∠BAC=30°.在图中画出弦AD,使AD=1,则∠CAD的度数为
______.
提示:弦AD与AC的位置关系有两种情况:一种是弦AD与AC在直径AB的同侧,另一种是弦AD与AC在直径AB的异侧,因而∠CAD的度数有两个.解题过程中遗漏弦AD与AC在直径AB的异侧这种情况,使解题结果不完整,产生错误.
