沪科版八下数学第18章 勾股定理达标测试卷(含答案)
文档属性
| 名称 | 沪科版八下数学第18章 勾股定理达标测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 180.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 18:44:19 | ||
图片预览



文档简介
第18章达标测试卷
一、选择题(每题3分,共30分)
1.在Rt△AOB中,∠AOB=90°,若AB=10,AO=6,则OB的长为( )
A.5 B.6 C.8 D.10
2.下列四组数中不能构成直角三角形三边长的一组是( )
A.1,2, B.3,5,4 C.5,12,13 D.4,13,15
3.直角三角形的一条直角边长是另一条直角边长的,斜边长为10,则它的面积为( )
A.10 B.15 C.20 D.30
4.如图,P是第一象限的平分线上一点,且OP=2,则P点的坐标为( )
A.(2,2)
B.(,)
C.(2,)
D.(,2)
5.若等腰直角三角形斜边上的高为1,则它的周长是( )
A.4 B.2+1 C.4 D.2+2
6.下列各组数是勾股数的是( )
A.6,7,8 B.1,,2 C.5,4,3 D.0.3,0.4,0.5
7.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三边长分别为5里,12里,13里,问这块沙田面积有多大?题中1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米
C.75平方千米 D.750平方千米
8.在△ABC中,AC=9,BC=12,AB=15,则AB边上的高是( )
A. B. C. D.
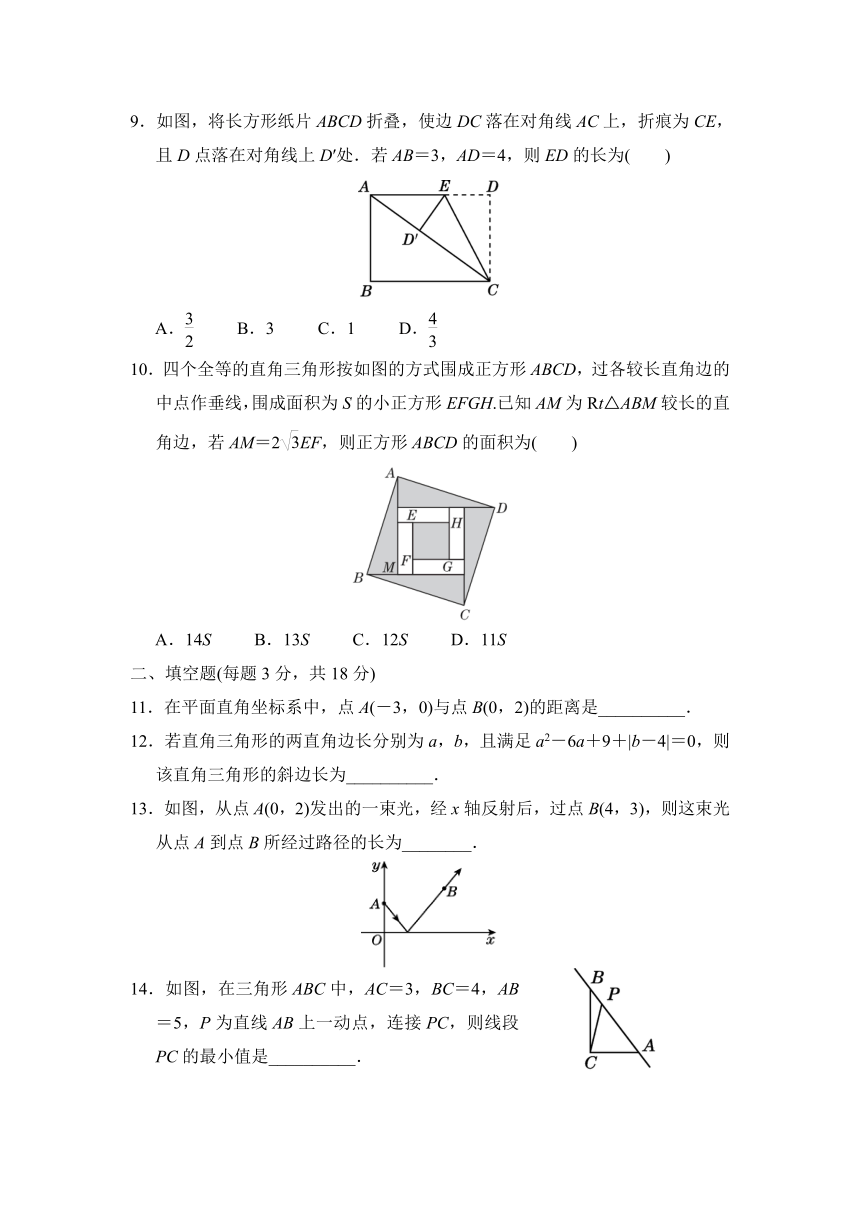
9.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线上D′处.若AB=3,AD=4,则ED的长为( )
A. B.3 C.1 D.
10.四个全等的直角三角形按如图的方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长的直角边,若AM=2EF,则正方形ABCD的面积为( )
A.14S B.13S C.12S D.11S
二、填空题(每题3分,共18分)
11.在平面直角坐标系中,点A(-3,0)与点B(0,2)的距离是__________.
12.若直角三角形的两直角边长分别为a,b,且满足a2-6a+9+|b-4|=0,则该直角三角形的斜边长为__________.
13.如图,从点A(0,2)发出的一束光,经x轴反射后,过点B(4,3),则这束光从点A到点B所经过路径的长为________.
14.如图,在三角形ABC中,AC=3,BC=4,AB=5,P为直线AB上一动点,连接PC,则线段PC的最小值是__________.
15.我国古代数学名著《九章算术》中有云:“今有木长二丈,围之三尺,葛生其下,缠木七周,上与木齐,问葛长几何?”大意:有一根木头长2丈,上、下底面的周长为3尺,葛藤生长在木下的A点,绕木7周,葛梢与木头上端B点刚好齐平(如图).则葛长是________尺.(注:1丈等于10尺,葛缠木以最短的路径向上长,误差忽略不计)
16.如图,在△ABC中,AB=AC=10 cm,BC=16 cm,现点P从点B出发,沿BC向C点运动,运动速度为cm/s,若点P的运动时间为t s,则当△ABP是直角三角形时,t的值是________.
三、解答题(17~20题每题8分,21~22题每题10分,共52分)
17.在△ABC中,∠C=90°,AB=20,若∠A=60°,求BC,AC的长.
18.如图,一艘船由A港沿北偏东60°方向航行10 km至B港,然后再沿北偏西30°方向航行10 km至C港.
(1)求A,C两港之间的距离(结果保留到0.1 km,参考数据:≈1.414,≈1.732);
(2)确定C港在A港的什么方向.
INCLUDEPICTURE"HKJJJ26.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\HKJJJ26.tif" \* MERGEFORMATINET
19.如图,在B港有甲、乙两艘渔船,若甲渔船沿北偏东60°方向以每小时8海里的速度前进,乙渔船沿南偏东30°方向以每小时15海里的速度前进,两小时后,甲船到达M岛,乙船到达P岛.求P岛与M岛之间的距离.
INCLUDEPICTURE"8SXHK59.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\8SXHK59.tif" \* MERGEFORMATINET
20.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
INCLUDEPICTURE"F10.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\F10.tif" \* MERGEFORMATINET
21.在△ABC中,BC=a,AC=b,AB=c,设c为最长边长,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边长分别为6,8,9时,△ABC为________三角形;当△ABC三边长分别为6,8,11时,△ABC为________三角形.
(2)猜想:当a2+b2________c2时,△ABC为锐角三角形;当a2+b2________c2时,△ABC为钝角三角形.
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
22.如图,将长方形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将长方形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当m=3时,点B的坐标为________,点E的坐标为________;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
INCLUDEPICTURE"i71.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\i71.tif" \* MERGEFORMATINET
答案
一、1.C 2.D
3.B 点拨:设较短直角边长为x(x>0),则有x2+(3x)2=102,解得x=,∴直角三角形的面积S=x·3x=15.
4.B 5.D 6.C
7.A 点拨:由题意可得三角形沙田的三边长为2.5千米,6千米,6.5千米.因为2.52+62=6.52,所以这个三角形为直角三角形,直角边长为2.5千米和6千米,所以S=×6×2.5=7.5(平方千米),故选A.
8.A
9.A 点拨:在Rt△ABC中,AC===5.设ED=x,则D′E=x,AE=4-x,在Rt△AD′E中,AD′=AC-CD′=2,根据勾股定理可得方程22+x2=(4-x)2,再解方程即可.
10.B 点拨:设AM=2a,BM=b,则正方形ABCD的面积=4a2+b2.
由题意知EF=(2a-b)-2(a-b)=2a-b-2a+2b=b.
∵AM=2EF,∴2a=2b,
∴a=b.
∵正方形EFGH的面积为S,
∴b2=S,
∴正方形ABCD的面积=4a2+b2=13b2=13S.故选B.
二、11.
12.5 点拨:∵a2-6a+9+|b-4|=0,∴(a-3)2+|b-4|=0,∴a-3=0,b-4=0,解得a=3,b=4,
∴该直角三角形的斜边长===5.
13. 14. 15.29
16.32或50 点拨:如图①,当∠APB=90°时,AP⊥BC,∵AB=AC,AP⊥BC,∴BP=CP=BC=8 cm,∴t=8,解得t=32;如图②,当∠PAB=90°时,过点A作AE⊥BC于点E.
∵AB=AC,AE⊥BC,∴BE=CE=BC=8 cm,∴PE=BP-BE=cm.在Rt△AEC中,AE2=AC2-CE2,即AE2=102-82,解得AE=6 cm,在Rt△PAB中,AP2=BP2-AB2,在Rt△AEP中,AP2=PE2+AE2,
∴-100=+36,解得t=50.综上所述,t的值为32或50.
INCLUDEPICTURE"8SXHK74.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\8SXHK74.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\8SXHK74.tif" \* MERGEFORMATINET
三、17.解:∵∠C=90°,∠A=60°,
∴∠B=180°-∠C-∠A=180°-90°-60°=30°.
∴AC=AB=×20=10.
在Rt△ABC中,由勾股定理得BC===10.
18.解:(1)由题意得∠PBC=30°,∠MAB=60°,
∴∠CBQ=60°,∠BAN=30°,
∴∠ABQ=30°,∴∠ABC=90°.
∵AB=BC=10,
∴AC==10≈14.1.
答:A、C两港之间的距离约为14.1 km.
(2)由(1)知,△ABC为等腰直角三角形,
∴∠BAC=45°,∴∠CAM=60°-45°=15°,
∴C港在A港北偏东15°的方向上.
19.解:由题意可知△BMP为直角三角形,BM=8×2=16(海里),BP=15×2=30(海里),∴MP==34海里.
答:P岛与M岛之间的距离为34海里.
20.解:如图,过B点作BM⊥FD于点M.
INCLUDEPICTURE"F15.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\F15.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\F15.tif" \* MERGEFORMATINET
在△ACB中,
∵∠ACB=90°,∠A=60°,
∴∠ABC=30°,∴AB=2AC=20,
∴BC===10.
∵AB∥CF,∴∠BCM=∠ABC=30°,
∴BM=BC=5,
∴CM===15.
在△EFD中,
∵∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5,
∴CD=CM-MD=15-5.
21.解:(1)锐角;钝角
(2)>;<
(3)∵c为最长边长,2+4=6,
∴4<c<6.a2+b2=22+42=20.
①当a2+b2>c2,即c2<20时,4<c<2,
∴当4<c<2时,这个三角形是锐角三角形;
②当a2+b2=c2,即c2=20时,c=2,
∴当c=2时,这个三角形是直角三角形;
③当a2+b2<c2,即c2>20时,2∴当2<c<6时,这个三角形是钝角三角形.
22.解:(1)(3,4);(0,1)
(2)点E能恰好落在x轴上.
∵四边形OABC为长方形,
∴BC=OA=4,∠AOC=∠DCO=90°,
由折叠的性质可得DE=BD=BC-CD=4-1=3,AE=AB=OC=m.
如图,假设点E恰好落在x轴上.
在Rt△CDE中,
由勾股定理可得EC===2,
则有OE=OC-CE=m-2.
在Rt△AOE中,OA2+OE2=AE2,
即42+(m-2)2=m2,
解得m=3.
一、选择题(每题3分,共30分)
1.在Rt△AOB中,∠AOB=90°,若AB=10,AO=6,则OB的长为( )
A.5 B.6 C.8 D.10
2.下列四组数中不能构成直角三角形三边长的一组是( )
A.1,2, B.3,5,4 C.5,12,13 D.4,13,15
3.直角三角形的一条直角边长是另一条直角边长的,斜边长为10,则它的面积为( )
A.10 B.15 C.20 D.30
4.如图,P是第一象限的平分线上一点,且OP=2,则P点的坐标为( )
A.(2,2)
B.(,)
C.(2,)
D.(,2)
5.若等腰直角三角形斜边上的高为1,则它的周长是( )
A.4 B.2+1 C.4 D.2+2
6.下列各组数是勾股数的是( )
A.6,7,8 B.1,,2 C.5,4,3 D.0.3,0.4,0.5
7.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三边长分别为5里,12里,13里,问这块沙田面积有多大?题中1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米
C.75平方千米 D.750平方千米
8.在△ABC中,AC=9,BC=12,AB=15,则AB边上的高是( )
A. B. C. D.
9.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线上D′处.若AB=3,AD=4,则ED的长为( )
A. B.3 C.1 D.
10.四个全等的直角三角形按如图的方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长的直角边,若AM=2EF,则正方形ABCD的面积为( )
A.14S B.13S C.12S D.11S
二、填空题(每题3分,共18分)
11.在平面直角坐标系中,点A(-3,0)与点B(0,2)的距离是__________.
12.若直角三角形的两直角边长分别为a,b,且满足a2-6a+9+|b-4|=0,则该直角三角形的斜边长为__________.
13.如图,从点A(0,2)发出的一束光,经x轴反射后,过点B(4,3),则这束光从点A到点B所经过路径的长为________.
14.如图,在三角形ABC中,AC=3,BC=4,AB=5,P为直线AB上一动点,连接PC,则线段PC的最小值是__________.
15.我国古代数学名著《九章算术》中有云:“今有木长二丈,围之三尺,葛生其下,缠木七周,上与木齐,问葛长几何?”大意:有一根木头长2丈,上、下底面的周长为3尺,葛藤生长在木下的A点,绕木7周,葛梢与木头上端B点刚好齐平(如图).则葛长是________尺.(注:1丈等于10尺,葛缠木以最短的路径向上长,误差忽略不计)
16.如图,在△ABC中,AB=AC=10 cm,BC=16 cm,现点P从点B出发,沿BC向C点运动,运动速度为cm/s,若点P的运动时间为t s,则当△ABP是直角三角形时,t的值是________.
三、解答题(17~20题每题8分,21~22题每题10分,共52分)
17.在△ABC中,∠C=90°,AB=20,若∠A=60°,求BC,AC的长.
18.如图,一艘船由A港沿北偏东60°方向航行10 km至B港,然后再沿北偏西30°方向航行10 km至C港.
(1)求A,C两港之间的距离(结果保留到0.1 km,参考数据:≈1.414,≈1.732);
(2)确定C港在A港的什么方向.
INCLUDEPICTURE"HKJJJ26.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\HKJJJ26.tif" \* MERGEFORMATINET
19.如图,在B港有甲、乙两艘渔船,若甲渔船沿北偏东60°方向以每小时8海里的速度前进,乙渔船沿南偏东30°方向以每小时15海里的速度前进,两小时后,甲船到达M岛,乙船到达P岛.求P岛与M岛之间的距离.
INCLUDEPICTURE"8SXHK59.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\8SXHK59.tif" \* MERGEFORMATINET
20.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
INCLUDEPICTURE"F10.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\F10.tif" \* MERGEFORMATINET
21.在△ABC中,BC=a,AC=b,AB=c,设c为最长边长,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边长分别为6,8,9时,△ABC为________三角形;当△ABC三边长分别为6,8,11时,△ABC为________三角形.
(2)猜想:当a2+b2________c2时,△ABC为锐角三角形;当a2+b2________c2时,△ABC为钝角三角形.
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
22.如图,将长方形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将长方形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当m=3时,点B的坐标为________,点E的坐标为________;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
INCLUDEPICTURE"i71.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\i71.tif" \* MERGEFORMATINET
答案
一、1.C 2.D
3.B 点拨:设较短直角边长为x(x>0),则有x2+(3x)2=102,解得x=,∴直角三角形的面积S=x·3x=15.
4.B 5.D 6.C
7.A 点拨:由题意可得三角形沙田的三边长为2.5千米,6千米,6.5千米.因为2.52+62=6.52,所以这个三角形为直角三角形,直角边长为2.5千米和6千米,所以S=×6×2.5=7.5(平方千米),故选A.
8.A
9.A 点拨:在Rt△ABC中,AC===5.设ED=x,则D′E=x,AE=4-x,在Rt△AD′E中,AD′=AC-CD′=2,根据勾股定理可得方程22+x2=(4-x)2,再解方程即可.
10.B 点拨:设AM=2a,BM=b,则正方形ABCD的面积=4a2+b2.
由题意知EF=(2a-b)-2(a-b)=2a-b-2a+2b=b.
∵AM=2EF,∴2a=2b,
∴a=b.
∵正方形EFGH的面积为S,
∴b2=S,
∴正方形ABCD的面积=4a2+b2=13b2=13S.故选B.
二、11.
12.5 点拨:∵a2-6a+9+|b-4|=0,∴(a-3)2+|b-4|=0,∴a-3=0,b-4=0,解得a=3,b=4,
∴该直角三角形的斜边长===5.
13. 14. 15.29
16.32或50 点拨:如图①,当∠APB=90°时,AP⊥BC,∵AB=AC,AP⊥BC,∴BP=CP=BC=8 cm,∴t=8,解得t=32;如图②,当∠PAB=90°时,过点A作AE⊥BC于点E.
∵AB=AC,AE⊥BC,∴BE=CE=BC=8 cm,∴PE=BP-BE=cm.在Rt△AEC中,AE2=AC2-CE2,即AE2=102-82,解得AE=6 cm,在Rt△PAB中,AP2=BP2-AB2,在Rt△AEP中,AP2=PE2+AE2,
∴-100=+36,解得t=50.综上所述,t的值为32或50.
INCLUDEPICTURE"8SXHK74.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\8SXHK74.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\8SXHK74.tif" \* MERGEFORMATINET
三、17.解:∵∠C=90°,∠A=60°,
∴∠B=180°-∠C-∠A=180°-90°-60°=30°.
∴AC=AB=×20=10.
在Rt△ABC中,由勾股定理得BC===10.
18.解:(1)由题意得∠PBC=30°,∠MAB=60°,
∴∠CBQ=60°,∠BAN=30°,
∴∠ABQ=30°,∴∠ABC=90°.
∵AB=BC=10,
∴AC==10≈14.1.
答:A、C两港之间的距离约为14.1 km.
(2)由(1)知,△ABC为等腰直角三角形,
∴∠BAC=45°,∴∠CAM=60°-45°=15°,
∴C港在A港北偏东15°的方向上.
19.解:由题意可知△BMP为直角三角形,BM=8×2=16(海里),BP=15×2=30(海里),∴MP==34海里.
答:P岛与M岛之间的距离为34海里.
20.解:如图,过B点作BM⊥FD于点M.
INCLUDEPICTURE"F15.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\F15.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\F15.tif" \* MERGEFORMATINET
在△ACB中,
∵∠ACB=90°,∠A=60°,
∴∠ABC=30°,∴AB=2AC=20,
∴BC===10.
∵AB∥CF,∴∠BCM=∠ABC=30°,
∴BM=BC=5,
∴CM===15.
在△EFD中,
∵∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5,
∴CD=CM-MD=15-5.
21.解:(1)锐角;钝角
(2)>;<
(3)∵c为最长边长,2+4=6,
∴4<c<6.a2+b2=22+42=20.
①当a2+b2>c2,即c2<20时,4<c<2,
∴当4<c<2时,这个三角形是锐角三角形;
②当a2+b2=c2,即c2=20时,c=2,
∴当c=2时,这个三角形是直角三角形;
③当a2+b2<c2,即c2>20时,2
22.解:(1)(3,4);(0,1)
(2)点E能恰好落在x轴上.
∵四边形OABC为长方形,
∴BC=OA=4,∠AOC=∠DCO=90°,
由折叠的性质可得DE=BD=BC-CD=4-1=3,AE=AB=OC=m.
如图,假设点E恰好落在x轴上.
在Rt△CDE中,
由勾股定理可得EC===2,
则有OE=OC-CE=m-2.
在Rt△AOE中,OA2+OE2=AE2,
即42+(m-2)2=m2,
解得m=3.
