沪科版八下数学第20章数据的初步分析达标测试卷(含答案)
文档属性
| 名称 | 沪科版八下数学第20章数据的初步分析达标测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 121.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-17 19:50:33 | ||
图片预览

文档简介
第20章达标测试卷
一、选择题(每题3分,共30分)
1.如果一组数据-3,-2,0,1,x,6,9,12的平均数为3,则x为( )
A.2 B.3 C.-1 D.1
2.一组数据:1,2,4,2,2,5,这组数据的众数是( )
A.1 B.2 C.4 D.5
3.每年的3月12日是我国的植树节,某学校在“爱护地球,绿化祖国”的活动中,组织了100名学生开展植树造林活动,其植树情况整理如下表,则这100名学生植树棵数的中位数为( )
植树棵数 4 5 6 7 9
人数 30 20 27 15 8
A.4 B.5 C.5.5 D.6
4.明明开车从甲地前往乙地,途中加了几次油,行驶的路程与耗油量如下表所示,则汽车每行驶1百公里的平均耗油量为( )
行驶路程/百公里 5 4.8 4 5
耗油量/升 45 40.8 40.4 43
A.9升 B.8.8升 C.9.5升 D.8升
5.某区“引进人才”招聘考试分笔试和面试.其中笔试按60%、面试按40%计算加权平均数作为总成绩.吴老师笔试成绩为90分,面试成绩为85分,那么吴老师的总成绩为( )
A.85分 B.86分 C.87分 D.88分
6.受央视《朗读者》节目的启发的影响,某校七年级(2)班近期准备组织一次朗诵活动,语文老师调查了全班学生平均每天的阅读时间,统计结果如下表所示,则在本次调查中,全班学生平均每天阅读时间的中位数和众数分别是( )
平均每天阅读时间/小时 0.5 1 1.5 2
人数 8 19 10 3
A.2小时,1小时 B.1小时,1.5小时
C.1小时,2小时 D.1小时,1小时
7.甲、乙、丙、丁四名射击运动员参加射击预选赛,他们射击成绩的平均环数x及方差s2如下表所示:
甲 乙 丙 丁
x 8 9 9 8
s2 1.2 1 1.2 1
若要选出一个成绩较好状态稳定的运动员去参赛,那么应选运动员( )
A.甲 B.乙 C.丙 D.丁
8.把一组数据中的每一个数据都减去80,得到一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( )
A.78.8,75.6 B.78.8,4.4 C.81.2,84.4 D.81.2,4.4
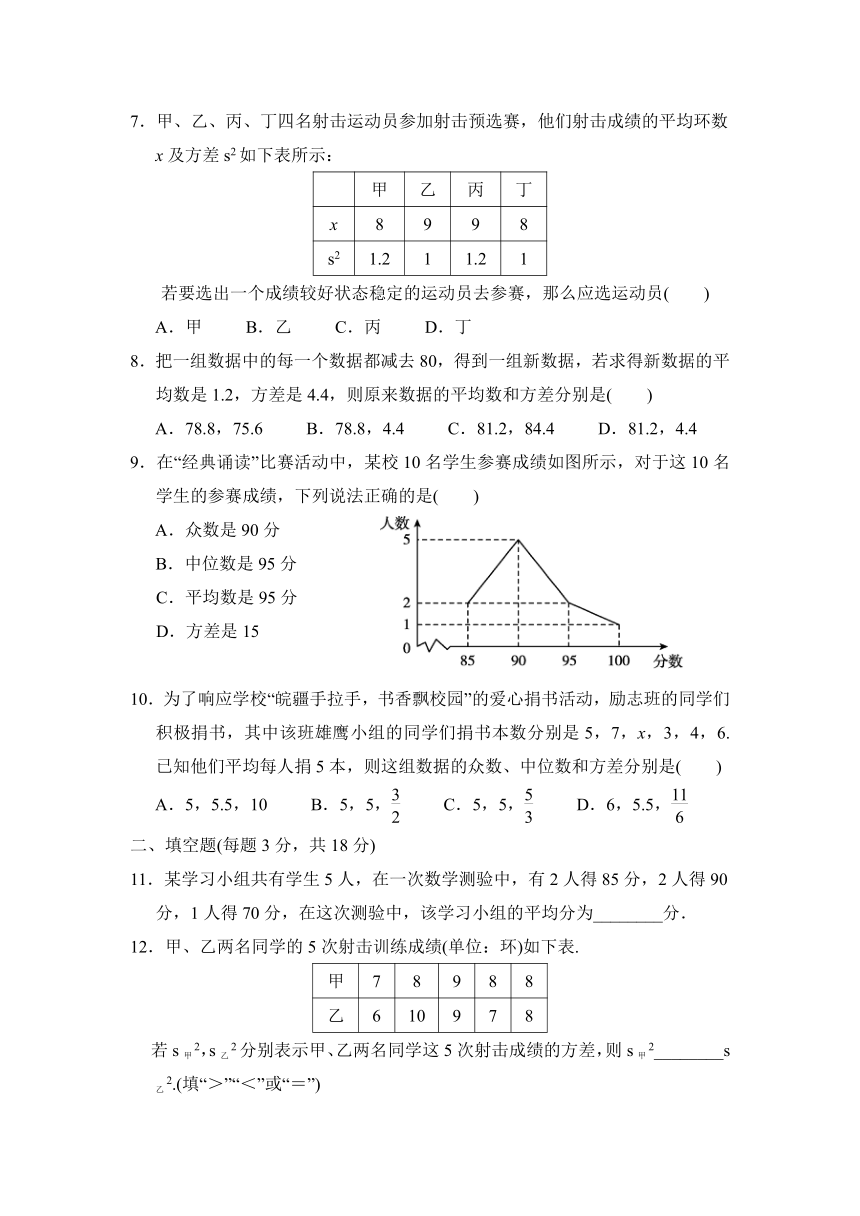
9.在“经典诵读”比赛活动中,某校10名学生参赛成绩如图所示,对于这10名学生的参赛成绩,下列说法正确的是( )
A.众数是90分
B.中位数是95分
C.平均数是95分
D.方差是15
10.为了响应学校“皖疆手拉手,书香飘校园”的爱心捐书活动,励志班的同学们积极捐书,其中该班雄鹰小组的同学们捐书本数分别是5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是( )
A.5,5.5,10 B.5,5, C.5,5, D.6,5.5,
二、填空题(每题3分,共18分)
11.某学习小组共有学生5人,在一次数学测验中,有2人得85分,2人得90分,1人得70分,在这次测验中,该学习小组的平均分为________分.
12.甲、乙两名同学的5次射击训练成绩(单位:环)如下表.
甲 7 8 9 8 8
乙 6 10 9 7 8
若s甲2,s乙2分别表示甲、乙两名同学这5次射击成绩的方差,则s甲2________s乙2.(填“>”“<”或“=”)
13.一组数据:1,2,3,4,x,其中位数与平均数相同,则x的值为________.
14.为了估计某鱼塘里鱼的条数,先捕捞30条鱼,给它们分别做上标记,然后放回鱼塘中,待有标记的鱼完全混合于鱼群后,再捕捞出80条鱼,发现其中2条有标记,从而估计这个鱼塘中有鱼__________条.
15.已知一组数据x1,x2,x3的平均数和方差分别是2,,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是________.
16.数据1,3,5,12,a,其中整数a是这组数据的中位数,则该组数据的平均数是__________.
三、解答题(17~20题每题8分,21~22题每题10分,共52分)
17.在“心系灾区”自愿捐款活动中,某班30名同学的捐款情况如下表:
捐款数/元 5 10 15 20 25 30
人数 11 9 6 2 1 1
(1)这个班捐款总数是多少元?
(2)求这30名同学捐款的平均数.
18.为了宣传节约用水,小明随机调查了某小区家庭5月份的用水情况,并将收集的数据整理成如图所示的统计图.
(1)小明一共调查了多少户家庭?
(2)求所调查家庭5月份用水量的众数和平均数;
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.
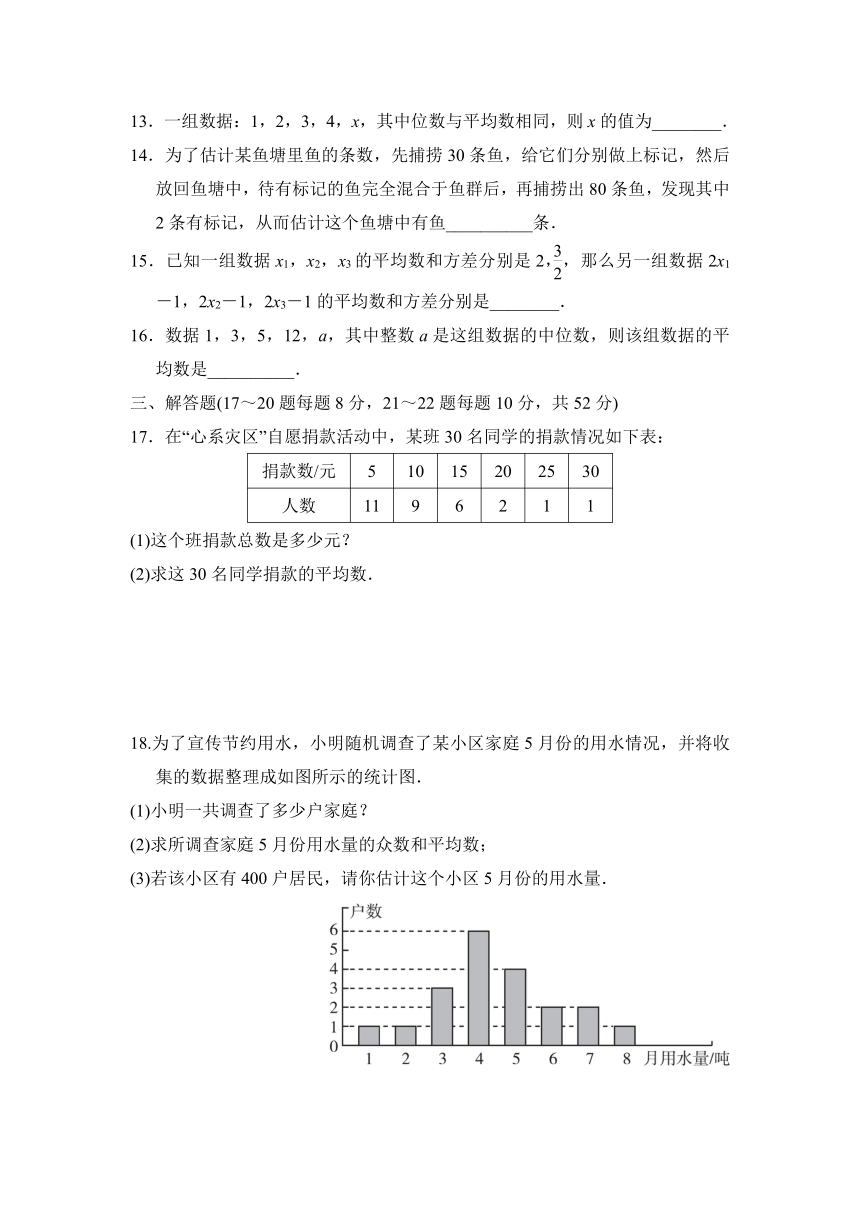
19.某班对最近一次数学测验成绩(得分取整数)进行统计分析,将所有成绩由低到高分成五组,并绘制成如图所示的频数直方图,请结合直方图提供的信息,回答下列问题:
(1)该班共有________名同学参加这次测验;
(2)这次测验成绩的中位数落在哪个分数段内?
(3)若这次测验中,成绩在80分以上(不含80分)为优秀,则该班这次数学测验的优秀率是多少?
INCLUDEPICTURE"XJ9.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\XJ9.tif" \* MERGEFORMATINET
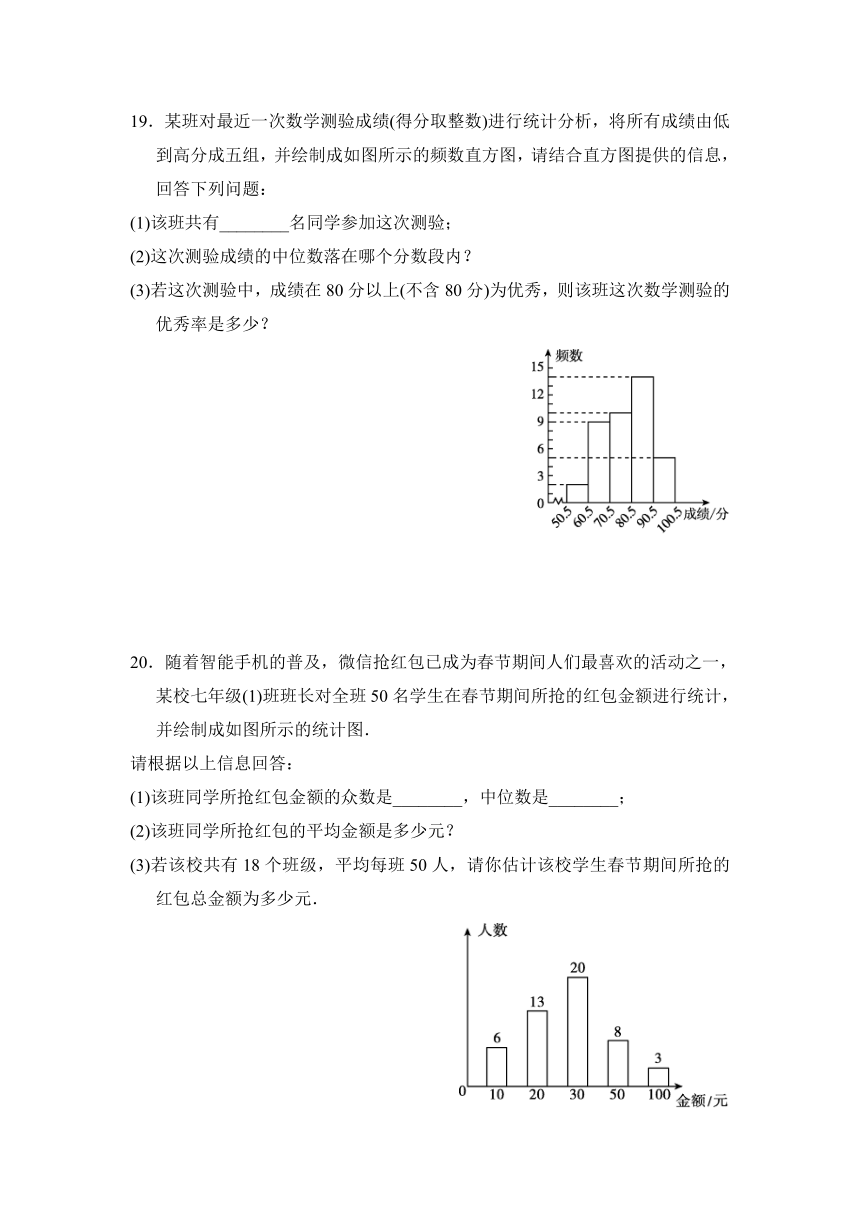
20.随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(1)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成如图所示的统计图.
请根据以上信息回答:
(1)该班同学所抢红包金额的众数是________,中位数是________;
(2)该班同学所抢红包的平均金额是多少元?
(3)若该校共有18个班级,平均每班50人,请你估计该校学生春节期间所抢的红包总金额为多少元.
INCLUDEPICTURE"YH136.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\YH136.tif" \* MERGEFORMATINET
21.张军和李斌两名同学报名参加了校短跑训练小组,如图记录了他们近5次百米训练中所测得的成绩.
INCLUDEPICTURE"DX5.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\DX5.tif" \* MERGEFORMATINET
请根据图中所给的信息,解答下列问题:
(1)根据图中的信息,补全下面的表格(单位:秒):
第1次 第2次 第3次 第4次 第5次
张军 13.3 13.4 13.3 13.3
李斌 13.2 13.1 13.5 13.3
(2)直接写出他们成绩的平均数和方差;
(3)若你是他们的教练,比较张军与李斌的成绩后,你将分别给予他们怎样的建议?
22.为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩,数据如下(单位:分):
90 91 89 96 90 98 90 97 91 98
99 97 91 88 90 97 95 90 95 88
(1)根据上述数据,将下列表格补充完整.
平均数/分 众数/分 中位数/分
93 ________ 91
(2)根据所给数据,如果该校想确定七年级前50%的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为________分;
(3)根据数据分析,该校决定在七年级授予测评成绩前30%的学生“禁毒小卫士”荣誉称号,请估计评选该荣誉称号的最低分数,并说明理由.
答案
一、1.D 2.B 3.C 4.A 5.D
6.D 7.B
8.D 点拨:原来数据的平均数是80+1.2=81.2,方差是4.4.
9.A
10.C 点拨:由题意知,5,7,x,3,4,6的平均数为5,所以x=5.所以众数是5,中位数是5,方差是×[(7-5)2+(6-5)2+2×(5-5)2+(4-5)2+(3-5)2]=.故选C.
二、11.84 12.< 13.0或2.5或5
14.1 200 点拨:设该鱼塘有鱼x条,根据题意得=,
解得x=1 200.
经检验x=1 200是原分式方程的解,
即估计该鱼塘有鱼1 200条.
15.3,6
16.4.8或5或5.2
三、17.解:(1)5×11+10×9+15×6+20×2+25×1+30×1=330(元).
答:这个班捐款总数是330元.
(2)330÷30=11(元)
答:这30名同学捐款的平均数是11元.
18.解:(1)1+1+3+6+4+2+2+1=20(户).
答:小明一共调查了20户家庭.
(2)平均数为=4.5(吨),众数是4吨.
(3)4.5×400=1 800(吨).
答:估计这个小区5月份的用水量约为1 800吨.
19.解:(1)40
(2)这次测验成绩的中位数落在分数段70.5~80.5分内.
(3)×100%=47.5%.
答:该班这次数学测验的优秀率是47.5%.
20.解:(1)30元;30元
(2)该班同学所抢红包的平均金额是(6×10+13×20+20×30+8×50+3×100)÷50=32.4(元).
(3)18×50×32.4=29 160(元).
答:估计该校学生春节期间所抢的红包总金额为29 160元.
21.解:(1)从上到下依次填:13.2;13.4
(2)张军成绩的平均数是13.3秒,李斌成绩的平均数是13.3秒;张军成绩的方差是0.004,李斌成绩的方差是0.02.
(3)张军的成绩虽然较稳定,但缺少较好成绩,需要通过训练使成绩更好;在两人的最好成绩中,李斌比张军的最好成绩要好,但稳定性不够,需要通过不断训练加强成绩的稳定性.
22. 解:(1)90
(2)91
(3)估计评选该荣誉称号的最低分数为97分. 理由如下:
∵20×30%=6,∴估计评选该荣誉称号的最低分数为97分.
一、选择题(每题3分,共30分)
1.如果一组数据-3,-2,0,1,x,6,9,12的平均数为3,则x为( )
A.2 B.3 C.-1 D.1
2.一组数据:1,2,4,2,2,5,这组数据的众数是( )
A.1 B.2 C.4 D.5
3.每年的3月12日是我国的植树节,某学校在“爱护地球,绿化祖国”的活动中,组织了100名学生开展植树造林活动,其植树情况整理如下表,则这100名学生植树棵数的中位数为( )
植树棵数 4 5 6 7 9
人数 30 20 27 15 8
A.4 B.5 C.5.5 D.6
4.明明开车从甲地前往乙地,途中加了几次油,行驶的路程与耗油量如下表所示,则汽车每行驶1百公里的平均耗油量为( )
行驶路程/百公里 5 4.8 4 5
耗油量/升 45 40.8 40.4 43
A.9升 B.8.8升 C.9.5升 D.8升
5.某区“引进人才”招聘考试分笔试和面试.其中笔试按60%、面试按40%计算加权平均数作为总成绩.吴老师笔试成绩为90分,面试成绩为85分,那么吴老师的总成绩为( )
A.85分 B.86分 C.87分 D.88分
6.受央视《朗读者》节目的启发的影响,某校七年级(2)班近期准备组织一次朗诵活动,语文老师调查了全班学生平均每天的阅读时间,统计结果如下表所示,则在本次调查中,全班学生平均每天阅读时间的中位数和众数分别是( )
平均每天阅读时间/小时 0.5 1 1.5 2
人数 8 19 10 3
A.2小时,1小时 B.1小时,1.5小时
C.1小时,2小时 D.1小时,1小时
7.甲、乙、丙、丁四名射击运动员参加射击预选赛,他们射击成绩的平均环数x及方差s2如下表所示:
甲 乙 丙 丁
x 8 9 9 8
s2 1.2 1 1.2 1
若要选出一个成绩较好状态稳定的运动员去参赛,那么应选运动员( )
A.甲 B.乙 C.丙 D.丁
8.把一组数据中的每一个数据都减去80,得到一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( )
A.78.8,75.6 B.78.8,4.4 C.81.2,84.4 D.81.2,4.4
9.在“经典诵读”比赛活动中,某校10名学生参赛成绩如图所示,对于这10名学生的参赛成绩,下列说法正确的是( )
A.众数是90分
B.中位数是95分
C.平均数是95分
D.方差是15
10.为了响应学校“皖疆手拉手,书香飘校园”的爱心捐书活动,励志班的同学们积极捐书,其中该班雄鹰小组的同学们捐书本数分别是5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是( )
A.5,5.5,10 B.5,5, C.5,5, D.6,5.5,
二、填空题(每题3分,共18分)
11.某学习小组共有学生5人,在一次数学测验中,有2人得85分,2人得90分,1人得70分,在这次测验中,该学习小组的平均分为________分.
12.甲、乙两名同学的5次射击训练成绩(单位:环)如下表.
甲 7 8 9 8 8
乙 6 10 9 7 8
若s甲2,s乙2分别表示甲、乙两名同学这5次射击成绩的方差,则s甲2________s乙2.(填“>”“<”或“=”)
13.一组数据:1,2,3,4,x,其中位数与平均数相同,则x的值为________.
14.为了估计某鱼塘里鱼的条数,先捕捞30条鱼,给它们分别做上标记,然后放回鱼塘中,待有标记的鱼完全混合于鱼群后,再捕捞出80条鱼,发现其中2条有标记,从而估计这个鱼塘中有鱼__________条.
15.已知一组数据x1,x2,x3的平均数和方差分别是2,,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是________.
16.数据1,3,5,12,a,其中整数a是这组数据的中位数,则该组数据的平均数是__________.
三、解答题(17~20题每题8分,21~22题每题10分,共52分)
17.在“心系灾区”自愿捐款活动中,某班30名同学的捐款情况如下表:
捐款数/元 5 10 15 20 25 30
人数 11 9 6 2 1 1
(1)这个班捐款总数是多少元?
(2)求这30名同学捐款的平均数.
18.为了宣传节约用水,小明随机调查了某小区家庭5月份的用水情况,并将收集的数据整理成如图所示的统计图.
(1)小明一共调查了多少户家庭?
(2)求所调查家庭5月份用水量的众数和平均数;
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.
19.某班对最近一次数学测验成绩(得分取整数)进行统计分析,将所有成绩由低到高分成五组,并绘制成如图所示的频数直方图,请结合直方图提供的信息,回答下列问题:
(1)该班共有________名同学参加这次测验;
(2)这次测验成绩的中位数落在哪个分数段内?
(3)若这次测验中,成绩在80分以上(不含80分)为优秀,则该班这次数学测验的优秀率是多少?
INCLUDEPICTURE"XJ9.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\XJ9.tif" \* MERGEFORMATINET
20.随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(1)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成如图所示的统计图.
请根据以上信息回答:
(1)该班同学所抢红包金额的众数是________,中位数是________;
(2)该班同学所抢红包的平均金额是多少元?
(3)若该校共有18个班级,平均每班50人,请你估计该校学生春节期间所抢的红包总金额为多少元.
INCLUDEPICTURE"YH136.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\YH136.tif" \* MERGEFORMATINET
21.张军和李斌两名同学报名参加了校短跑训练小组,如图记录了他们近5次百米训练中所测得的成绩.
INCLUDEPICTURE"DX5.tif" INCLUDEPICTURE "F:\\20春初中\\数学\\8HK\\word\\DX5.tif" \* MERGEFORMATINET
请根据图中所给的信息,解答下列问题:
(1)根据图中的信息,补全下面的表格(单位:秒):
第1次 第2次 第3次 第4次 第5次
张军 13.3 13.4 13.3 13.3
李斌 13.2 13.1 13.5 13.3
(2)直接写出他们成绩的平均数和方差;
(3)若你是他们的教练,比较张军与李斌的成绩后,你将分别给予他们怎样的建议?
22.为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩,数据如下(单位:分):
90 91 89 96 90 98 90 97 91 98
99 97 91 88 90 97 95 90 95 88
(1)根据上述数据,将下列表格补充完整.
平均数/分 众数/分 中位数/分
93 ________ 91
(2)根据所给数据,如果该校想确定七年级前50%的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为________分;
(3)根据数据分析,该校决定在七年级授予测评成绩前30%的学生“禁毒小卫士”荣誉称号,请估计评选该荣誉称号的最低分数,并说明理由.
答案
一、1.D 2.B 3.C 4.A 5.D
6.D 7.B
8.D 点拨:原来数据的平均数是80+1.2=81.2,方差是4.4.
9.A
10.C 点拨:由题意知,5,7,x,3,4,6的平均数为5,所以x=5.所以众数是5,中位数是5,方差是×[(7-5)2+(6-5)2+2×(5-5)2+(4-5)2+(3-5)2]=.故选C.
二、11.84 12.< 13.0或2.5或5
14.1 200 点拨:设该鱼塘有鱼x条,根据题意得=,
解得x=1 200.
经检验x=1 200是原分式方程的解,
即估计该鱼塘有鱼1 200条.
15.3,6
16.4.8或5或5.2
三、17.解:(1)5×11+10×9+15×6+20×2+25×1+30×1=330(元).
答:这个班捐款总数是330元.
(2)330÷30=11(元)
答:这30名同学捐款的平均数是11元.
18.解:(1)1+1+3+6+4+2+2+1=20(户).
答:小明一共调查了20户家庭.
(2)平均数为=4.5(吨),众数是4吨.
(3)4.5×400=1 800(吨).
答:估计这个小区5月份的用水量约为1 800吨.
19.解:(1)40
(2)这次测验成绩的中位数落在分数段70.5~80.5分内.
(3)×100%=47.5%.
答:该班这次数学测验的优秀率是47.5%.
20.解:(1)30元;30元
(2)该班同学所抢红包的平均金额是(6×10+13×20+20×30+8×50+3×100)÷50=32.4(元).
(3)18×50×32.4=29 160(元).
答:估计该校学生春节期间所抢的红包总金额为29 160元.
21.解:(1)从上到下依次填:13.2;13.4
(2)张军成绩的平均数是13.3秒,李斌成绩的平均数是13.3秒;张军成绩的方差是0.004,李斌成绩的方差是0.02.
(3)张军的成绩虽然较稳定,但缺少较好成绩,需要通过训练使成绩更好;在两人的最好成绩中,李斌比张军的最好成绩要好,但稳定性不够,需要通过不断训练加强成绩的稳定性.
22. 解:(1)90
(2)91
(3)估计评选该荣誉称号的最低分数为97分. 理由如下:
∵20×30%=6,∴估计评选该荣誉称号的最低分数为97分.
